40.Теплообмен при свободной конвекции у вертикальной плиты

В этом случае жидкая или газообразная среда простирается в бесконечность по нормали к поверхности внесенного в нее твердого тела.

При термической свободной конвекции у вертикальной поверхности нагретого тела (), начиная от нижней кромки, течение в пограничном слое сначала ламинарно.

На некотором расстоянии от нижней кромки толщина ламинарного пограничного слоя становится большой, его устойчивость потока теряется и течение в пограничном слое становится локонообразным. Еще выше оно становится турбулентным

Интенсивность теплообмена на выделенном участке плиты зависит от того, какова протяженность находящегося на нем ламинарного, локонообразного или турбулентного течений. Критериальные формулы для описания теплообмена при свободной конвекции должны иметь вид связи между числом Нуссельта и критерием Рэлея

41.Третья (основная) теорема теории подобия и моделирования физических явлений

Для подобия двух явлений одинаковой физической природы необходимо подобие распределений, соответствующих условиям однозначности решения исследуемой краевой задачи, т.е. необходимо подобие геометрических областей, свойств среды, начальных и граничных распределений искомых величин, и достаточно равенства одноименных критериев подобия, составленных для сравниваемых явлений.

Ее сформулировали отечественные ученые акад. М.В. Кирпичев и проф. А.А. Гухман, и она названа в их честь теоремой Кирпичева–Гухмана.

42.47.Вывод аргумента Ra для описания теплоотдачи при свободной конвекции

следствием подобия температурных распределений в «натуре» и «модели» является равенство составленных для них чисел Нуссельта. Достаточным же условием для этого подобия при вынужденном движении является равенство критериев Рейнольдса и Пекле.

Достаточным условием для подобия температурных полей при термической свободной конвекции является равенство безразмерных комплексов и критериев Пекле.

.

При термической свободной конвекции неизвестна характерная скорость w₀. Чтобы ее исключить, умножим друг на друга аргументы для числа Нуссельта:

Получившийся при этом безразмерный комплекс составлен из величин, заданных при постановке задачи о развитии процесса свободной конвекции. Он называется критерием Рэлея и обозначается Ra в честь выдающегося физика:

Таким образом, для термической свободной конвекции равенство критериев Рэлея приводит к равенству чисел Нуссельта, так что справедлива зависимость

Nu = f(Ra).

43.Вывод критериев подобия из рассмотрения уравнения нестационарного теплопереноса в потоке (уравнения Фурье-Кирхгофа)

Для вынужденного обтекания потоком пластины или при его течении в прямолинейном канале постоянного поперечного сечения влияние градиента давления отсутствует или незначительно и развитие процесса (формирование распределения скорости) определяется отношением силы инерции к силе вязкостного трения .

оператор (grad):

Мера отношения обозначается как

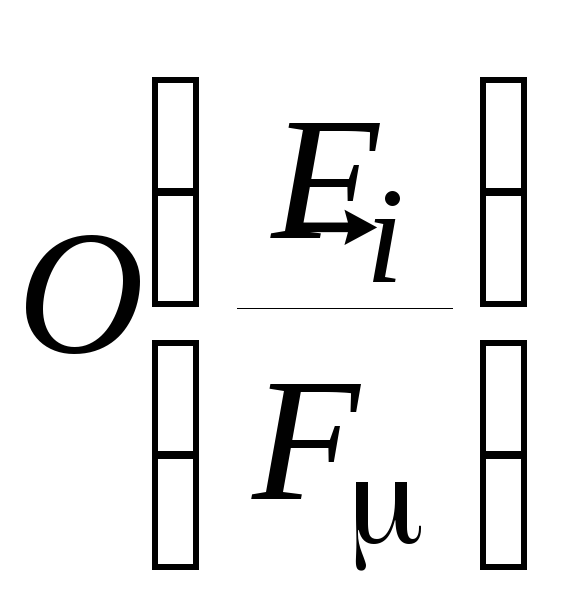
Назначим в качестве меры для известную скорость потока w₀ на входе в трубу, а в качестве меры для протяженностей x, y, z - ее диаметр d.

Безразмерный комплекс в правой части является мерой отношения силы инерции к силе вязкостного трения, его величина определяет характер вынужденного течения жидкости (газа). Он называется критерием Рейнольдса и обозначается Re

или

где  = / - коэффициент кинематической вязкости.

Для подобия распределения скоростей в двух безградиентных вынужденных течениях в каналах достаточно, чтобы выполнялось равенство критериев Рейнольдса, составленных для «натуры» и «модели»:

или

Достаточное условие подобия двух вынужденных течений в более общем виде:

Для подобия температурных полей прежде всего необходимо достаточное условие (при вынужденном движении равенство вычисленных для “натуры” и “модели” критериев Рейнольдса , при термическом свободном движении – равенство безразмерных комплексов , а при гравитационно-вязкостном течении – равенство критерия Рейнольдса и безразмерного комплекса ).

Кроме того, для суждения о подобии температурных полей в двух сравниваемых вынужденных или термических свободных течениях достаточно, чтобы выполнялось равенство

Q_к -сумма количества тепла, вносимого и выносимого движущейся средой механизмом конвекции

Q_т- сумма количества тепла, которое вносится и выносится механизмом молекулярной теплопроводности .

Безразмерный комплекс в правой части является мерой отношения тепловых потоков, переносимых механизмом конвекции и теплопроводности, его величина определяет температурные поля в движущейся среде. Он называется критерием Пекле и обозначается Pe:

Для подобия распределения температуры в двух сравниваемых течениях достаточно, чтобы выполнялись равенства указанных выше безразмерных комплексов, обеспечивающих гидродинамическое подобие течений, и составленных для них критериев Пекле

Pe₁ = Pe₂ или .

Выполняя элементарные преобразования, получаем также

,

где безразмерное отношение называется критерием Прандтля и обозначается Pr