1.4. Уравнение Фурье

Напомним, что основной задачей теории теплопроводности является определение температуры в любой точке тела в любой момент времени от начала его нагревания или охлаждения, т.е. установление связи вида

, (1.8)

где .

Для этого необходимо решать так называемое уравнение Фурье (уравнение теплопроводности).

Уравнение Фурье первоначально установим для самого простого случая одномерного распространения тепла в пластине (рис. 1.3). Выделим двумя плоскостями, параллельными ограничивающим плоскостям тела, слой толщиной dx и рассмотрим прохождение тепла через единицу площади изотермической поверхности (рис. 1.4).

Рис. 1.4

Положим также, что в теле отсутствуют источники объемного тепловыделения, причиной которого может быть наличие химической реакции, ядерного распада, прохождение электрического тока и т.д.

Представляется очевидным, что если в выделенный слой, объем которого равен 1dx, тепла «втекает» больше, чем «вытекает» , то температура в нем во времени будет повышаться 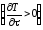. В противном случае температура понижается . В обоих случаях имеем процесс нестационарной теплопроводности.

Если же , то ясно, что температура в выделенном объеме тела во времени изменяться не будет и это соответствует процессу стационарной теплопроводности.

Пусть за время d температура в выделенном объеме изменится на величину dT, так что изменение внутренней энергии за единицу времени составляет

, (1.9)

где 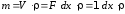– масса; c и  – удельная теплоемкость и плотность, так что имеем

. (1.9)

Знак частной производной в (1.9) использован потому, что температура T меняется не только во времени, но и в пространстве (в нашем случае она изменяется по координате x).

Единственной причиной изменения внутренней энергии во времени является разность «втекающего» q(x) и «вытекающего» q(x + dx) количества тепла, т.е. верно также равенство

. (1.10)

Разложим q(x + dx) в ряд Тейлора в окрестности точки с координатой x и ограничимся линейной частью разложения, тогда получим

и (1.10) примет вид

. (1.10)

Приравнивая правые части (1.9) и (1.10), получаем

. (1.11)

Таким образом, температура в том или ином месте пластины изменяется во времени лишь в том случае, когда изменяется от места к месту плотность теплового потока .

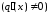На основании (1.3) имеем

так что уравнение (1.11) при  = const принимает вид

(1.11)

Это и есть уравнение Фурье, описывающее нестационарное одномерное (изменяющееся лишь по 0x) температурное поле в пластине.

В случае распространения тепла в прямолинейной призме (брусе) бесконечной длины и произвольной формы поперечного сечения с изотермической ограничивающей поверхностью достаточно рассмотреть распространение тепла в сечении, перпендикулярном оси призмы (рис. 1.2). Таким образом, мы приходим к понятию двухмерного температурного поля,

формирующегося в том случае, когда вектор плотности теплового потока «втекающего» и «вытекающего» в элементарный участок сечения призмы имеет ненулевые компоненты в направлениях 0x и 0y (рис. 1.5).

Рис. 1.5

Элементарный участок сечения призмы имеет вид прямоугольника и выделен плоскостями, отстоящими на x и x + dx, а также на y и y + dy от начала координат и имеет протяженность L в направлении 0z, перпендикулярном плоскости чертежа. В этом случае получаем последовательно

(1.12)

(1.13)

Далее, с учетом разложений

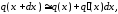
следует также

, (1.14)

и с привлечением (1.12) получаем

Наконец, учитывая, что при  = const

имеем в окончательном виде уравнение Фурье для описания двухмерного температурного поля

(1.15)

Нетрудно показать, что для самого общего случая объемного (трехмерного) температурного поля уравнение Фурье таково:

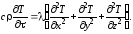(1.16)

Обратим внимание на то, что формулы (1.11), (1.15), (1.16) получены в предположении того, что теплофизические характеристики материала тела c, ,  неизменны. Уравнению (1.16) можно придать компактный вид

(1.16)

где – коэффициент температуропроводности материала тела; – оператор Лапласа; div – оператор дивергенции.

Уравнение Фурье представляет собой математическую запись закона сохранения энергии для ее тепловой формы, конкретный вид которой обусловлен использованием гипотезы Фурье .

В настоящее время справедливость этой гипотезы на основании результатов многочисленных приложений не вызывает сомнений, так что во многих работах эту гипотезу называют законом Фурье.

В математике (раздел «Математическая физика») уравнение (1.16) по ряду признаков отнесено к уравнению параболического типа и исследуются свойства его решения.

Отметим также, что для одномерного распространения тепла в пластине, цилиндре и шаре, когда их ограничивающие поверхности изотермичны, уравнение (1.16) принимает вид

(1.16)

где x – координата, отсчитанная от одной из плоскостей пластины, от оси цилиндра или от центра шара; s – коэффициент формы тела, равный единице, двум и трем для пластины, цилиндра и шара соответственно.

В заключение отметим, что для практически важного случая зависимости теплофизических характеристик материала тела от температуры – – уравнения (1.16) и (1.16) неприменимы. Можно показать, что вместо них необходимо рассматривать соответственно зависимости

(1.17)

и

. (1.18)