2.4. Особенности формирования динамического и теплового пограничных слоев во внешней и внутренней задачах

2.4.1. Обтекание пластины (внешняя задача)

Внешнее вынужденное обтекание тел различной конфигурации характеризуется тем, что поток жидкости (газа) по нормали к омываемой поверхности простирается достаточно далеко от нее (теоретически в бесконечность). Хорошо изученными считаются гидродинамика и теплообмен при внешнем обтекании пластины и одиночного цилиндра. Рассмотрим, как на поверхности обтекаемой пластины формируется динамический и тепловой пограничные слои.

Рис. 2.5

Пусть у передней кромки пластины x = 0 профиль скоростей равномерный, т.е. в каждой точке пространства над пластиной в этом поперечном сечении скорость везде одинакова и равна скорости w_ набегающего потока (рис. 2.5, а).

В настоящее время общепринята так называемая «гипотеза прилипания», согласно которой ближайшие к поверхности тела молекулы жидкости (газа) прилипают к ней, их скорость становится равной нулю. Межмолекулярные силы способствуют тому, что более удаленные от поверхности слои потока испытывают тормозящее действие с ее стороны, так что их скорость и становится меньшей, чем w_ (рис. 2.5, б; 2.5, в). Чем дальше отстоит сечение потока от передней кромки, тем глубже в поток проникает тормозящее действие стенки и тем больше становится толщина динамического пограничного слоя . Под величиной  понимается такое расстояние по нормали к точке на обтекаемой поверхности, на котором скорость w мало отличается от скорости невозмущенной части течения w_ (точнее говоря, отличается на наперед заданную малую величину).

Нетрудно видеть, что во внешней задаче нет принципиальных ограничений на величину , она может стать сколь угодно большой.

Детальное рассмотрение внешнего обтекания пластины потоком жидкости (газа) показывает, что, начиная от передней кромки, сначала формируется ламинарный пограничный слой, который затем, ниже по течению, становится неустойчивым, «разваливается». При этом движение в пограничном слое, начиная с расстояния от передней кромки, равного , соответствует чередующимся во времени и в пространстве ламинарному и турбулентному течениям – так называемая, переходная область течения. За ней течение на пластине становится турбулентным (рис. 2.6). Для практических приложений переходная область течения условно стягивается в точку, и таким образом полагают, что на пластине имеются лишь участки ламинарного и турбулентного течений.

Самостоятельную задачу представляет определение критического расстояния от передней кромки пластины x_кр, начиная с которого ламинарный пограничный слой становится турбулентным.

Рис. 2.6

В настоящее время величина x_кр определяется из следующей экспериментально установленной зависимости для критерия Рейнольдса, имеющего x_кр в качестве определяющего размера:

(2.26)

откуда получаем

Если на пластину набегает детурбулизированный поток, то в формуле (2.26) следует принимать = 5. Если же поток, приближаясь к передней кромке пластины, «задирался» плохо обтекаемыми телами, турбулизировался, то следует полагать = 3.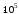

Имеются экспериментальные зависимости, позволяющие более точно указать величину в (2.26), однако для этого следует знать уровень турбулентности набегающего на пластину потока.

В гидромеханике установлено, что толщина ламинарного пограничного слоя равна

, (2.27)

а толщина турбулентного пограничного слоя в предположении, что участок ламинарного течения пренебрежимо мал, такова:

, (2.28)

где – значение критерия Рейнольдса, построенного по локальной координате точки на пластине.

Структура турбулентного пограничного слоя весьма сложна, и в настоящее время его условно разбивают на три участка (трехслойная модель Т. Кармана – В. Шваба), которые отличаются друг от друга относительной интенсивностью молекулярного и молярного (турбулентного) механизмов переноса количества движения, тепла, вещества и т.д.

В такой модели принимают, что в пристенном, вязком подслое, толщина которого определяется по формуле

, (2.29)

преобладает молекулярный механизм обменных процессов.

В буферном подслое, который является промежуточным между турбулентным ядром потока и вязким подслоем и толщина которого в сумме с толщиной с вязкого подслоя равна

, (2.30)

в основном преобладает молярный механизм переноса по сравнению с молекулярным.

В турбулентном же ядре потока интенсивность молекулярного переноса пренебрежимо мала.

Более естественным образом возникает понятие теплового пограничного слоя. Для этого рассмотрим обтекание пластины с одинаковой температурой поверхности T_W потоком жидкости (газа) с температурой в каждой точке сечения у передней кромки (рис. 2.7).

Рис. 2.7

По мере продвижения потока от передней кромки (x = 0) вглубь него проникает «холодящее» действие стенки, так как T_W < , и тем большей становится толщина теплового пограничного слоя _Т. Под величиной _T понимается такое расстояние по нормали к точке на обтекаемой поверхности, на котором температура мало отличается от температуры невозмущенной в тепловом отношении части течения (точнее говоря, отличается на наперед заданную малую величину).

Нетрудно видеть, что во внешней задаче нет принципиальных ограничений и на величину _Т: она может стать любой.

Толщина теплового пограничного слоя на участке ламинарного течения () определяется из формулы

. (2.31)

Толщина теплового турбулентного пограничного слоя совпадает с толщиной динамического турбулентного пограничного слоя при условии их формирования от передней кромки пластины. При этом в рамках его трехслойной модели толщина подслоя молекулярной теплопроводности (условно назовем его вязким тепловым подслоем) определяется как

. (2.32)

Из последних двух соотношений отчетливо выступает физический смысл критерия Прандтля – – как меры отношения толщин теплового и динамического пограничных слоев, так как ими определяется глубина проникновения в поток динамических и термических возмущений, которые характеризуются соответственно коэффициентами кинематической вязкости и температуропроводности .