1.9.5. Нелинейная стационарная теплопроводность
Выше была рассмотрена стационарная теплопроводность при = const. Реальные материалы характеризуются зависимостью коэффициента теплопроводности от температуры. Рассмотрим в качестве примера нелинейную стационарную теплопроводность в неограниченной пластине при ГУ-I (рис. 1.23) для трех видов материала: а) = const; б) растет с ростом температуры; в) убывает с ростом температуры.
Рис. 1.23
Для этих случаев зависимость (1.2) для расчета плотности теплового потока дает
(1.112)
Указанная величина q положительна (q > 0) и, пересекая изотермические поверхности пластины, везде одинакова.
Тогда имеем также из (1.112)
(1.113)
В диаграмме T-x (рис. 1.23) производная dT/dx численно равна тангенсу угла наклона касательной к любой линии, проходящей в ней.
При = const имеем на основании (1.113)
т.е. получаем линейное распределение температуры по толщине пластины (линия a).
При росте с увеличением температуры в тех местах пластины, где температура выше, будет соответственно меньше модуль производной dT/dx (линия б).
И, наконец, при уменьшении с ростом температуры распределение температуры будет соответствовать линии в.
Таким образом, в пластине, изготовленной из реального материала, распределение температуры по координате x является нелинейным.
Зависимость
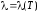влияет не только на вид стационарного
температурного поля: она приводит и к
необходимости учета этой зависимости
для подсчета количества тепла Q,
проходящего через тело.
Для рассмотренной выше неограниченной пластины при простейшей, линейной зависимости от температуры
(1.114)
вместо (1.52) имеем уже уравнение
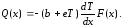(1.115)
Учитывая,
что в стационарном тепловом режиме
и для одномерного распространения тепла
в пластине
,
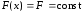приходим вместо (1.115) к уравнению
или
.
(1.116)
Полагая
известными температуры
и
,
получаем
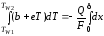и
.
(1.117)
Левая часть (1.117) приводится к следующему виду:
.
Нетрудно
видеть, что в соответствии с формулой
(1.114) второй сомножитель в правой части
последнего равенства представляет
собой коэффициент теплопроводности
материала
,
вычисленные по среднеарифметическому
значению температуры
.
Тогда вместо (1.117) получаем следующую
формулу для расчета количества тепла
Q, проходящего за
единицу времени через пластину:
.
2. Конвективный теплообмен
Для решения задач нестационарной и стационарной теплопроводности с граничными условиями третьего рода требуется знание коэффициента теплоотдачи . Формулы для его определения при различном характере теплового взаимодействия движущейся среды и обтекаемой поверхности твердого тела устанавливаются в настоящем разделе.
Помимо этого в некоторых случаях возникает необходимость и в определении температурных полей в потоке жидкости или газа.
Различают конвективный теплообмен при вынужденном и при свободном течении. В первом случае поток побуждается к движению насосами, вентиляторами, компрессорами и т.д.
Во
втором же случае движение жидкости или
газа возникает у поверхности теплого
или холодного тела, внесенного в их
объем. При наличии сил тяжести (сил
внешнего поля) у поверхности нагретого
тела возникает восходящий поток, а у
поверхности холодного тела - нисходящий
поток. Свободное движение в этом случае
называется термическим. Очевидно, что
оно будет продолжаться до тех пор, пока
имеется разность температур среды
и поверхности тела TW.
И при вынужденной, и при свободной
конвекции различают ламинарный,
переходной и турбулентный режимы
течения.
Не вдаваясь в детали, укажем на то, что при ламинарном движении поток «следует» руслу, элементарные струйки не перемешиваются друг с другом, так что перенос тепла от жидкости к омываемой поверхности (и наоборот) осуществляется лишь за счет хаотически движущихся молекул (атомов).
При турбулентном движении элементарные струйки жидкости перемешиваются, так что в потоке наряду с хаотически движущимися молекулами (атомами) хаотически движутся и турбулентные вихри, содержащие огромные количества молекул (атомов). Достигая, наряду с молекулами, обтекаемой поверхности, вихри отдают ей (или воспринимают от нее) тепло. Ясно, что конвективный теплообмен при турбулентном течении значительно интенсивнее, чем при ламинарном.
При переходном режиме течения в потоке одновременно существуют и чередуются во времени и пространстве участки ламинарного и турбулентного движения.