1. Теплопроводность

1.1. Механизм процесса

Механизм процесса обусловлен видом носителя тепла в твердых телах, жидкостях и газах.

В металлах электроны (электронный газ) при своем перемещении переносят не только электрический заряд, но и присущую им энергию беспорядочного теплового движения, осуществляя тем самым процесс теплопроводности, в котором колебания узлов (ионов) решетки принимают незначительное участие при низких и комнатных температурах. С ростом температуры влияние последних усиливается, создавая помехи движению электронного газа, так что чем выше температура чистого метала, тем хуже он проводит тепло. Опыты свидетельствуют, что для сплавов не имеется однозначной связи между ростом их температуры и падением проводимости тепла.

В диэлектриках нет свободных электронов и перенос тепла в них осуществляется за счет колебания узлов решеток (фононная проводимость тепла). Если в каком-то месте диэлектрик нагревают, то усиливающиеся в нем колебания узлов распространяются в теле в виде затухающей волны, так как узлы связаны межмолекулярным взаимодействием.

В полупроводниках, находящихся при низких температурах, мало свободных электронов и тепло в них при этом распространяется, как в диэлектрике. При средних температурах вклад электронной проводимости возрастает, а при высоких температурах она становится преобладающей.

В неподвижных газовых слоях носителями тепла являются хаотически движущиеся молекулы (атомы). Если газ в каком-то месте нагревать, то в нем увеличивается среднеквадратичная скорость движения молекул, которые, сталкиваясь с более удаленными медленными (холодными) молекулами, увеличивают их кинетическую энергию и, как следствие, при этом увеличивается и температура газа.

Наименее изучен процесс теплопроводности в жидкостях. Не вдаваясь в детали теории жидкого состояния вещества, укажем на то, что в настоящее время полагают, что жидкости в течение некоторого очень малого промежутка времени, называемого временем релаксации, можно рассматривать как кристаллические структуры. Затем эти структуры разрушаются и поведение жидкости соответствует газовому состоянию. В каждом из этих чередующихся состояний действует свой механизм переноса тепла.

1.2. Основные понятия теплопроводности (и теплопередачи)

К ним относятся следующие понятия: температура, температурное поле, изотермическая поверхность, изотерма, градиент температуры, тепловой поток, плотность теплового потока.

Температура – это физическая величина, являющаяся мерой отклонения состояния тела от теплового равновесия с другим телом, называемым эталоном, температуру которого условно принимают равной нулю. В зависимости от выбора тела-эталона различают эмпирические и абсолютные шкалы температур.

В России принята эмпирическая стоградусная шкала Цельсия, в которой тепловое состояние тел сравнивают с тепловым состоянием тающего при нормальном давлении химически чистого водного льда: темпера­туру последнего полагают равной 0^С. Нужно иметь в виду, что в большинстве англоязычных стран мира принята шкала Фаренгейта, и обращать внимание на то, в какой шкале измерения сообщается температура.

В абсолютной шкале температур (в термодинамической шкале температур, в шкале Кельвина) тепловое состояние тела сравнивают с таким его же состоянием, при котором достигается минимальное значение внутренней энергии: температуру последнего состояния полагают равной 0 К.

Связь между значением температуры Т в абсолютной шкале и значением температуры t в шкале Цельсия дается соотношением

T = t+273,15.

Основной задачей теории теплопроводности является определение температуры Т в любой точке M   ( – геометрическая область, занимаемая телом) в любой момент времени  > 0 , отсчитываемый от начала нагревания или охлаждения тела. Совокупность значений Т(М, ) в фиксированный момент времени  называется температурным полем в теле. Можно, таким образом, сказать, что основной задачей теории теплопроводности является определение температурного поля в теле в каждый момент времени .

Естественно, что температурное поле можно представить в виде совокупности («набора») так называемых изотермических поверхностей. Изотермическая поверхность – это реальная или воображаемая геометрическая поверхность, в каждой точке которой в данный момент времени температура одинакова. Из физических соображений ясно, что изотермические поверхности не могут пересекаться друг с другом, они замыкаются сами на себя или на ограничивающие тело поверхности.

Пересечение изотермических поверхностей плоскостями дает линии–изотермы.

В теории теплопроводности аналитическими методами чаще всего рассматривается распространение тепла в телах простейшей формы – в неограниченной пластине и в сплошных или полых шаре и круговом цилиндре неограниченной или конечной длины. Отметим, что под неограниченной пластиной понимается параллелепипед, у которого две протяженности во много раз больше третьей, называемой толщиной пластины .

На рис. 1.1 изображены в виде примера изотермические поверхности (рис. 1.1, а) и изотермы (рис. 1.1, б) в неограниченной пластине, в круговом цилиндре неограниченной длины и сплошном шаре в какой-то момент времени при условии, что их ограничивающие поверхности в процессах нагревания или охлаждения поддерживаются изотермическими.

Рис. 1.1

Отметим, что сечения изотермических поверхностей получены плоскостями, перпендикулярными ограничивающим поверхностям пластины, оси цилиндра или проходящими через центр шара.

Рассмотрим в виде примера нагревание прямолинейного бруса (призмы) неограниченной длины с произвольным по форме поперечным сечением, наружная поверхность которого поддерживается изотермической. Выделим в поперечном сечении, перпендикулярном оси бруса, изотермы Т – Т, Т и Т + Т (рис. 1.2). Затем на изотермической поверхности с температурой Т рассмотрим ее элемент с единичной площадью. Тепло с этой площадки будет передаваться в направлении изотермической поверхности с температурой Т – Т (Т – Т < Т < Т + Т), очевидно, под действием движущей силы в виде разности температур T – (Т – Т) = Т.

Предел отношения Т к расстоянию n, взятому по нормали к рассматриваемым изотермическим поверхностям, т.е. величина

называется градиентом температуры в указанном месте на изотермической поверхности с температурой Т. Величина gradT является вектором, направленным в сторону больших значений температур в теле.

Именно градиент температуры gradT выступает в качестве движущей силы процесса теплопроводности.

Рис. 1.2

Количество тепла, проходящего через всю площадь изотермической поверхности за время , называется тепловым потоком Q [Дж], а та его часть, которая проходит через единицу площади за единицу времени, называется плотностью теплового потока [Вт/м²]. 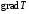Плотность теплового потока является вектором, направленным в сторону меньших значений температуры, и для изотропных тел он находится на одной прямой с градиентом температуры , т.е. угол между этими векторами равен .