1.5. Краевые условия для уравнения Фурье

Уравнение Фурье представляет собой дифференциальное уравнение в частных производных второго порядка и его решение (интегрирование) приводит к появлению в структуре решения произвольных функций от аргументов x, y, z, , т.е. получаем при этом неоднозначное решение о температурном поле в теле.

Чтобы эти произвольные функции определить и получить однозначное решение поставленной задачи, очевидно, что к уравнению Фурье должны быть присоединены дополнительные уравнения, представляющие собой математическое описание известных условий протекания исследуемого процесса теплопроводности. Эти условия называются краевыми, так как они содержат в себе информацию об условиях на «краях» рассматриваемого явления.

Процесс нестационарной теплопроводности развивается во времени и в пространстве и имеет на них края.

Временным краем процесса является момент его начала, соответствующий моменту времени  = 0, отсчитываемому от начала нагревания или охлаждения тела. Температурное поле в теле при  = 0 полагают известным и представляют в виде зависимости

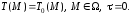(1.19)

Формула (1.19) является математической записью начального условия задачи нестационарной теплопроводности. При одинаковой начальной температуре во всех точках тела это условие становится простейшим и принимает вид

(1.19)

В пространственные края включаются все точки на всех ограничивающих тело поверхностях. На пространственных краях полагают известными тепловые условия в течение всего процесса теплопроводности и их математическую запись называют граничными условиями для уравнения Фурье.

Рассматриваемое твердое тело может омываться потоками жидкости (газа), нагреваться (или остывать) излучением, на его поверхностях могут быть размещены нагреватели и т.п. В зависимости от рода известной информации о тепловой обстановке на ограничивающих поверхностях тела различают граничные условия первого (ГУ-I), второго (ГУ-II), третьего (ГУ-III) и четвертого (ГУ-IV) рода.

Если из физических соображений или в результате проведенных измерений известна температура T_W на поверхности Г тела, то мы располагаем граничными условиями первого рода в форме

(1.20)

В простейшем случае в течение всего процесса во всех точках на всех поверхностях тела температура одинакова, и тогда вместо (1.20) имеем ГУ-I в виде

(1.20)

Если известна плотность теплового потока q на поверхности тела, то к уравнению Фурье присоединяют ГУ-II в форме

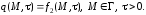(1.21)

С учетом (1.4) формула (1.21) принимает вид

(1.21)

или

(1.21)

Граничные условия третьего рода (ГУ-III) присоединяют к уравнению Фурье в том частном случае, когда тело омывается потоком жидкости (газа), температура которого на удалении от тела известна (рис.1.6).

Рис. 1.6

При этом плотность теплового потока, передаваемого от движущейся среды к поверхности тела, полагают пропорциональной разности температур T_W – (температура поверхности T_W неизвестна и сама подлежит определению)

(1.22)

Чтобы перейти в (1.22) от пропорции к равенству, вводится коэффициент пропорциональности , называемый коэффициентом теплоотдачи, так что имеем

(1.22)

В формуле (1.22) считаются известными лишь величины и . Величина  численно равна плотности теплового потока, передаваемого от поверхности тела при = 1K:

(1.23)

Зависит величина  от следующих факторов:

1. от относительной скорости потока (чем эта скорость больше, тем больше и );

2. от режима его течения у поверхности тела (в дальнейшем будут рассмотрены ламинарный, переходной и турбулентный режимы течения);

3. от теплофизических свойств движущейся среды (например, для жидкостей  больше, чем для газов);

4. от формы обтекаемого тела (у плохо обтекаемых тел в потоке образуются вихри, он турбулизируется, и вследствие этого  становится больше);

5. от шероховатости поверхности (для большей шероховатости  больше вследствие упомянутой выше турбулизации течения).

Плотность теплового потока, передаваемого через ограничивающую поверхность тела, «входит» внутрь твердого тела (или «выходит») механизмом теплопроводности и для ее определения применима также формула (1.4), так что вместо (1.22) имеем также

(1.24)

или

(1.24)

Граничные условия четвертого рода относятся к специфическому случаю теплового контакта между двумя твердыми телами (рис. 1.7). При этом возможен случай идеального теплового контакта (вариант а, когда поверхность Г тел № 1 и № 2 является общей) и неидеального теплового контакта (вариант б на рис. 1.7), когда поверхности Г тел № 1 и № 2 разделены газовой прослойкой, слоем окислов, слоем масла и т.п.

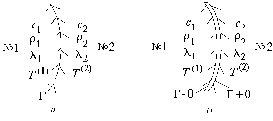
Рис. 1.7

Ясно, что в обоих случаях плотности теплового потока, пересекающего поверхность Г слева (Г–0) направо (Г+0), совпадают, так что с привлечением (1.4) имеем

(1.25)

В случае идеального теплового контакта на поверхностях Г–0 и Г+0 в течение всего процесса совпадают и температуры контактирующих тел:

(1.26)

а в случае неидеального теплового контакта имеет место скачок температуры T, формирующийся на термическом сопротивлении, разделяющем оба тела, т.е. выполняется равенство

(1.27)