2.5. Критериальные формулы для описания теплообмена во внешней задаче (вынужденное течение)
Во внешней задаче по мере удаления потока от передней кромки пластины формируются динамический и тепловой пограничные слои, профили скорости и температуры при этом перестраиваются. Вследствие этого существенными для развития процесса являются мера отношения силы инерции к силе вязкостного трения, т.е. критерий Рейнольдса, и мера отношения конвективного потока тепла к потоку тепла, переносимого теплопроводностью, т.е. критерий Пекле. Поэтому критериальная зависимость для описания конвективного теплообмена в рассматриваемой ситуации должна иметь вид
.
На участке ламинарного пограничного слоя 0 < x < xкр (рис. 2.6) критериальная формула для расчета среднего числа Нуссельта такова:
(2.35)
Если длина участка ламинарного течения мала, то полагают, что вся пластина омывается течением с турбулентным пограничным слоем. Для этого случая критериальная формула для расчета среднего значения числа Нуссельта установлена в следующем виде:
(2.36)
В
формулах (2.35), (2.36)
и
– средние значения числа Нуссельта и
коэффициента теплоотдачи на участке
пластины длиной x,
отсчитанной от передней кромки; Re
= wx/
– критерий Рейнольдса;
– температурный фактор.
Отметим
сразу, что величина
учитывает влияние направления теплового
потока (в стенку или от стенки) на
интенсивность конвективного теплообмена.
Учет ее влияния будет предметом отдельного
рассмотрения.
Для
описания конвективного теплообмена на
пластине с учетом конечной протяженности
участка ламинарного пограничного слоя
установлена следующая зависимость для
расчета среднего значения коэффициента
теплоотдачи на участке турбулентного
течения (
):
,
(2.37)
в
которой
определяется согласно (2.35), а
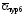рассчитывается по формуле
,
(2.38)
где
,
,
.
Величина
равна длине участка такой пластины, от
переднего края которой сформировался
бы турбулентный пограничный слой той
же толщины, которую имеет ламинарный
пограничный слой на расстоянии
на реальной пластине длиной x.
В
приведенных формулах теплофизические
характеристики среды
,
и Pr
выбираются из таблиц по температуре
набегающего потока
.
Хотелось бы обратить внимание на важность достоверного определения точки перехода ламинарного пограничного слоя в турбулентный, так как в этом месте скачком возрастает коэффициент теплоотдачи , и если пластина омывается высокотемпературным потоком газа, то скачком возрастает и температура поверхности. С ростом температуры материала уменьшаются все известные пределы прочности (на разрыв, на кручение и т.д.), и если конструкция «нагружена» в силовом отношении, то в точке x=xкр она может начать разрушаться.
Рис. 2.10
Особенно актуальна эта задача для рабочих лопаток высокотемпературных турбин авиационных двигателей, на спинке (точка а) и на корытце (точка б) которых наблюдается явление перехода течения в пограничном слое из ламинарного в турбулентное (рис. 2.10).
2.6. Критериальные формулы для описания теплообмена во внутренней задаче (вынужденное течение)
Теплообмен в канале определяется, как это было показано в 2.3, режимом течения и теплофизическими характеристиками движущейся среды, но независимо от них распределение интенсивности теплообмена по длине трубы имеет в соответствии с изложенным в 2.4 вид, приведенный на рис. 2.11.
Рис. 2.11
Отметим сразу, что рассматривается теплообмен в канале, на входе которого профиль скоростей уже стабилизировался, т.е. предполагается наличие предвключенного гидродинамического участка, на котором теплообмен отсутствует.
Вследствие этого при ламинарном режиме течения сила инерции становится пренебрежимо малой по сравнению с силой вязкостного трения, а мера их отношения – критерий Рейнольдса – вырождается и выпадает из числа аргументов для описания интенсивности теплообмена.
При турбулентном режиме течения даже при стабилизировавшемся профиле скорости вследствие турбулентных пульсаций в потоке существенными являются и инерционные силы и силы вязкостного трения, так что мера их отношения – критерий Re – должна быть включена в качестве аргумента для числа Nu. Турбулентные же пульсации температуры на участке стабилизировавшейся теплоотдачи приводят к тому, что существенным для интенсивности теплопереноса в потоке остается и критерий Pe.