14. Сеточный метод решения одно- и двумерных задач нестационарной теплопроводности

Метод сеток практически совпадает с методом элементарного теплового баланса. Отличие между ними состоит в том, что, во-первых, метод сеток обосновывается формальной дискретизацией уравнений исходной краевой задачи нестационарной теплопроводности и, во-вторых, полученный таким образом разностный аналог уравнения нестационарной теплопроводности относят ко всем элементарным слоям, на которые мысленно разбивается исходная геометрическая область протекания процесса, т.е. не рассматривают отдельно, как в методе элементарного теплового баланса, пристенные слои.

Исходное нелинейное уравнение нестационарной теплопроводности, имеющее для неограниченной пластины в одномерной постановке вид

, (1.68)

при использовании неявной безытерационной схемы дискретизируется относительно середины i-го слоя (рис. 1.11) следующим образом:

, (1.69)

Приравнивая правые части формул (1.69) , (1.70), получаем разностный аналог уравнения (1.68) в виде

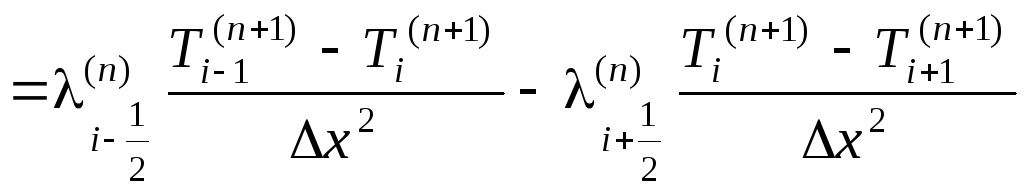, (1.71)

где .

Для того чтобы уравнение (1.71) было отнесено ко всем элементарным слоям неограниченной пластины, включая первый и последний слои, ее ограничивающие плоскости в отличие от рассмотренного в п. 1.8.1 метода элементарных тепловых балансов мысленно «наращивают» двумя фиктивными слоями (рис. 1.11).

Для решения системы уравнений (1.71) ее нужно замкнуть путем присоединения двух дополнительных уравнений, представляющих собой конечно-разностный аналог граничных условий. При их формулировке полагают, что между серединами первого фиктивного слоя и примыкающего к нему первого (по оси Ох) слоя пластины и между серединами последнего слоя пластины и примыкающего к нему второго фиктивного слоя температуры распределены в пространстве линейно, т.е. выполняются равенства , (1.72) . (1.73)

Рис. 1.11

С учетом (1.72), (1.73) граничные условия третьего рода (1.66), (1.67) записываются как

, (1.74)

. (1.75)

Решая совместно систему уравнение (1.71), (1.74), (1.75) на каждом временном слое длительностью относительно массива , находим температуры в серединах двух фиктивных слоев и в серединах m реальных слоев, что позволит найти согласно (1.72), (1.73) и температуры ограничивающих поверхностей и .

Формулы (1.72) и (1.73) представляют собой задание граничных условий первого рода в том случае, если температуры и не подлежат определению, а заданы. Если же заданы граничные условия второго рода (плотности тепловых потоков и на ограничивающих поверхностях пластины), то с учетом (1.72), (1.73) они будут представлены в виде

, (1.76)

. (1.77)

Если направления векторов и совпадают с направлением оси Ox, то в (1.76), (1.77) их численные значения положительны.

Метод сеток позволяет решать и многомерные нелинейные задачи нестационарной теплопроводности. В этом случае на тело наносится сетка, т.е. его, например при рассмотрении двухмерного температурного поля, мысленно делят на элементарные прямоугольники со сторонами и , которые представляют собой шаги по пространственным переменным x и y, при выборе в качестве шага по времени. Нетрудно видеть (рис. 1.12), что линия, ограничивающая плоскую область, в этом случае заменяется на ломаную, состоящую из участков, параллельных осям 0x и 0y.

Можно показать, что в этом случае исходное нелинейное уравнение нестационарной теплопроводности вида

(1.78)

при использовании безытерационной неявной схемы имеет следующий конечно-разностный аналог:

, (1.79)

.

Рис. 1.12

Для того чтобы уравнение (1.79) было отнесено ко всем элементарным прямоугольникам, включая все приповерхностные слои тела, его сеточный аналог, ограниченный ломаной линией (изображена на рис. 1.12 в виде жирной линии), должен быть мысленно «наращен» фиктивными прямоугольными элементами (изображены на рис. 1.12 примыкающими вне границы сеточного аналога). Тогда числа M и N в формуле (1.79) представляют собой максимальное количество элементарных прямоугольников (в том числе и фиктивных) по направлениям осей 0x и 0y соответственно.

Для решения системы уравнений (1.79) ее нужно замкнуть путем присоединения дополнительных уравнений, представляющих собой конечно-разностный аналог граничных условий. При их формулировке полагают, как и в одномерной задаче, что между серединами фиктивных и примыкающих к ним прямоугольников температуры распределены в пространстве линейно. Решение построенной таким образом системы уравнений позволяет находить неизвестные температуры в центрах выделенных прямоугольников на каждом временном слое.

Экономичные схемы проведения расчетов на ЭВМ предполагают применение дробных шагов по времени (обосновано акад. Н.Н. Яненко) или расщепление исходной задачи (1.78) на серию локально-одномерных задач по направлениям координатных осей (обосновано акад. А.А.Самарским).

Применительно к рассматриваемой нами задаче вместо конечно-разностных уравнений (1.51) по методу А.А. Самарского на временном слое длительностью сначала решают серию из (N–2) задач по направлению оси 0x

и затем, используя полученные значения , решают серию из (M–2) задач по направлению 0y:

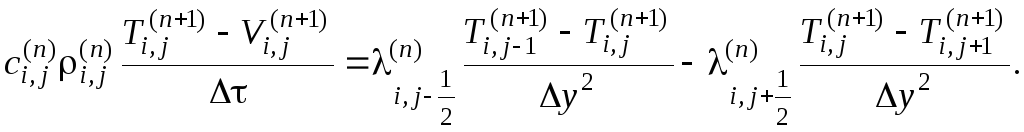
Необходимо отметить, что разности температур в разных точках тела в одинаковые моменты времени (в правых частях формул (1.63), (1.64), (1.65), (1.71), (1.79) и т.д.; в обеих частях (1.66), (1.67), (1.74), (1.75); в левых частях (1.76), (1.77)) построены таким образом, что температуры в них последовательно записываются в порядке их расположения по соответствующим координатным осям. Таким приемом удается простейшим способом сохранить одинаковые знаки левых и правых частей перечисленных выше формул.