11. Два метода расчета та.

Тепловой расчет ТА может быть проектным (конструкторским) и поверочным. Задача проектного расчета - определение величины и формы поверхности теплообмена, разделяющей горячую и холодную среды. Поверочный расчет выполняется в том случае, когда величина и форма поверхности задана, т.е. известна конструкция ТА. Задача поверочного расчета – определение количества передаваемой теплоты и конечных температур рабочих сред. Указанные задачи решаются двумя методами:

1 Метод среднего логарифмического температурного напора

2 Метод эффективности теплообменника по числу единиц переноса теплоты

Принципиально методы базируются на уравнении теплового баланса и уравнении теплопередачи. Отличие лишь в выборе параметров.

Уравнение теплопередачи: , -коэфф.теплопередачи.

Уравнение теплового баланса:

–водяные эквиваленты.

плюс - для прямотока; минус – для противотока.

Зависимость темпер-ры теплоносителей от теплоемкости массовых расходов для прямоточной (а) и противоточной схемы (б) (W-это С)

Из уравнения (*) видно, что отношение температурных напоров выходного к входному зависит от двух важных безразмерных параметров:

- число единиц переноса теплоты

Тепловая эффективность (КПД) теплообменника определяется отношением теплопроизводительности аппарата к ее предельному значению :

;

Если :

Если :

Обычно в теплообменниках

Для прямоточной схемы :

Для противоточной схемы:

зависит от и

При расчете методом средних логарифмических температурных напоров применяется уравнение:

–поправка к среднелогарифмическому напору.

Если теплообменник противоточный, то Для всех остальных схем и он определяется схемой движения и двумя безразмерными параметрами Р и R.

Если , то . Если , то

Из уравнения теплового баланса для всего теплообменника: ; .

Анализ методов и среднелогарифмического температурного напора показали, что они дают одинаковые расчеты, но метод менее трудоемок из-за отсутствия в нем последовательных приближений.

12. Конструкции и расчет тепломассообмена выпарных аппаратов с естественной циркуляцией.

13. Порядок расчета подогревателя воды выхлопными газами ГТД.

Исходные данные:

– расход газа в межтрубном пространстве; - температура газа на входе в теплообменник; - температура газа на выходе из теплообменника; – давление газа на входе в теплообменник; – давление газа на выходе из теплообменника; давление воды на входе в теплообменник; температура воды на входе в теплообменник; температура воды на выходе из теплообменника; скорость воды в трубках; наружный диаметр трубок; толщина стенки трубки; толщина ребра на трубке; зазор между ребрами на трубке; шаг оребрения; коэффициент теплопроводности материала трубки и ребер (из Я1Т).

Порядок расчета:

1 Задаемся диагональным шагом:

2 Параметр для определения поперечного шага трубок и продольного :

3 Поперечный и продольный шаг трубок:

4 Высота ребра по ходу газа продольная и поперечная: ;

5 Коэффициент загромождения фронта теплообменника трубками и оребрениями:

6 Расчет передаваемой теплоты:

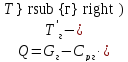
7 Потребный расход воды:

8 Температурный напор на входе и на выходе газа:

9 Среднелогарифмический температурный напор для противотока:

10 Поправочный коэффициент:

11 Среднелогарифм. Темпер. напор для противоточной схемы:

12 Число Рейнольдса в трубках:

13 Число Нуссельта в трубках:

14 Коэффициент теплоотдачи в трубках:

15 Общая длина трубок определяется по теплоте:

16 Потребная площадь внутри трубок и потреб. Их длина :

17 Число трубок на вход воды:

18Длина одной трубки от входа к выходу на n ходов:

19 Высота теплооб-ка при n пучках: 20 Число трубок на один раз:

21 Ширина теплообменника по фронту: 22 Площадь фронта:

23 Площадь проходных ячеек во фронте:

24 Скорость в ячейках межтрубного пространства:

25 Коэффициент теплоотдачи в ячейках межтрубного пространства:

26 Коэффициент оребрения:

27 Теплоотдача на оребрении при ламинарном течении:

28 Теплоотдача при турбулентном течении:

,

29 Расчет эффективности ребра: Параметр m для ребра:

30 Эффективный коэфф-т теплоотдачи в межтрубном пространстве:

31 Коэффициент теплопередачи от газа к воде:

32 Мощность теплообменника:

14. Конструкции и расчет тепломассообмена выпарных аппаратов с принудительной циркуляцией.

15. Расчет эффективности ребра.

Для удобства расчета теплоотдачи оребренной поверхностью вводят коэффициент эффективности ребра Е, иногда называемый коэффициентом полезного действия ребра. Согласно определению, коэффициент эффективности ребра - это отношение количества тепла, переданного ребристой поверхностью, к тому количеству тепла, которое могло бы быть передано в случае бесконечной теплопроводности ребер.

_{Рассмотрим способ определения величины} Е для ребер различной конфигурации. Одномерное дифференциальное уравнение теплопроводности для ребра постоянного попе-речного сечения имеет вид где х - продольная координата ребра, отсчитываемая от его основания; θ = t - t₁ - местная избыточная температура ребра; t и t₁ - местная температура ребра и постоянная температура омывающего его газа; и и f_p - периметр и площадь поперечного сечения ребра; λ_p и α_р - коэффициент теплопроводности и средний коэффициент теплоотдачи на его боковых поверхностях. Решая дифференциальное уравнение теплопроводности при заданной температуре t₀ в основании ребра (х = 0) и отсутствии теплообмена через торец ребра, получим где h_р - высота ребра; θ₀ = t₀ - t₁

Теплота, передаваемая через ребро, находится из соотношения С другой стороны, величина Q_p может быть определена из закона Ньютона – Рихмана где F_p - поверхность ребра. Приняв α_р = const, получим среднеинтегральная избыточная температура поверхности ребра. При бесконечно большой теплопроводности ребра температура его поверхности будет приближаться к температуре в основании, и отдаваемое количество теплоты составит Тогда согласно данному выше определению коэффициент эффективности ребра (*)Из уравнения (*) видно, что в качестве коэффициента эффективности ребра можно принимать отношение средней разности температур оребренной поверхности и окружающей среды к разности температур поверхности, несущей оребрение, и окружающей среды. Для ребра постоянного поперечного сечения коэффициент эффективности В случае тонких призматических ребер с периметром u = 2b + 2δ_р ≅ 2b (здесь b - ширина, δ_р - толщина ребра) параметр Тогда, если воспользоваться числом Био Bi = (δ_р/λ_р):(1/α_р), которое представляет собой отношение внутреннего термического со-противления теплопроводности к внешнему термическому сопротивлению теплоотдаче, то и коэффициент эффективности призматического ребра (**) Формула (**) справедлива для прямых ребер постоянного поперечного сечения, рас-положенных на плоской стенке. Если ребро имеет форму диска на цилиндрическом основании, то при постоянной толщине ребра решение принципиально не отличается от изложенного выше. В этом случае дифференциальное уравнение одномерной теплопроводности есть уравнение Бесселя, имеющее решение в цилиндрических (бесселевых) функциях .

Для широко используемых круглых дисковых ребер переменной толщины - радиальная продольная координата ребра) уравнение теплопроводности примет вид :

Где θ = t - t₁ - местная избыточная температура ребра; t и t₁ - местная температура ребра и постоянная температура омывающего его газа,- периметр поперечного сечения ребра; λ_p и α_р - коэффициент теплопроводности и средний коэффициент теплоотдачи на его боковых поверхностях. Уравнение (1) может быть проинтегрировано для целых и дробно-рациональных, функций δ_р(r). Его общее решение выражается через бесселевы функции 1-гo и 2-го рода n-го порядка. Например, в простейшем случае для радиального ребра постоянной толщины где J₀(mr) и К₀(mr) - модифицированные функции Бесселя 1-го и 2-го рода нулевого порядка. Определить значения функции Бесселя для конкретной величины аргумента mr можно с помощью таблиц или путем вычисления на ЭВМ по стандартным программам. Постоянные С₁ и C₂ находятся из граничных условий в основании и на торце ребра.

Рис. 12. К определению коэффициента эффективности круглых ребер постоянного сечения (а) и поправочного коэффициента для трапециевидных ребер (б)

Аналитическое выражение коэффициента тепловой эффективности дискового ребра даже постоянной толщины имеет сложный вид, и расчет величины Е достаточно трудоемок. Поэтому при проектировании теплообменных аппаратов используется ее графическая интерпретация (рис. 12,а), где Е рассчитано по указанной аналитической зависимости. На графике в качестве аргумента использована величина

, (58)

где, согласно сделанному ранее замечанию об учете теплоотдачи с торца, h = h_p + δ_р/2.

16. Пленочные выпарные аппараты и расчет тепломассообмена в них.

17. Расчет гидросопротивлений в пучке оребренных труб.

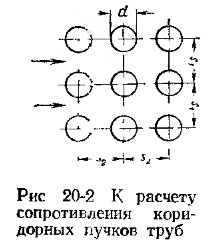Определение гидросопротивлений:

S₁-поперечный шаг,S-диагональный шаг,z-число рядов по ходу газа

18. Схемы и расчет многокорпусных выпарных аппаратов.

19. Сопоставление методов и среднелогарифмического температурного напора по порядку расчета параметров (по разделу 1).

1) Дано: коэффициент теплопередачи k, водяные эквиваленты C₁,C₂,t׳₁, t׳׳₁, t׳₂,t׳׳₂.

Найти: поверхность теплообмена F.

Метод Ntu	средне логарифмический напор
	По схеме, R,P определяем
По схеме ε,CR определяем Ntu	Определяем

Оба метода дают прямое решение, так как заданы конечные температуры теплоносителей.

2) Дано:F, k, C₁, C₂, t׳₁, t׳₂

Найти: t׳׳₁,t׳׳₂,

Метод Ntu	средне логарифмический напор
	Задаем t2׳׳ и определяем Р
	По R,P, виду схемы определяем
Находим ,	Определяем (для противотока)
	По находим Проверяем. Если не совпадает, то повторяем расчет.

20. Основные сведения по адсорбции жидкостей и газов.

21. Сопоставление методов и среднелогарифмического температурного напора по порядку расчета параметров (по разделу 2).

1) Дано: коэффициент теплопередачи k, водяные эквиваленты C₁,C₂,t׳₁, t׳׳₁, t׳₂,t׳׳₂.

Найти: поверхность теплообмена F.

Метод Ntu	средне логарифмический напор
	По схеме, R,P определяем
По схеме ε,CR определяем Ntu	Определяем

Оба метода дают прямое решение, так как заданны конечные температуры теплоносителей.

22. Материальный и тепловой баланс процесса адсорбции.

23. Понятия коэффициента сопротивления для каналов.

Потери давления потока разделяют на два вида: потери на трение Δр_тр и потери на преодоление местных сопротивлений Δр_м. Потери на трение играют главную роль при упорядоченном движении среды вдоль твердой поверхности, например в каналах, и обусловлены молекулярным и турбулентным обменом количествами движения между слоями жидкости или газа. Местные потери возникают при нарушении упорядоченного течения, отрыве потока от стенок, вихреобразовании и интенсивном турбулентном перемешивании в местах резкого изменения границ течения. Эти явления усиливают обмен количеством движения между частицами движущейся среды, интенсифицируя процесс диссипации механической энергии.

При определении гидравлического сопротивления канала, в котором присутствуют оба вида потерь, они суммируются: Δр = Δр_м. + Δр_тр . (1)

Такой же подход используют и при расчете любого тракта, составленного из различных участков течения:

В расчетах потерь давления оперируют безразмерными коэффициентами сопротивления, которые представляют собой отношение потерянной мощности ΔN на данном участке потока к кинетической энергии в единицу времени в некотором сечении потока F: (3) , где G - массовый расход среды; с - среднерасходная скорость.

При постоянной плотности среды ρ выражение (3) преобразуется к виду (4)

В соответствии с формулой (1) при неизменной скорости потока коэффициент сопротивления ζ =ζ_м + ζ_тр . (5)

Здесь ζ_м = Δр_м/(ρс²/2) - коэффициент местного сопротивления, а ζ_тр = Δр_тр/(ρс²/2) - коэффициент сопротивления трения. Коэффициент сопротивления трения согласно формуле Дарси выражается через коэффициент потерь на трение λ_тр следующим образом:

ζ_тр = λ_тр L/d_г , (6) где λ_тр - относительные потери давления на трение, приходящиеся на длину одного калибра канала; L/d_г - число калибров; L - длина канала; d_г - его гидравлический диаметр. При этом формула (5) запишется в виде ζ =ζ_м + λ_тр L/d_г . (7)

В сложном тракте, на различных участках которого скорость потока меняется, общие потери давления определяются согласно формуле (2). Подставив в нее коэффициенты сопротивлений, получим (8) , где ζ_мj и λ_j — коэффициенты местных сопротивлений и потерь трения для различных участков тракта теплоносителя. Каждый из трактов характеризуется своей величиной общих потерь давления: для воздушного тракта Δр₁, для водяного Δр₂.

24. Устройство адсорберов и процессы тепломассообмена с неподвижным и движущимся зернистым адсорбентом.

25. Конструкции и процессы тепломассообмена псевдожидкостного слоя мелкозернистого адсорбента.

26. Основные сведения по процессу экстракции компонентов из твердых веществ.

27. Устройства и расчет тепломассообмена экстракторов насадочного типа.

28. Устройства и расчет тепломассообмена экстракторов ректификационного типа.

29. Основные сведения по процессу сушки.

30. Устройства и расчет тепломассообмена конвективных сушилок.

31. Отличие процессов тепломассообмена в теоретической конвективной сушилке от процессов в реальной конвективной сушилке.

32. Устройства и расчет тепломассообмена контактных сушилок прямого и непрямого действия.

33. Специальные методы сушки токами высокой частоты и сублимацией.

34. Равновесие в системах жидкости газа. Законы Генри и Рауля.

35. Основные сведения о закономерностях процессов абсорбции.

36. Материальный и тепловой баланс процесса абсорбции.

37. Конструкции и тепломассообмен абсорберов поверхностного типа.

38. Конструкции и тепломассообмен барботажных абсорберов.

39. Конструкции и тепломассообмен распыливающих абсорберов.