
- •Электростатика и постоянный ток
- •Электрический заряд и его свойства. Закон Кулона.
- •Электрическое поле. Напряженность электростатического поля.
- •Потенциальная энергия взаимодействия. Работа электростатического поля. Потенциал.
- •Связь напряженности электростатического поля и потенциала.
- •Потенциальные диаграммы. Поле заряженной плоскости.
- •Поток вектора напряженности. Теорема Гаусса.
- •Дивергенция вектора напряженности. Истоки и стоки электрического поля.
- •Электрический диполь. Диполь в однородном и неоднородном электрическом поле.
- •Циркуляция вектора напряженности электростатического поля. Интегральное условие потенциальности электростатического поля.
- •Ротор вектора. Дифференциальное условие потенциальности электрического поля.
- •Электроемкость уединенного проводника.
- •Конденсаторы. Плоский и цилиндрический конденсаторы.
- •Диэлектрики. Типы диэлектриков.
- •Поляризация диэлектриков. Вектор поляризации.
- •Свободные и связанные заряды. Диэлектрическая проницаемость среды.
- •Вектор электрического смещения. Теорема Гаусса для поля в веществе.
- •Граничные условия, преломлений линий е и d.
- •Энергия плоского конденсатора. Объемная плотность энергии электростатического поля.
- •Электрический ток. Условие существования тока. Плотность тока. Уравнение непрерывности.
- •Закон Ома для участка цепи и цепи, содержащей эдс. Закон Ома в дифференциальной форме.
- •Закон Джоуля Ленца в интегральной и дифференциальной формах.
- •Сторонние силы. Э.Д.С. Источника тока. Основные закономерности электрических цепей. Правила Кирхгофа.
- •Электрический ток в газах. Процессы ионизации и рекомбинации.
- •Электрический ток в вакууме. Термоэлектронная эмиссия.
- •Электромагнетизм
- •Сила Лоренца. Движение заряженных частиц в электромагнитном поле.
- •Сила Ампера. Рамка с током в магнитном поле. Закон Ампера.
- •Принцип суперпозиции магнитного поля. Закон Био-Савара-Лапласа.
- •Циркуляция вектора магнитной индукции. Закон полного тока.
- •Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.
- •Работа магнитного поля.
- •Магнитное поле в веществе. Намагниченность.
- •Напряженность магнитного поля. Закон полного тока.
- •Магнетики: диа-, пара-, и ферромагнетики.
- •Электромагнитная индукция. Закон Фарадея для электромагнитной индукции. Правило Ленца.
- •Потокосцепление, самоиндукция. Индуктивность.
- •Токи замыкания и размыкания цепи. Токи Фуко.
- •Система уравнений Максвелла в интегральной и дифференциальной формах.
- •Колебания и волны
- •Характеристики колебательных процессов. Гармонические колебания. Частота и фаза колебаний.
- •Векторная диаграмма гармонических колебаний.
- •Сложение колебаний одинакового направления и одинаковой частоты.
- •Сложение взаимноперпендикулярных колебаний. Фигуры Лиссажу.
- •Гармонические осцилляторы. Пружинный маятник.
- •Колебательный контур.
- •Одномерное волновое уравнение. Групповая скорость, связь ее с фазовой скорость. Дисперсия.
- •Интерференционные полосы равной толщины. Кольца Ньютона.
- •Дифракция волн. Принцип Гюйгенса-Френеля. Метод зон Френеля.
- •Простые задачи дифракции: дифракция на круглом отверстии, на круглом препятствии (по Френелю).
- •Интерферометры. Понятие о голографии.
- •Дифракция на одной щели.
- •Естественный и поляризованный свет. Поляризация света. Закон Малюса.
- •Поляризация при отражении и преломлении на границе диэлектрика. Закон Брюстера.
Энергия плоского конденсатора. Объемная плотность энергии электростатического поля.
Энергия плоского
конденсатора:
 .
.
Если учесть что
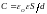 ,
то получим
,
то получим
 (1) где
(1) где
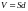 - объём, в котором сосредоточено
электрическое поле плоского конденсатора.
- объём, в котором сосредоточено
электрическое поле плоского конденсатора.
Следовательно,
электрическая энергия конденсатора
может быть выражена двумя различными
способами. Во-первых, она может быть
выражена через заряды на обкладках
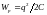 .
При таком подходе эта энергия выступает
как энергия зарядов и поэтому её
носителями являются электрические
заряды. Во-вторых, эта же энергия может
быть выражена через напряженность
электрического поля между обкладками
(1). При таком подходе в роли носителя
электрической энергии выступает поле,
по объёму которого и распределена вся
энергия. Такая точка зрения называется
полевой
концепцией электрической энергии. В
рамках этой концепции первый множитель
в (1) имеет смысл энергии, заключенной в
единице объема однородного поля и
называется объемной
плотностью энергии электрического
поля.
.
При таком подходе эта энергия выступает
как энергия зарядов и поэтому её
носителями являются электрические
заряды. Во-вторых, эта же энергия может
быть выражена через напряженность
электрического поля между обкладками
(1). При таком подходе в роли носителя
электрической энергии выступает поле,
по объёму которого и распределена вся
энергия. Такая точка зрения называется
полевой
концепцией электрической энергии. В
рамках этой концепции первый множитель
в (1) имеет смысл энергии, заключенной в
единице объема однородного поля и
называется объемной
плотностью энергии электрического
поля.
Для плотности энергии
электрического поля
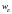 могут быть получены следующие три
формулы:
могут быть получены следующие три
формулы:

Электрический ток. Условие существования тока. Плотность тока. Уравнение непрерывности.
Электрический ток — упорядоченное нескомпенсированное движение свободных электрически заряженных частиц, например, под воздействием электрического поля.
Принято различать три основных вида электрических токов: ток проводимости, ток переноса и ток смещения.
Током проводимости называется ток, образованный направленным движением свободным зарядов в среде под действием внешнего электрического поля. Типичный пример – электрический ток в металлах, образованный направленным движением свободных электронов.
Ток переноса, называемый также конвекционным током, создаётся движущимися заряженными макрочастицами или макроэлементами вещества, например, струёй ионизированного газа, а также потоками свободных заряженных частиц, например, потоком ионов в ускорителях, электронным лучом в кинескопе телевизора.
Ток смещения не связан с движением свободных зарядов.
Для возникновения тока проводимости необходимы два условия: наличие свободных зарядов в веществе и присутствие электрического поля.
Плотность тока это
вектор, направленный в сторону движения
положительных зарядов и численно равный
величине заряда, ежесекундно перемещающегося
через единичную площадку, перпендикулярную
к направлению движения зарядов.
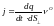 .
.
Выражение
 называется уравнением непрерывности.
Уравнение непрерывности выражает в
дифференциальной форме закон сохранения
заряда. Если заряд в рассматриваемой
точке сохраняется, т.е. не накапливается
и не расходуется, то
называется уравнением непрерывности.
Уравнение непрерывности выражает в
дифференциальной форме закон сохранения
заряда. Если заряд в рассматриваемой
точке сохраняется, т.е. не накапливается
и не расходуется, то ,
,
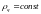 ,
и можно записать:
,
и можно записать:
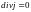 .
Это выражение является необходимым и
достаточным условием стационарности
(постоянства) тока во всех точках среды,
где оно выполняется. Математически это
уравнение означает, что в рассматриваемой
точке нет источников и нет стоков
электрических зарядов.
.
Это выражение является необходимым и
достаточным условием стационарности
(постоянства) тока во всех точках среды,
где оно выполняется. Математически это
уравнение означает, что в рассматриваемой
точке нет источников и нет стоков
электрических зарядов.
В интегральной форме
условие стационарности тока можно
представить в виде:
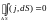 .
Смысл этого выражения в том, что ток,
протекающий через любую замкнутую
поверхность
.
Смысл этого выражения в том, что ток,
протекающий через любую замкнутую
поверхность
 ,
постоянен, если величина входящего
внутрь поверхности потока вектора
,
постоянен, если величина входящего
внутрь поверхности потока вектора
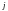 равна выходящему потоку.
равна выходящему потоку.
