43. Колебательный контур.

Колебательный контур – это электрическая цепь, которая содержит активные и реактивные элементы.

Активные элементы (провода и сопротивления) поглощают энергию, реактивные элементы (конденсаторы и катушки индуктивности) преобразуют энергию.

Энергия конденсатора: ,

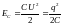Энергия катушки индуктивности: .

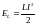Если в эту цепь подать энергию (вывести её из состояния равновесия, то в этой цепи возникнут электромагнитные колебания). Для их описания применим правила Кирхгофа: .

, ,

.

,

,

,

,

,

,

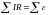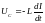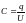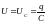
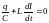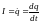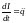
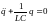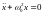
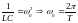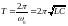
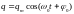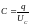
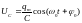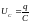
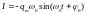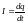
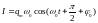, т.е. сила тока опережает по фазе напряжение на .

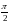(дальше можно не писать)

Рассмотрим пример из области электромагнетизма, а именно – идеальный колебательный контур, состоящий из конденсатора ёмкостью 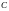и катушки индуктивности . Если зарядить конденсатор и предоставить систему самой себе, то в ней начнется процесс разряда конденсатора через катушку индуктивности. Ток разряда при этом будет изменяться со временем, что приведет к возникновению ЭДС самоиндукции в катушке и, как следствие, к перезарядке конденсатора. Затем снова последует разряд конденсатора и так далее. Таким образом в контуре возникнут незатухающие колебания заряда , тока и напряжения 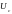. Уравнение, которому будут подчинятся эти колебания, легко получить, используя второе правило Кирхгофа. Если обозначить напряжение на конденсаторе через , а ЭДС самоиндукции через 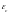, то из указанного закона следует: 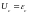. Напряжение на конденсаторе выражается через его заряд и ёмкость в виде 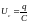, ЭДС самоиндукции в катушке равна 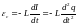, поэтому с учетом равенства: 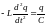или 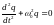, где введено обозначение круговой частоты колебаний в контуре: .

44. Свободные затухающие механические колебания.

45. Затухающие электрические колебания.

46. Вынужденные колебания в электрических цепях. Резонанс колебаний

47. Волны, характеристики волн. Плоская синусоидальная волна. Длина волны. Волновое число.

Волна — изменение состояния среды или физического поля (возмущение), распространяющееся либо колеблющееся в пространстве и времени или в фазовом пространстве. Другими словами, «…волнами или волной называют изменяющееся со временем пространственное чередование максимумов и минимумов любой физической величины — например, плотности вещества, напряжённости электрического поля, температуры».

По своему характеру волны подразделяются на:

По признаку распространения в пространстве: стоячие, бегущие.

По характеру волны: колебательные, уединённые (солитоны).

По типу волн: поперечные, продольные, смешанного типа.

По законам, описывающим волновой процесс: линейные, нелинейные.

По свойствам субстанции: волны в дискретных структурах, волны в непрерывных субстанциях.

По геометрии: сферические (пространственные), одномерные (плоские), спиральные.

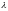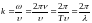Длина волны — расстояние между двумя ближайшими друг к другу точками, колеблющимися в одинаковых фазах, обычно длина волны обозначается греческой буквой . По аналогии с возникающими волнами в воде от брошенного в неё камня — расстояние между двумя соседними гребнями волны. Одна из основных характеристик колебаний. Измеряется в единицах расстояния (метры, сантиметры и т. п.). Величина , обратная длине волны, называется волновым числом и имеет смысл пространственной частоты.

Получить соотношение, связывающее длину волны с фазовой скоростью и частотой можно из определения. Длина волны соответствует пространственому периоду волны, то есть расстоянию, которое точка с постоянной фазой проходит за время, равное периоду колебаний T, поэтому .
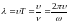