
- •Электростатика и постоянный ток
- •Электрический заряд и его свойства. Закон Кулона.
- •Электрическое поле. Напряженность электростатического поля.
- •Потенциальная энергия взаимодействия. Работа электростатического поля. Потенциал.
- •Связь напряженности электростатического поля и потенциала.
- •Потенциальные диаграммы. Поле заряженной плоскости.
- •Поток вектора напряженности. Теорема Гаусса.
- •Дивергенция вектора напряженности. Истоки и стоки электрического поля.
- •Электрический диполь. Диполь в однородном и неоднородном электрическом поле.
- •Циркуляция вектора напряженности электростатического поля. Интегральное условие потенциальности электростатического поля.
- •Ротор вектора. Дифференциальное условие потенциальности электрического поля.
- •Электроемкость уединенного проводника.
- •Конденсаторы. Плоский и цилиндрический конденсаторы.
- •Диэлектрики. Типы диэлектриков.
- •Поляризация диэлектриков. Вектор поляризации.
- •Свободные и связанные заряды. Диэлектрическая проницаемость среды.
- •Вектор электрического смещения. Теорема Гаусса для поля в веществе.
- •Граничные условия, преломлений линий е и d.
- •Энергия плоского конденсатора. Объемная плотность энергии электростатического поля.
- •Электрический ток. Условие существования тока. Плотность тока. Уравнение непрерывности.
- •Закон Ома для участка цепи и цепи, содержащей эдс. Закон Ома в дифференциальной форме.
- •Закон Джоуля Ленца в интегральной и дифференциальной формах.
- •Сторонние силы. Э.Д.С. Источника тока. Основные закономерности электрических цепей. Правила Кирхгофа.
- •Электрический ток в газах. Процессы ионизации и рекомбинации.
- •Электрический ток в вакууме. Термоэлектронная эмиссия.
- •Электромагнетизм
- •Сила Лоренца. Движение заряженных частиц в электромагнитном поле.
- •Сила Ампера. Рамка с током в магнитном поле. Закон Ампера.
- •Принцип суперпозиции магнитного поля. Закон Био-Савара-Лапласа.
- •Циркуляция вектора магнитной индукции. Закон полного тока.
- •Поток вектора магнитной индукции. Теорема Гаусса для магнитного поля.
- •Работа магнитного поля.
- •Магнитное поле в веществе. Намагниченность.
- •Напряженность магнитного поля. Закон полного тока.
- •Магнетики: диа-, пара-, и ферромагнетики.
- •Электромагнитная индукция. Закон Фарадея для электромагнитной индукции. Правило Ленца.
- •Потокосцепление, самоиндукция. Индуктивность.
- •Токи замыкания и размыкания цепи. Токи Фуко.
- •Система уравнений Максвелла в интегральной и дифференциальной формах.
- •Колебания и волны
- •Характеристики колебательных процессов. Гармонические колебания. Частота и фаза колебаний.
- •Векторная диаграмма гармонических колебаний.
- •Сложение колебаний одинакового направления и одинаковой частоты.
- •Сложение взаимноперпендикулярных колебаний. Фигуры Лиссажу.
- •Гармонические осцилляторы. Пружинный маятник.
- •Колебательный контур.
- •Одномерное волновое уравнение. Групповая скорость, связь ее с фазовой скорость. Дисперсия.
- •Интерференционные полосы равной толщины. Кольца Ньютона.
- •Дифракция волн. Принцип Гюйгенса-Френеля. Метод зон Френеля.
- •Простые задачи дифракции: дифракция на круглом отверстии, на круглом препятствии (по Френелю).
- •Интерферометры. Понятие о голографии.
- •Дифракция на одной щели.
- •Естественный и поляризованный свет. Поляризация света. Закон Малюса.
- •Поляризация при отражении и преломлении на границе диэлектрика. Закон Брюстера.
Сложение взаимноперпендикулярных колебаний. Фигуры Лиссажу.
Рассмотрим результат сложения двух гармонических колебаний одинаковой частоты w, происходящих во взаимно перпендикулярных направлениях вдоль осей х и у. Для простоты начало отсчета выберем так, чтобы начальная фаза первого колебания была равна нулю, и запишем
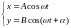 ,
где
— разность фаз обоих колебаний, А
и В
— амплитуды складываемых колебаний.
Уравнение траектории результирующего
колебания находится исключением из
выражений параметра t.
Записывая складываемые колебания в
виде
,
где
— разность фаз обоих колебаний, А
и В
— амплитуды складываемых колебаний.
Уравнение траектории результирующего
колебания находится исключением из
выражений параметра t.
Записывая складываемые колебания в
виде
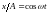 ;
;
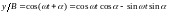 и заменяя во втором уравнении
и заменяя во втором уравнении
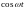 на
на
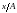 и
и
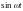 на
на
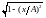 ,
получим после несложных преобразований
уравнение эллипса, оси которого
ориентированы относительно координатных
осей произвольно:
,
получим после несложных преобразований
уравнение эллипса, оси которого
ориентированы относительно координатных
осей произвольно: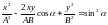 .
.
Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз . Рассмотрим некоторые частные случаи, представляющие физический интерес:
1)
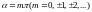 .
В данном случае эллипс вырождается в
отрезок прямой
.
В данном случае эллипс вырождается в
отрезок прямой
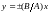 ,
где знак плюс соответствует нулю и
четным значениям
(рис. 205, а), а знак минус — нечетным
значениям
(рис. 205, б). Результирующее колебание
является гармоническим колебанием с
частотой
и амплитудой
,
где знак плюс соответствует нулю и
четным значениям
(рис. 205, а), а знак минус — нечетным
значениям
(рис. 205, б). Результирующее колебание
является гармоническим колебанием с
частотой
и амплитудой
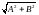 ,
совершающимся вдоль прямой, составляющей
с осью
угол
,
совершающимся вдоль прямой, составляющей
с осью
угол
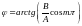 .
В данном случае имеем дело с линейно
поляризованными колебаниями;
.
В данном случае имеем дело с линейно
поляризованными колебаниями;
2)
 .
В этом случае уравнение станет иметь
вид
.
В этом случае уравнение станет иметь
вид
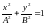 .
Это уравнение эллипса, оси которого
совпадают с осями координат, а его
полуоси равны соответствующим амплитудам
(рис. 206). Кроме того, если А=В, то эллипс
вырождается в окружность. Такие колебания
называются циркулярно
поляризованными колебаниями или
колебаниями, поляризованными по кругу.
.
Это уравнение эллипса, оси которого
совпадают с осями координат, а его
полуоси равны соответствующим амплитудам
(рис. 206). Кроме того, если А=В, то эллипс
вырождается в окружность. Такие колебания
называются циркулярно
поляризованными колебаниями или
колебаниями, поляризованными по кругу.
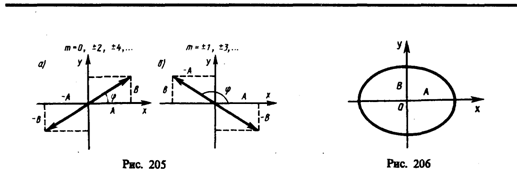
Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний. На рис. 207 представлены фигуры Лиссажу для различных соотношений частот (указаны слева) и разностей фаз (указаны вверху; разность фаз принимается равной j).
О тношение
частот складываемых колебаний равно
отношению числа пересечений фигур
Лиссажу с прямыми, параллельными осям
координат. По виду фигур можно определить
неизвестную частоту по известной или
определить отношение частот складываемых
колебаний. Поэтому анализ фигур Лиссажу
— широко используемый метод исследования
соотношений частот и разности фаз
складываемых колебаний, а также формы
колебаний.
тношение
частот складываемых колебаний равно
отношению числа пересечений фигур
Лиссажу с прямыми, параллельными осям
координат. По виду фигур можно определить
неизвестную частоту по известной или
определить отношение частот складываемых
колебаний. Поэтому анализ фигур Лиссажу
— широко используемый метод исследования
соотношений частот и разности фаз
складываемых колебаний, а также формы
колебаний.
Гармонические осцилляторы. Пружинный маятник.
Гармонический
осциллятор (в классической механике) —
это система, которая при смещении из
положения равновесия испытывает действие
возвращающей силы
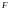 ,
пропорциональной смещению
(согласно закону Гука):
,
пропорциональной смещению
(согласно закону Гука):
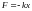
где —
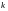 коэффициент жёсткости системы.
коэффициент жёсткости системы.
Если — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.
Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
Пружинный маятник.
Допустим, что груз
вертикально подвешен на пружине. В
состоянии равновесия сила тяжести,
действующая на груз, уравновешивается
силой упругости пружины и можно
записать: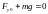 .
Если спроектировать это выражение на
вертикальную ось
,
то получим:
.
Если спроектировать это выражение на
вертикальную ось
,
то получим:
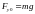 .
Здесь сила упругости
.
Здесь сила упругости
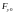 определяется удлинением пружины
определяется удлинением пружины
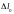 .
При движении второй закон Ньютона может
быть представлен в векторном виде:
.
При движении второй закон Ньютона может
быть представлен в векторном виде:
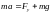 ,
или в проекциях на ось
:
,
или в проекциях на ось
:
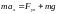 .
Обозначим текущее смещение тела из
положения равновесия через
и, учитывая его малость, запишем для
проекции силы упругости выражение
.
Обозначим текущее смещение тела из
положения равновесия через
и, учитывая его малость, запишем для
проекции силы упругости выражение
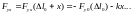 .
Очевидно, что при этом мы фактически
используем закон Гука. Величина
.
Очевидно, что при этом мы фактически
используем закон Гука. Величина
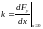 называется жесткостью пружины. Используя
три последних выражения, получаем
дифференциальное уравнение гармонических
колебаний в канонической форме:
называется жесткостью пружины. Используя
три последних выражения, получаем
дифференциальное уравнение гармонических
колебаний в канонической форме:
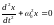 ,
где
,
где
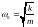 - собственная круговая частота колебаний
груза.
- собственная круговая частота колебаний
груза.
