39. Векторная диаграмма гармонических колебаний.

Решение многих вопросов, в частности, сложение нескольких колебаний одинакового направления, облегчается и становится наглядным, если изображать колебания графически в виде вектора на плоскости.

(это надо постараться нарисовать). Из точки 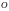, взятой на оси , отложим вектор, модуль которого равен , образующий с осью угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца вектора будет перемещаться по оси в пределах от 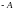до 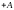, причем координата этой проекции будет изменяться со временем по закону . Следовательно, проекция вектора на ось будет совершать гармоническое колебание с амплитудой, равной длине вектора. Круговая частота будет равна угловой скорости вращения вектора, а начальная фаза – углу, образуемому вектором с осью при . Из этого следует, что гармоническое колебание может быть задано с помощью вектора, длина которого равна амплитуде колебания, а направление вектора образует с осью угол, равный начальной фазе колебаний.

40. Сложение колебаний одинакового направления и одинаковой частоты.

Рассмотрим сложение двух гармонических колебаний одинакового направления и одинаковой частоты. Пусть уравнения этих колебаний имеют вид: 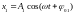, 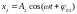. Представим эти колебания с помощью векторов 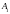и 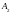на векторной диаграмме.

Построим по правилам сложения векторов результирующий вектор . Видно, что проекция этого вектора на ось равна сумме проекций слагаемых векторов. 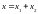. Поэтому вектор представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью , как и векторы и , так что результирующее движение будет гармоническим колебанием с частотой , амплитудой и начальной фазой , т.е. можно записать: 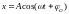, где, как видно из построения: , .

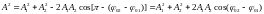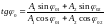Таким образом, метод векторной диаграммы позволяет свести сложение нескольких гармонических колебаний одной частоты к операции сложения векторов.

Если разность фаз обоих колебаний 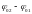равна нулю или кратна четному числу , то амплитуда результирующего колебания будет равна сумме 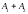, т.е. колебания взаимно усиливают друг друга. Если разность фаз равна или кратна нечетному числу , то амплитуда результирующего колебания будет равна по модулю разности амплитуд 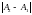. Иными словами, колебания взаимно ослабляют друг друга.

Если складываются колебания одинакового направления, мало отличающиеся по частоте, то результирующее колебание можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такие колебания называются биениями.

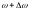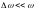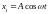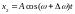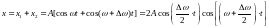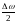Итак, допустим, есть два гармонических колебания с круговыми частотами и , причем . Предположим что амплитуды этих колебаний одинаковы, а начальные фазы равны нулю. Тогда уравнения этих колебаний будут иметь вид: , . Сложим эти выражения и применим тригонометрическую формулу для суммы косинусов: . Воспользуемся начальным условием и пренебрежём членом . Окончательно имеем: .

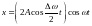Частота пульсаций амплитуды равна разности частот складываемых колебаний.