2.2.1. Расчет прочности по нормальному сечению

Проверяем условие положения границы сжатой зоны:

M_ceч=R_b× b'_f × (h₀-0,5×h'_f)=

=7,65×1610×50×(415-0,5×50)=

=234×10³ кН×мм > М=72,3×10³кН×мм.

Следовательно, граница сжатой зоны проходит в полке.

Расчет прочности производим как расчет прочности балки прямоугольного сечения шириной полки b'_f=1610 мм:

α_m=M/(R_b× b'_f× h_o²)=72,3×10⁶/(7,65× 1610 ×415²)=0,034 < 0,39

A_s= R_b×b'_f ×h₀ (1- √(1-2× α_m)) / R_s= 7,65×1610 ×415 (1-√(1-2× 0,034))/355=504 мм^2..Принимаем ( по таблице 3 сортамента арматуры) 2Ø 18 А400 с A_s=509 мм². В каждом продольном ребре по одному диаметру 18 мм класса А400.

2.2.2. Расчет прочности по наклонному сечению

Проверяем достаточность принятых сечений расчетом прочности по наклонному сечению (прочность бетонной полосы). Ширина b=180 мм (ширина сечения 2-х ребер, см.рис.3).

Q_ceч=0,3×R_b×b×h₀=

=0,3×,65×80×415=

=171,4×10³ H>Q=52,7×10³ H (см.стр.7),

т.е. прочность полосы обеспечена.

Диаметр хомутов принимаем в зависимости от диаметра продольной арматуры (из условия свариваемости).

d_sw=l/3×d_s (d_s- диаметр продольной рабочей арматуры) d_s=18 мм; принимаем d_sw=6 мм класса А240 с R_sw=170 МПа. По конструктивным требованиям шаг хомутов S_w при h ≤450 мм 1/2 h=225 мм и не более 150 мм принимаем S_w=150 мм.

Расчет изгибаемых элементов по наклонному сечению производим по условию: Q < Q_b+Q_Sw,

где Q-поперечная сила в наклонном сечении;

Q_b- поперечная сила, воспринимаемая бетоном в наклонном сечении:

Q_b=M_b/c, M_b=l,5*R_bt×b×h₀²=

= 1,5 ×0,675×180×415²=31,4×10⁶ Н×мм

Q_sw- поперечная сила, воспринимаемая хомутами в наклонном сечении:

Q_sw=0,75 × q_sw × с;

Площадь сечения одного хомута d_sw = 6мм по сортаменту A_swt = 28,3 мм; для двух хомутов (по одному в каждом ребре) A_sw= 57,0 мм. При принятом шаге хомутов S_w =150 мм интенсивность хомутов составляет:

q_sw=R_sw × A_sw / S_w=

=170 × 57/ 150 =64,6 Н/мм

Расстояние С от опоры принимаем максимально допустимое:

С= 2 × h_o=2×415= 830 мм, но более S_w =150 мм

Q_b = M_b / S_w= 31,4×10⁶/150= 209×10⁶ Н=209 кН

Принимаем наименьшее значение S_w= 150 мм, (см.лист 4).

Q_sw=0,75 ×q_sw ×S_w=0,75× 64,6×150=7267,5 Н=7,26 кН

Q_b+Q_sw= 206+7,26=213,2 кН > Q=52,7 кН.

Прочность наклонных сечений обеспечена.

3. Расчет разрезного ригеля p-2

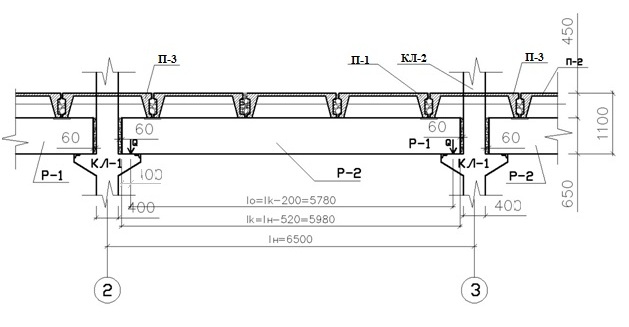
Рис.4. Расчетная схема

1_Н- номинальная длина (см. приложение лист 1,2);

1_К- конструктивная длина (см. приложение лист 5,6);

1_О- расчетный пролет.

Для расчета принимаем ригель как разрезной прямоугольного сечения размерами b×h = 300x650 мм.

3.1. Сбор нагрузок

Расчетная нагрузка:

а) От веса перекрытия (q ×1_н)/b_н= (19,2 × 5,64)/1,626= 66,59 кН/м;

q- полная расчетная нагрузка, приходящая 1 п.м плиты ( из расчета продольного ребра, стр.7).

1_н - номинальная длина плиты ;

b_н - номинальная ширина плиты;

б) от веса ригеля: 25 ×0,3 × 0,65 ×1,1 = 5,36 кН/м

Суммарная нагрузка:

q= 66,59+ 5,36 = 71,95 кН/м

Изгибающий момент:

М= (q × 1_о²)/8=(71,95×5,78²)/8=300,4 кН×м

Q= (q × 1_о)/2 = (71,95 × 5,18)/2= 208 кН

Для расчета принимаем:

Бетон класса В20 с R_B= 11,5 МПа, R_B= γ_в1 × R_B=0,9 × 11,5 = 10,35 МПа

R_Bt= 0,9 МПа, R_Bt= γ_Bt ×R_Bt= 0,9 × 0,9= 0,81 МПа.

γ_Bt - учитывает длительность действия нагрузки, коэффициент условия работы.

Продольная арматура класса А400 с R_s= 355 МПа; Поперечная арматура класса А240 с R_sw= 170 МПа;