
Программа
#include<iostream.h>
#include<stdio.h>
#include<conio.h>
#include<math.h>
void main()
{clrscr();
int i, n=15, A[15];
FILE *f1;
f1=fopen("F.txt","r");
int max, min, minp, maxmn, r, s;
for(i=0;i<n;i++)
fscanf(f1,"%d",&A[i]);
fclose(f1);
max=A[0];
min=A[0];
maxmn=A[0];
minp=A[1];
for(i=0;i<n;i++)
{if(pow(-1,i+1)<0 && abs(maxmn)<abs(A[i])) maxmn=A[i];
else if(minp>A[i]) minp=A[i];
if(max<A[i]) max=A[i];
if(min>A[i]) min=A[i];}
r=A[0]-A[n-1];
s=max+min;
cout<<"Ishodnuy vektor\n";
for(i=0;i<n;i++)
cout<<A[i]<<"\t";
cout<<"\nmax="<<max<<" minp="<<minp<<" maxmn="<<maxmn<<" s="<<s<<" r="<<r;}
Результат
Ishodnuy vector
3 -6 7 1 -3 0 4 8 -1 6
2 7 -9 3 1
max=8 minp=-6 maxmn=-9 s=-1 r=2
Задание 7
Дано: Схема и параметры. Найти: Токи на сопротивлениях;
и показания вольтметра
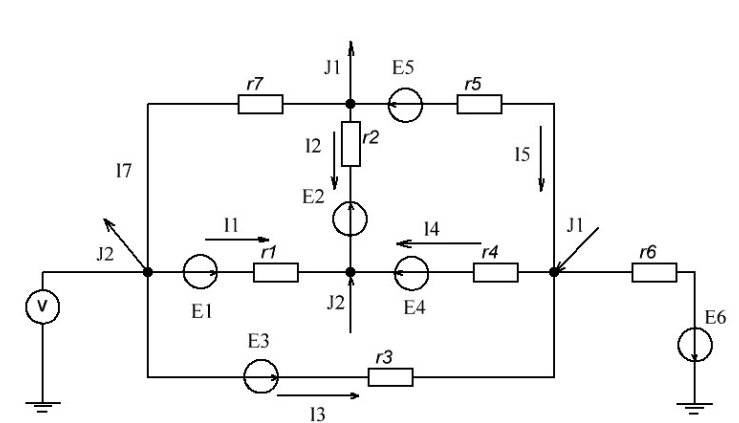
Параметры схемы:
E1:= 60 E2:= 40 E3:= 30 E4:= 20 E5:= 50 E6:= 20
r1:= 6 r2:= 4 r3:= 5 r4:= 4 r5:= 5 r6:= 8 r7:= 3
J1:=3 J2:=5
Метод контурных токов
Найдем эквивалентные значения ЭДС
e1:= E1 + J2 r1 e1:= 90 r13:= r1 r32:= r4
e5:= E5 J1 r5 e5:=35 r31:= r1
r11:= r1 + r2 + r7 r12:= r2
r22:= r5 + r4 + r2 r21:= r2
r33:= r1 + r4 + r3 r23:= r4
Система уравнений составленных методом контурных токов:
I11r11 I22r12 I33r13 = E2 e1
I11r21 + I22r22 I33r23 = e5 + E4 + E2
I11r31 I22r32 + I33r33 = e1 E4 E3
Составляем определитель и решаем его методом Крамара:
R
=
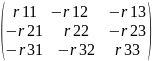 E =
E =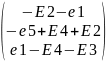
R
=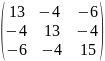 E
=
E
=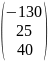
I=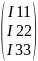 I
=
I
=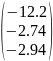
После определения токов контуров найдем остальные токи в схеме:
I1:= I11 I33 J2 I1 = 4.257
I2:= I11 I22 I2 = 9.464
I3:= I33 I3 = 2.943
I4:= I22 I33 I4 = 0.207
I5:= I22 + J1 I5 = 5.737
I7:= I11 I7 = 12.2
Метод узловых потенциалов
Находим сумму сопротивлений проводимости узлов и смежных с узлами сопротивлений:
Gaa:
=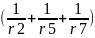 Gab: =
Gab: =
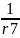 Gca: =
Gca: =
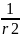
Gbb
:=
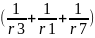 Gac :=
Gbc :=
Gac :=
Gbc :=
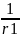
Gcc:
=
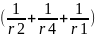 Gba: =
Gcb :=
Gba: =
Gcb :=
Найдем токи веток которые входят в узлы:
Ia
:=
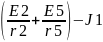 Ib: =
Ib: =
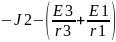
Ic
:=
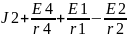
Составляем систему уравнений, из которой мы найдем потенциалы узлов:
Va
(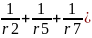
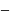 Vb
Vb
 Vc
Vc
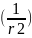 =
=
─ Va
+ Vb
─
Vc (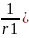 =
=
─ Va
─
Vb
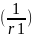 + Vc
=
+ Vc
=
Составим определитель и найдем решение методом Крамара:
V
=
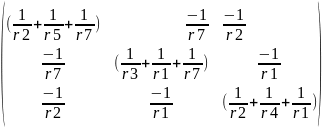
I
=
Результаты подстановки и решения матрицы:
V
=
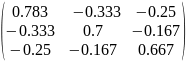 I
=
I
=
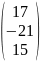
Полученные потенциалы точек равны:
V
=
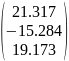
I1:
=
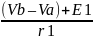 I2:
=
I2:
=
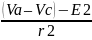
I3
:=
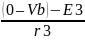 I4:
=
I4:
=
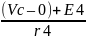
I5
:=
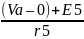 I7:
=
I7:
=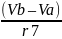
Результаты полученных токов:
I1 = 4.257 I4 = 0.207
I2 = 9.464 I5 = 5.737
I3 = 2.943 I7 = 12.2
S1:= I12∙ r1 + I22 ∙r2 + I32 ∙r3 + I42∙ r4 + I52∙ r5 + I72∙ r7
S2:= E1∙ I1 – E2∙ I2 + E3∙ I3 + E4∙ I4 – E5∙ I5 – J1∙ Va + J2∙ (Vb – Va)
S1:= 1.122 × 103
S2:= 1.122 × 103
Определим напряжение на вольтметре:
V:= Va – 0 –E6 V = - 35.284
