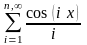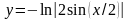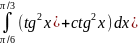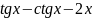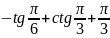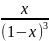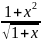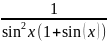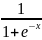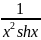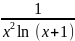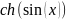Министерство образования и науки Украины
Национальный горный университет
Институт электроэнергетики
Кафедра электропривода
Отчет
По учебной практике
Вариант 2
Выполнил:
Студент группы ЕМС-12-1
Башкирцев Р.В
Проверил:
Проф. Воскобойник В.Э
Асс. Твердохлебов В.В
Днепропетровск
2013 год
СОДЕРЖАНИЕ
Задание 1. Суммирование функциональных рядов____________________
Задание 2. Вычисление определенного интегралов____________________
Задание 3. Операции с массивами__________________________________
Задание 4. Табулирование функции_________________________________
Задание 5.Сортировка массивов____________________________________
Задание 6. Операции с файлами____________________________________
Задание 7. Расчет разветвленной электрической цепи при
постоянном токе_________________________________________________
Задание 1. Суммирование функциональных рядов
Условие
Составить алгоритм и программу вычисления
- Значение функциональной суммы своего варианта для количества членов от одного до (n) слагаемых;
- Значение суммы с нужной точностью э = 0.001. Найти также количество просуммированных элементов;
- Значение функции согласно с формулой;
№ |
Функциональные ряды |
Диапазон Изменения аргумента |
n |
Функция |
2 |
|
[/5; 9/5] |
16 |
|
Блок схема часть 1
Начало
m

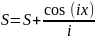

j<=1, 3, 1
x
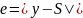


вывод
од
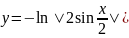
X, y, S, e
S<=0


конец i
i<=1, 16, 1
конец j
Конец
m![]()
Таблица символических имен
Имя |
Значения |
Тип |
Данные |
i |
Индекс элемента |
Целый |
Вычисляется |
j |
Счетчик цикла |
Целый |
Вычисляется |
S |
Сумма ряда |
Действительный |
Вычисляется |
y |
Функция |
Действительный |
Вычисляется |
x |
Аргумент |
Действительный |
Задается |
Вычисление конечной суммы
#include<iostream.h>
#include<math.h>
#include<stdio.h>
#include<conio.h>
void main()
{
int i, j;
double S, x, y, e;
clrscr();
for(j=0;j<3;j++)
{
cout<<"x=";
cin>>x;
y=-log(fabs(2*sin(x/2)));
S=0;
for(i=1;i<=16;i++)
S=S+cos(i*x)/i;
e=fabs(y-S);
cout<<"y="<<y<<" S="<<S<<" e="<<e<<endl;
}
getch();
}
Б
m
лок схема часть 2Начало
j<=1, 3, 1
вывод
i, S, y
x
Да
Нет
S<=0
Конец
i<=1
m
Таблица символических имен
Имя |
Значения |
Тип |
Данные |
i |
Индекс элемента |
Целый |
Вычисляется |
j |
Счетчик цикла |
Целый |
Вычисляется |
S |
Сумма ряда |
Действительный |
Вычисляется |
y |
Функция |
Действительный |
Вычисляется |
x |
Аргумент |
Действительный |
Задается |
e |
Погрешность |
Действительный |
Вычисляется |
Вычисление суммы с заданной точностью
#include<iostream.h>
#include<math.h>
#include<conio.h>
#include<stdio.h>
void main()
{
clrscr();
int i, j;
float S, y, x;
for(j=0;j<3;j++)
{
cout<<"\nVvedite x ot pi/5 do 9pi/5\nx=";
cin>>x;
cout<<endl;
y=-log(fabs(2*sin(x/2)));
S=0;
i=1;
cout<<"\nn S y";
do
{
S=S+cos(i*x)/i;
cout.precision(10);
cout<<endl<<i<<"\t"<<S<<"\t"<<y;
i++;
}
while(fabs(y-S)>=0.001);
}
getch();
}
Результат конечной суммы
x= 0.628
y= 0.481702 S= 0.481702 e= 0.072595
x= 2.321
y= -0.606502 S= -0.588296 e= 0.018206
x= 5.652
y= 0.476811 S= 0.401281 e= 0.07553
Результат суммы с заданной точностью
Vvedite x ot pi/5 do 9pi/5
i S y
1 0.4771620333 0.4817020893
2 0.4795806408 0.4817020893
3 0.4827907383 0.4817020893
4 0.4855662286 0.4817020893
5 0.4868541956 0.4817020893
6 0.4861742556 0.4817020893
7 0.4837975502 0.4817020893
8 0.4806389213 0.4817020893
9 0.4779047966 0.4817020893
10 0.4766325355 0.4817020893
11 0.4772968888 0.4817020893
12 0.4796330333 0.4817020893
Vvedite x ot pi/5 do 9pi/5
i S y
1 -0.6430189013 -0.6065022945
2 -0.5592246056 -0.6065022945
3 -0.6352359056 -0.6065022945
4 -0.6104645133 -0.6065022945
5 -0.5766769648 -0.6065022945
6 -0.641145885 -0.6065022945
7 -0.5882959366 -0.6065022945
8 -0.5992373228 -0.6065022945
9 -0.6321244836 -0.6065022945
10 -0.5798509121 -0.6065022945
11 -0.6179678864 -0.6065022945
12 -0.6157627702 -0.6065022945
13 -0.5839809775 -0.6065022945
14 -0.6274466515 -0.6065022945
Vvedite x ot pi/5 do 9pi/5
i S y
1 0.4663950205 0.476810962
2 0.45767349 0.476810962
3 0.4564620852 0.476810962
4 0.4630290568 0.476810962
5 0.4746789634 0.476810962
6 0.4868516624 0.476810962
7 0.4949014783 0.476810962
8 0.4958648682 0.476810962
9 0.4895458221 0.476810962
10 0.4785237312 0.476810962
11 0.4671065807 0.476810962
12 0.4596519172 0.476810962
13 0.4589082301 0.476810962
14 0.4650063217 0.476810962
15 0.4754689634 0.476810962
16 0.4862122834 0.476810962
17 0.4931357205 0.476810962
18 0.48778373 0.476810962
19 0.477823019 0.476810962
20 0.4676848682 0.476810962
Задание 2. Вычисление определенного интеграла
Условие
Составить схему алгоритма и программу для вычислений:
- Определенного интеграла методом Трапеции;
- Определение интеграла методом Ньютона-Лейбница
№ |
Интеграл |
Метод |
Число областей интегрирования |
Первообразная функции |
2 |
|
Трапеции |
54 |
|
Блок схема
Начало
s
a<= pi/6;
b<= pi/3;
n<=54;
i<=1, n-1, 1
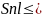
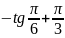 )-
)-
)
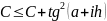
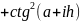
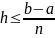
Конец i
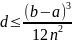
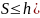
C<=0
p
s
p
d
вывод
S, Snl
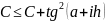
Конец i
C<=0
v
i<=1, n-1, 1
d
m
v
m
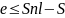
вывод
n, S, Snl, e
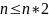
e ≥ 0.001
Нет
Да
Конец
Таблица символических имен
Имя |
Значения |
Тип |
Данные |
a |
Нижний предел |
Действительный |
Задается |
b |
Верхний предел |
Действительный |
Задается |
h |
Шаг интегриров. |
Действительный |
Вычисляется |
d |
Погрешность |
Действительный |
Вычисляется |
S |
Интеграл |
Действительный |
Задается |
Snl |
Интеграл вычеслен по формуле Ньютона-Лейбница |
Действительный |
Вычисляется |
C1 |
Сумма |
Действительный |
Вычисляется |
C2 |
Сумма |
Действительный |
Вычисляется |
E |
Погрешность |
Действительный |
Вычисляется |
n |
Индекс |
Целый |
Задается |
i |
|
Целый |
Вычисляется |
Вычисление определенного интеграла
#include<iostream.h>
#include<math.h>
#include<conio.h>
#include<stdio.h>
void main()
{
float h, d, S, Snl, C, pi=3.1415, a=pi/6, b=pi/3, e;
int n=54, i;
clrscr();
Snl=(tan(b)-1/tan(b)-2*b-tan(pi/6)+1/tan(pi/6)+pi/3)-
(tan(a)-1/tan(a)-2*a-tan(pi/6)+1/tan(pi/6)+pi/3);
h=(b-a)/n;
d=pow(b-a,3)/(12*n*n);
C=0;
for(i=1;i<=n-1;i++)
C+=pow(tan(a+i*h),2)+pow(1/tan(a+i*h),2);
S=h*((pow(tan(a),2)+pow(1/tan(a),2)+pow(tan(b),2)+pow(1/tan(b),2))/2+C)+d;
cout<<"y=tan(x)-1/tan(x)-2*x-tan(pi/6)+1/tan(pi/6)+pi/3";
cout<<"\nf(x)=pow(tan(x),2)+pow(1/tan(x),2)";
cout<<"\na=pi/6 b=pi/3\n";
cout<<"\nMetod Trapezuu";
cout<<"\nS="<<S<<endl;
cout<<"\nFormyla Nuytona-Leubucha";
cout<<"\nSnl="<<Snl<<endl;
cout<<"\nRashet s toshnostuy e=0.001\n";
cout<<"\nn S Snl e\n";
n=15;
do
{
h=(b-a)/n;
d=pow(b-a,3)/(12*n*n);
C=0;
for(i=1;i<=n-1;i++)
C+=pow(tan(a+i*h),2)+pow(1/tan(a+i*h),2);
S=h*((pow(tan(a),2)+pow(1/tan(a),2)+pow(tan(b),2)+pow(1/tan(b),2))/2+C)+d;
cout.precision(5);
e=fabs(Snl-S);
cout<<n<<"\t"<<S<<"\t\t"<<Snl<<"\t\t"<<e<<endl;
n=n*2;
}
while(fabs(Snl-S)>=0.001);
getch();
}
Результат вычислений определенного интеграла
y=tan(x)-1/tan(x)-2*x-tan(pi/6)+1/tan(pi/6)+pi/2
f(x)=pow(tan(x),2)+pow(1/tan(x),2)
a=pi/6 b=pi/3
Metod Trapezuu
S = 1.262341
Formyla Nuytona-Leubucha
Snl = 1.262152
Rashet s tochnostuy e = 0.001
n S y e
15 1.2647 1.26215 0.00255
30 1.26279 1.26215 0.00064
Задание 3. Операции с массивами
Условие
Сложить
схему алгоритма и программу для вычисления
элементов матрицы
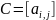 ,
что является произведением матрицы
,
что является произведением матрицы
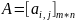 на матрицу
на матрицу
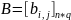 . Каждый элемент матрицы С вычисляется
за формулой
. Каждый элемент матрицы С вычисляется
за формулой
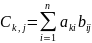
i=1, 2,…n; j=1, 2,…q; k=1, 2,…m (n ≤ 6, q ≤ 8, m ≤ 10)
Выходные данные: m= 3; n= 4; q=3;
A
=
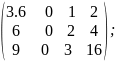 B
=
B
=
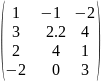
Б лок схема
Начало
m
m<= 3
n<= 4
q<=3
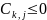
m
k
i<= 1, n, 1
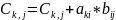
k<= 1, m, 1
j<= 1, q, 1
Конец i
Конец j
Конец k
k
вывод
A, B, C
Конец
Таблица символических имен
Имя |
Значения |
Тип |
Данные |
k |
Номер элемента вектора |
Целый |
Вычисляется |
i |
Индекс вектора |
Целый |
Вычисляется |
n |
Кол-во елементов вектора |
Целый |
Задается |
m |
Множитель |
Действительный |
Вычисляется |
x |
Заданый вектор |
Действительный |
Задается |
y |
Заданый вектор |
Действительный |
Задается |
z |
Искомый вектор |
Действительный |
Вычисляется |
Программа
#include<iostream.h>
#include<math.h>
#include<conio.h>
#include<stdio.h>
void main()
{
clrscr();
int m=3, n=4, g=3, j, k, i;
float A[3][4]= {3.6, 0, 1, 2,
6, 0, 2, 4,
9, 0, 3, 16};
float B[4][3]= {1, -1, -2,
3, 2.2, 4,
2, 4, 1,
-2, 0, 3};
float C[3][3];
for(k=0;k<m;k++)
for(j=0;j<g;j++)
{
C[k][j]=0;
for(i=0;i<n;i++)
C[k][j]+=A[k][i]*B[i][j];
}
cout<<"Matrica A\n";
for(k=0;k<m;k++)
{
for(i=0;i<n;i++)
cout<<A[k][i]<<"\t";
cout<<endl;
}
cout<<"\nMatrica B\n";
for(i=0;i<n;i++)
{
for(j=0;j<g;j++)
cout<<B[i][j]<<"\t";
cout<<endl;
}
cout<<"\nMatrica C=A*B\n";
for(k=0;k<m;k++)
{
for(j=0;j<g;j++)
cout<<C[k][j]<<"\t";
cout<<endl;
}
}
Результаты вычислений
Matrica A
3.6 0 1 2
6 0 2 4
9 0 3 16
Matrica B
1 -1 -2
3 2.2 4
2 4 1
Matrica C=A*B
1.6 0.4 -0.2
2 2 2
-17 3 33
Задание 4. Табулирование функции
Условие
Составить алгоритм и программу вычислении функции своего варианта и вывести их результат в виде таблицы.
№ |
Алгебр. рац |
Алгебр. иррац |
Тригоном. |
Показ |
Гипербол |
Натурал .логарифм |
Соединение Тригоном.Гипербол. и им обратных |
2 |
|
|
|
|
|
|
|
Блок схема часть 1
F1
x = - 1
return 0
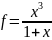
return f
F1
F2
x ≤ 1
return 0
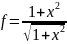
return f
F2
Нет
Да
Нет
Да
F3
return 0
F3
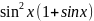 =0
=0
Нет
Да
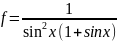
return f
F4
1+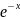 =0
=0
return 0
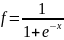
return f
F4
Нет
Да
F5
return 0
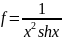
return f
F5
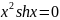
Нет
Да
F6
return 0
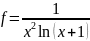
return f
F6
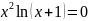
Нет
Да
F7
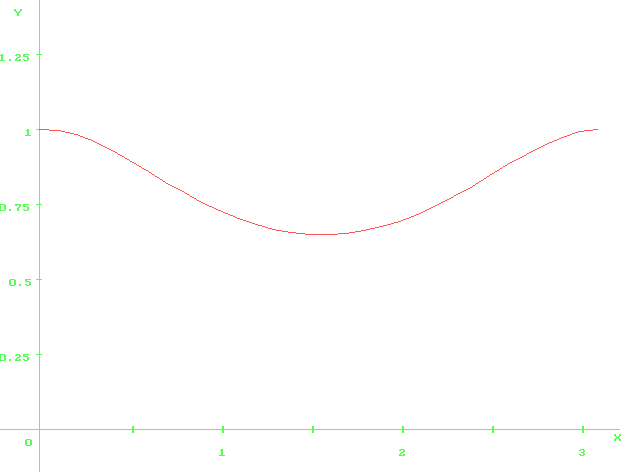
ch(sinx)=0
return 0
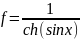
return f
F7
Нет
Да
Начало
ввод
S, Snl

F1
F1
z
z
L

i<= 1, 30, 1
F2
вывод

x, F1, F2, F3, F4, F5, F6, F7
F3

F4
Конец i

F5
конец
Конец
x, F1, F2, F3, F4, F5, F6,F7

F6

F7
конец
L
Таблица символических имен
Имя |
Значения |
Тип |
Данные |
pi |
Число пи |
Действительный |
Константа |
x |
Аргумент |
Действительный |
Задается |
f |
Функция |
Действительный |
Вычисляется |
i |
Шаг цикла |
Целый |
Вычисляется |
Программа табулирования функций
#include<iostream.h>
#include<math.h>
#include<stdio.h>
#include<conio.h>
#include<iomanip.h>
float F1(float x)
{
float f;
if(x==-1) return 0;
else
{
f=(pow(x,3)/(1+x));
return f;
}
}
float F2(float x)
{
float f;
if(x<=1) return 0;
else
{
f=(1+x*x)/sqrt(1+x);
return f;
}
}
float F3 (float x)
{
float f;
if(pow(sin(x),2)*(1+sin(x))==0) return 0;
else
{
f=1/(pow(sin(x),2)*(1+sin(x)));
return f;
}
}
float F4 (float x)
{
float f;
if(1+exp(-x)==0) return 0;
else
{
f=1/(1+exp(-x));
return f;
}
}
float F5 (float x)
{
float f;
if(x*x*sinh(x)==0) return 0;
else
{
f=1/(x*x*sinh(x));
return f;
}
}
float F6 (float x)
{
float f;
if(x*x*log(x+1)==0) return 0;
else
{
f=1/(x*x*log(x+1));
return f;
}
}
float F7 (float x)
{
float f;
if(cosh(sin(x))==0) return 0;
else
{
f=1/cosh(sin(x));
return f;
}
}
void main()
{
clrscr();
const float pi=3.1415;
float x[]={0,0.1,0.2,0.3,0.4,0.5,pi/4,0.8,0.9,1,pi/3,1.1,1.2,
1.3,1.4,1.5,1.6,1.7,1.8,1.9,2,2.1,2.2,2.3,2.4,2.5,2.6,2.8,2.9,3,pi};
int i;
cout<<setw(5)<<"x"<<setw(10)<<"F1"<<setw(10)<<"F2"
<<setw(10)<<"F3"<<setw(10)<<"F4"<<setw(10)<<"F5"
<<setw(10)<<"F6"<<setw(10)<<"F7\n\n";
for(i=0;i<=30;i++)
{
cout<<setw(5)<<x[i]
<<setw(10)<<setprecision(3)<<F1(x[i])
<<setw(10)<<setprecision(3)<<F2(x[i])
<<setw(10)<<setprecision(3)<<F3(x[i])
<<setw(10)<<setprecision(3)<<F4(x[i])
<<setw(10)<<setprecision(3)<<F5(x[i])
<<setw(10)<<setprecision(3)<<F6(x[i])
<<setw(10)<<setprecision(3)<<F7(x[i])
<<endl;
getch();}
getch();
}
Блок схема часть 2
koordinat
Line(0,430,620,430)
Line(40,0,40,480)
koordinat
Начало
f
r <= DETECT
x1 <= 0.1∙ (i-1)

mx <= 180
x2 <= 0.1∙i
koordinat ( )
ch(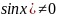
Нет
my <= 300
f
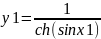
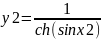
j
Да
i <=1, 3, 1
a
j
Line(x1∙mx+40,430 – y1∙my,x2∙mx+40,430 – y2∙my
Конец
Конец i
a
Таблица символических имен
Имя |
Значения |
Тип |
Данные |
i |
Счетчик цикла |
Целый |
Вычисляется |
x1 |
Первая координата по x |
Действительный |
Вычисляется |
x2 |
Вторая координата по x |
Действительный |
Вычисляется |
y1 |
Первая координата по y |
Действительный |
Вычисляется |
y2 |
Вторая координата по y |
Действительный |
Вычисляется |
mx |
Масштаб по x |
Действительный |
Задано |
my |
Масштаб по y |
Действительный |
Задано |
Программа построения графика функции
#include<iostream.h>
#include<conio.h>
#include<process.h>
#include<graphics.h>
#include<time.h>
#include<math.h>
void koordinat()
{
line(0,430,620,430);
line(40,0,40,480);
}
void main()
{
clrscr();
int r, d;
r=DETECT;
initgraph(&r,&d,"c:\\borlandc\\bgi");
setbkcolor(15);
setcolor(10);
koordinat();
outtextxy(15,10,"Y");
outtextxy(615,435,"X");
for(int j=0;j<=560;j=j+90)
outtextxy(130+j,427,"|");
for(j=25;j<=430;j=j+75)
outtextxy(37,27+j,"-");
setcolor(10);
outtextxy(10,280,"0.5");
outtextxy(0,55,"1.25");
outtextxy(26,130,"1");
outtextxy(0,205,"0.75");
outtextxy(0,355,"0.25");
outtextxy(220,450,"1");
outtextxy(400,450,"2");
outtextxy(580,450,"3");
outtextxy(26,440,"0");
float mx, my, y1, x1, y2, x2;
mx=(180);
my=(300);
setcolor(12);
for(int i=1;i<=31;i++)
{
x1=0.1*(i-1);
x2=0.1*i;
if(cos(sin(x1))!=0)
{
y1=1/cosh(sin(x1));
y2=1/cosh(sin(x2));
line(ceil(x1*mx)+40,430-ceil(y1*my),ceil(x2*mx)+40,430-ceil(y2*my));
}
}
closegraph;
getch();
}
Результат табулирования функций
x F1 F2 F3 F4 F5 F6 F7
0 0 0 0 0.5 0 0 1
0.1 0 0 91.227 0.525 998.335 1049.206 0.995
0.2 0.007 0 21.137 0.55 124.171 137.12 0.981
0.3 0.021 0 8.839 0.574 36.487 42.35 0.958
0.4 0.046 0 4.746 0.599 15.216 18.575 0.929
0.5 0.083 0 2.941 0.662 7.676 9.865 0.895
0.785 0.271 0 1.172 0.687 1.866 2.797 0.793
0.8 0.284 0 1.132 0.69 1.759 2.658 0.788
0.9 0.5 0 0.914 0.711 1.203 1.923 0.756
1 0.5 0 0.767 0.731 0.851 1.443 0.727
1.047 0.561 1.465 0.715 0.74 0.73 1.273 0.715
1.1 0.634 1.525 0.666 0.75 0.619 1.114 0.702
1.2 0.785 1.645 0.596 0.769 0.46 0.881 0.682
1.3 0.955 1.774 0.549 0.786 0.348 0.71 0.666
1.4 1.143 1.911 0.519 0.802 0.268 0.583 0.655
1.5 1.35 2.055 0.503 0.818 0.209 0.485 0.649
1.6 1.575 2.208 0.501 0.832 0.164 0.409 0.648
1.7 1.82 2.367 0.511 0.846 0.131 0.348 0.652
1.8 2.083 2.534 0.534 0.858 0.105 0.3 0.661
1.9 2.365 2.707 0.574 0.87 0.085 0.26 0.675
2 2.667 2.887 0.633 0.881 0.069 0.228 0.693
2.1 2.987 3.073 0.72 0.891 0.056 0.2 0.716
2.2 3.328 3.265 0.846 0.9 0.046 0.178 0.743
2.3 3.687 3.463 1.03 0.909 0.038 0.158 0.774
2.4 4.066 3.666 1.308 0.917 0.032 1.142 0.808
2.5 4.464 3.875 1.747 0.924 0.026 0.128 0.844
2.6 4.882 4.09 2.483 0.931 0.022 0.115 0.88
2.8 5.777 4.535 6.675 0.943 0.016 0.096 0.946
2.9 6.254 4.765 14.097 0.948 0.013 0.087 0.972
3 6.75 5 44.004 0.953 0.011 0.08 0.99
3.141 7.486 5.341 1.164e+08 0.959 0.009 0.071 1
Результат графика функции
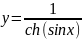
Задание 5. Сортировка массивов
Условие
Составить схему алгоритма и программу, который имеет ГМ и ПП сортировки масива А=[ai]n без уменьшения (a1 ≤ a2 ≤ … ≤ ai ≤ … ≤ an) методом выбора.
Таблица символических имен
Имя |
Значения |
Тип |
Данные |
i |
индекс строки |
Целый |
Вычисляется |
n |
размер вектора |
Целый |
Задается |
j |
счетчик цикла |
Целый |
Вычисляется |
A |
вектор |
Действительный масив |
Задается |
M |
запоминающая переменная |
Действительный |
Вычисляется |
Блок схема
Obr
A
B
j<= 1, n-1, 1
A[i+1]<=M
Конец i
i<= 1, n-1, 1
A[i]>A[i+1]
Конец i
Нет
M<=A[i]
Да
Obr
A[i]<=A[i+1]
A
B
Начало
ввод
n, А
вывод
А
Obr
А
вывод
Конец
Программа сортировки массива
#include<iostream.h>
#include<conio.h>
#include<stdio.h>
void Obr(float A[10], int n)
{
int i, j;
float M;
for(j=0;j<n-1;j++)
for(i=0;i<n-1;i++)
{
if(A[i]>A[i+1])
{
M=A[i];
A[i]=A[i+1];
A[i+1]=M;
}
}
}
void main()
{
int n, i;
float A[10];
clrscr();
cout<<"Vvedite n=";
cin>>n;
cout<<"Vvedite vektor\n";
for(i=0;i<n;i++)
{
cout<<"A["<<i+1<<"]=";
cin>>A[i];
}
clrscr();
cout<<"Ishodnuy vektor\n";
for(i=0;i<n;i++)
cout<<A[i]<<"\t";
Obr(A, n);
cout<<"\n\nOtsortirovanuy vektor\n";
for(i=0;i<n;i++)
cout<<A[i]<<"\t";
}
Результат сортировки
Ishodnuy vector
5 -1 7 -3 0 4 -2 6
Otsortirovanuy vector
-3 -2 -1 0 4 5 6 7
Задание 6. Операции с файлами
Условие
Дан файл F, компоненты которого целые числа. Найти:
а) большее значение среди компонентов;
б) меньшее значение среди компонентов с четными индексами;
в) большее значение среди модулей компонентов с нечетными индексами;
г) сумму большего и меньшего значений компонентов;
д) разницу первого и последнего компонентов файла.
Таблица символических имен
Имя |
Значения |
Тип |
Данные |
i |
индекс элемента |
Целый |
Вычисляется |
n |
размер вектора |
Целый |
Задается |
A |
вектор |
Действительный масив |
Задается |
f1 |
текстовый документ |
файл |
Задается |
max |
больший элемент |
Целый |
Вычисляется |
min |
меньший элемент |
Целый |
Вычисляется |
minp |
меньший элемент компонентов с четными индексами |
Целый |
Вычисляется |
maxmn |
больший по модулю элемент компонентов с нечетными индексами |
Целый |
Вычисляется |
r |
разность первого и последнего компонента |
Целый |
Вычисляется |
s |
сумма большего и меньшего элемента |
Целый |
Вычисляется |
начало
f1=fopen
(“F.txt”,”r”)
ввод
А
max<=A[1]
min<=A[1]
maxmn<=A[1]
minp<=A[2]
i<= 1, n, 1
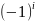
Да
Нет
|maxmn|<
|A[i]|
Да
Нет
minp>A[i]
Да
Нет
А
B
C
D
А
B
C
D
maxmn<=A[1]
minp<=A[2]
max<A[i]
Да
Нет
max<=A[1]
min>A[i]
Да
Нет
min<=A[1]
F
F
конец i
r<=A[1]-A[n]
s<=max+min
max, minp, maxmn, s,r
вывод
конец