9. (23) Распределение зарядов в проводнике.

Мы видели, что поверхность проводника, как нейтрального, так и заряженного, является эквипотенциальной поверхностью (§ 24) и внутри проводника напряженность поля равна нулю (§ 16). То же относится и к полому проводнику: поверхность его есть поверхность эквипотенциальная и поле внутри полости равно нулю, как бы сильно ни был заряжен проводник, если, конечно, внутри полости нет изолированных от проводника заряженных тел.

Этот вывод был наглядно продемонстрирован английским физиком Майклом Фарадеем (1791—1861), обогатившим науку рядом крупнейших открытий. Его опыт состоял в следующем. Большая деревянная клетка была оклеена листами станиоля (оловянной бумагой), изолирована от Земли и сильно заряжена при помощи электрической машины. В клетку помещался сам Фарадей с очень чувствительным электроскопом. Несмотря на то, что с внешней поверхности клетки при приближении к ней тел, соединенных с Землей, вылетали искры, указывая этим на большую разность потенциалов между клеткой и Землей, электроскоп внутри клетки не показывал никакого отклонения (рис. 53). Видоизменение этого опыта показано на рис. 54. Если сделать из металлической сетки замкнутую полость и привесить листочки бумаги с внутренней и внешней сторон полости, то обнаружим, что отклоняются лишь наружные

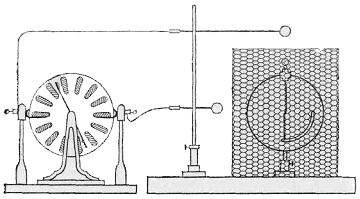
Рис. 53. Опыт Фарадея

Рис. 54. Видоизменение опыта Фарадея. Металлическая клетка заряжена. Листочки бумаги снаружи отклоняются, указывая на наличие заряда на внешних поверхностях стен клетки. Внутри клетки заряда нет, листочки бумаги не отклоняются

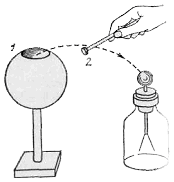
Рис. 55. Исследование распределения заряда в проводнике 1 при помощи пробной пластинки 2. Внутри полости проводника заряда нет

листочки. Это показывает, что электрическое поле существует только в пространстве между клеткой и окружающими ее предметами, т. е. снаружи клетки; внутри же клетки поле отсутствует. При зарядке любого проводника заряды распределяются в нем так, что электрическое поле внутри него исчезает и разность потенциалов между любыми точками обращается в нуль. Посмотрим, каким образом для этого должны разместиться заряды.

Зарядим полый проводник, например полый изолированный шар 1 (рис. 55), имеющий небольшое отверстие. Возьмем маленькую металлическую пластинку 2 укрепленную на изолирующей ручке («пробную пластинку») коснемся ею какого-либо места внешней поверхности шара и затем приведем в соприкосновение с электроскопом. Листки электроскопа разойдутся на некоторый угол, указывая этим, что пробная пластинка при соприкосновении с шаром зарядилась. Если мы, однако, коснемся пробной пластинкой внутренней поверхности шара, то пластинка будет оставаться незаряженной, как бы сильно ни был заряжен шар Почерпнуть заряды можно только с внешней поверхности проводника, а с внутренней это оказывается невозможным. Более того, если мы предварительно зарядим пробную пластинку и коснемся ею внутренней поверхности проводника, то весь заряд перейдет на этот проводник. Это происходит независимо от того, какой заряд уже имелся на проводнике. В § 19 мы подробно разъяснили это явление. Итак, в состоянии равновесия заряды распределяются только на внешней поверхности проводника. Конечно, если бы мы повторили с полым проводником опыт, изображенный на рис. 45, касаясь проводника концом проволоки, ведущей к электрометру, то убедились бы, что вся поверхность проводника, как внешняя, так и внутренняя, есть поверхность одного потенциала: распределение зарядов по внешней поверхности проводника есть результат действия электрического поля. Только тогда, когда весь заряд перейдет на поверхность проводника, установится равновесие, т. е. внутри проводника напряженность поля сделается равной нулю и все точки проводника (внешняя поверхность, внутренняя поверхность и точки в толще металла) будут иметь один и тот же потенциал.

Таким образом, проводящая поверхность вполне защищает область, которую она окружает, от действия электрического поля, созданного зарядами, расположенными на этой поверхности или вне ее. Линии внешнего поля оканчиваются на этой поверхности, в проводящем слое они не могут проходить, и внутренняя полость оказывается свободной от поля. Поэтому такие металлические поверхности называются электростатическими защитами. Интересно отметить, что даже поверхность, сделанная из металлической сетки, может служить защитой, если только сетка достаточно густа.

31.1. В центре полого изолированного металлического шара находится заряд. Отклонится ли заряженный грузик, подвешенный на шелковой нити и помещенный вне шара? Разберите подробно, что при этом происходит. Что будет, если шар заземлен?

31.2. Почему пороховые склады для защиты от удара молний окружают со всех сторон заземленной металлической сеткой? Почему введенные в такое здание водопроводные трубы должны быть также хорошо заземлены?

Тем обстоятельством, что заряды распределяются на внешней поверхности проводника, часто пользуются на практике. Когда желают полностью перенести заряд какого-нибудь проводника на электроскоп (или электрометр), то к электроскопу присоединяют по возможности замкнутую металлическую полость и вводят заряженный проводник внутрь этой полости. Проводник полностью разряжается, и весь его заряд переходит на электроскоп. Это приспособление в честь Фарадея называют «фарадеевым цилиндром», так как на практике эта полость чаще всего выполняется в виде металлического цилиндра. Мы уже пользовались этим свойством фарадеева цилиндра (стакана) в опыте, изображенном на рис. 9, и подробно разъяснили его в § 19.

Ван-де-Грааф предложил использовать свойства фарадеева цилиндра для получения очень высоких напряжений. Принцип действия его генератора показан на рис. 56. Бесконечная лента 1 из какого-нибудь изолирующего материала, например шелка, движется при помощи мотора на двух роликах и одним своим концом заходит внутрь полого, изолированного от Земли металлического шара 2. Вне шара лента при помощи кисточки 3 заряжается каким-либо источником, например батареей или электрической машиной 4, до напряжения 30—50 кВ относительно Земли, если второй полюс батареи или машины заземлен. Внутри шара 2 заряженные участки ленты касаются кисточки 5 и полностью отдают шару свой заряд, который сейчас же перераспределяется по внешней поверхности шара. Благодаря этому ничто не препятствует непрерывному переносу заряда на шар. Напряжение между шаром 2 и Землей непрерывно увеличивается. Таким образом можно получить напряжение в несколько миллионов вольт. Подобные машины применяли в опытах по расщеплению атомных ядер.

Рис. 56. Принцип устройства генератора Ван-де-Граафа

Для того чтобы ответить на вопрос о распределении заряда в проводнике, нам надо уточнить некоторые свойства силовых линий электростатического поля. Напомним, что силовая линия электрического поля (в том числе и электростатического) — это воображаемая линия в пространстве, проведенная так, чтобы касательная к ней в каждой точке совпадала с вектором напряженности электрического поля в этой точке. Опыт изучения электростатических полей дает основание заключить, что силовые линии этих полей непрерывны и не замкнуты, они могут начинаться только на положительных зарядах и оканчиваться только на отрицательных и не могут начинаться (заканчиваться) в точке пространства, где нет зарядов. При графическом изображении поля некоторой системы зарядов число силовых линий, начинающихся или заканчивающихся на каком-либо заряде, пропорционально модулю этого заряда. Отсюда следует, что из любого заряда обязательно выходят (или входят в него) силовые линии.

После сказанного о силовых линиях возвратимся к вопросу о распределении заряда в проводнике. Выделим мысленно произвольный достаточно малый объем ΔV внутри проводника (рис. 1). Предположим, что этот объем имеет заряд (для определенности, положительный). Тогда из выделенного объема будут выходить силовые линии, т. е. вблизи него будет существовать электрическое поле. Но поля внутри проводника нет. Поэтому выделенный объем должен быть нейтрален. А поскольку этот объем взят нами в произвольном месте внутри проводника, то можно утверждать, что вся «внутренность» проводника нейтральна и, следовательно, весь заряд проводника находится на его поверхности.

Если поместить проводник во внешнее электростатическое поле или его зарядить, то на заряды проводника будет действовать электростатическое поле, в результате чего они начнут перемещаться. Перемещение зарядов (ток) продолжается до тех пор, пока не установится равновесное распределение зарядов, при котором электростатическое поле внутри проводника обращается в нуль. Это происходит в течение очень короткого времени. В самом деле, если бы поле не было равно нулю, то в проводнике возникло бы упорядоченное движение зарядов без затраты энергии от внешнего источника, что противоречит закону сохранения энергии. Итак, напряженность поля во всех точках внутри проводника равна нулю:

Отсутствие поля внутри проводника означает, согласно (85.2), что потенциал во всех точках внутри проводника постоянен ( = const), т. е. поверхность проводника в электростатическом поле является эквипотенциальной (см. § 85). Отсюда же следует, что вектор напряженности поля на внешней поверхности проводника направлен по нормали к каждой точке его поверхности. Если бы это было не так, то под действием касательной составляющей Е заряды начали бы по поверхности проводника переме­щаться, что, в свою очередь, противоречило бы равновесному распределению зарядов.

Если проводнику сообщить некоторый заряд Q, то нескомпенсированные заряды располагаются только на поверхности проводника. Это следует непосредственно из теоремы Гаусса (89.3), согласно которой заряд Q, находящийся внутри проводника в некотором объеме, ограниченном произвольной замкнутой поверхностью, равен

так как во всех точках внутри поверхности D=0.

Найдем взаимосвязь между напряженностью Е поля вблизи поверхности заряжен­ного проводника и поверхностной плотностью  зарядов на его поверхности. Для этого применим теорему Гаусса к бесконечно малому цилиндру с основаниями S, пересека­ющему границу проводник — диэлектрик. Ось цилиндра ориентирована вдоль вектора Е (рис. 141). Поток вектора электрического смещения через внутреннюю часть цилинд­рической поверхности равен нулю, так как внутри проводника Е₁ (а следовательно, и D₁) равен нулю, поэтому поток вектора D сквозь замкнутую цилиндрическую поверхность определяется только потоком сквозь наружное основание цилиндра. Со­гласно теореме Гаусса (89.3), этот поток (DS) равен сумме зарядов (Q=S), охваты­ваемых поверхностью: DS=S т.е.

(92.1)

или

(92.2)

где  — диэлектрическая проницаемость среды, окружающей проводник.

Таким образом, напряженность электростатического поля у поверхности провод­ника определяется поверхностной плотностью зарядов. Можно показать, что соот­ношение (92.2) задает напряженность электростатического поля вблизи поверхности проводника любой формы.

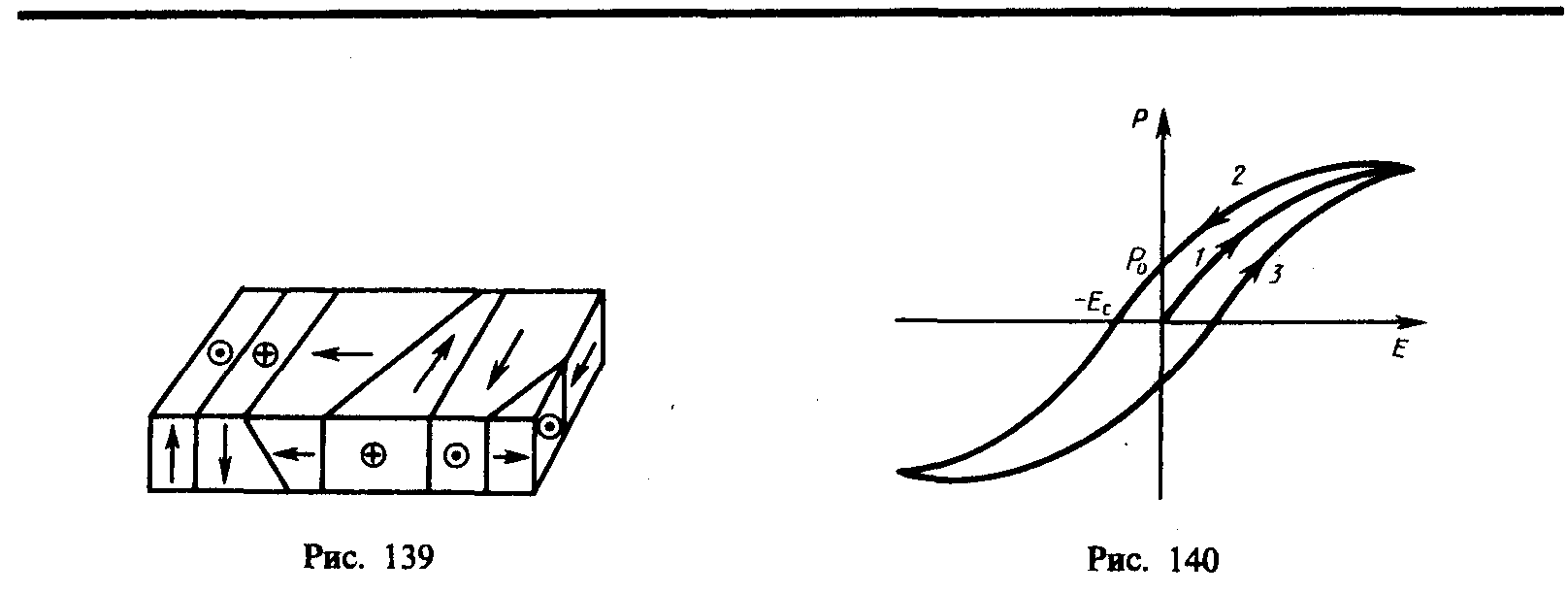
Если во внешнее электростатическое поле внести нейтральный проводник, то свободные заряды (электроны, ионы) будут перемещаться: положительные — по полю, отрицательные — против поля (рис. 142, а). На одном конце проводника будет скап­ливаться избыток положительного заряда, на другом — избыток отрицательного. Эти заряды называются индуцированными. Процесс будет происходить до тех пор, пока напряженность поля внутри проводника не станет равной нулю, а линии напряжен­ности вне проводника — перпендикулярными его поверхности (рис. 142, б). Таким образом, нейтральный проводник, внесенный в электростатическое поле, разрывает часть линий напряженности; они заканчиваются на отрицательных индуцированных зарядах и вновь начинаются на положительных. Индуцированные заряды распределяются на внешней поверхности проводника. Явление перераспределения поверхностных зарядов на проводнике во внешнем электростатическом поле называется электростати­ческой индукцией.

Из рис. 142, б следует, что индуцированные заряды появляются на проводнике вследствие смещения их под действием поля, т. е.  является поверхностной плот­ностью смещенных зарядов. По (92.1), электрическое смещение D вблизи проводника численно равно поверхностной плотности смещенных зарядов. Поэтому вектор D по­лучил название вектора электрического смещения.

Так как в состоянии равновесия внутри проводника заряды отсутствуют, то созда­ние внутри него полости не повлияет на конфигурацию расположения зарядов и тем самым на электростатическое поле. Следовательно, внутри полости поле будет отсут­ствовать. Если теперь этот проводник с полостью заземлить, то потенциал во всех точках полости будет нулевым, т. е. полость полностью изолирована от влияния внешних электростатических полей. На этом основана электростатическая защи­та — экранирование тел, например измерительных приборов, от влияния внешних электростатических полей. Вместо сплошного проводника для защиты может быть использована густая металлическая сетка, которая, кстати, является эффективной при наличии не только постоянных, но и переменных электрических полей.

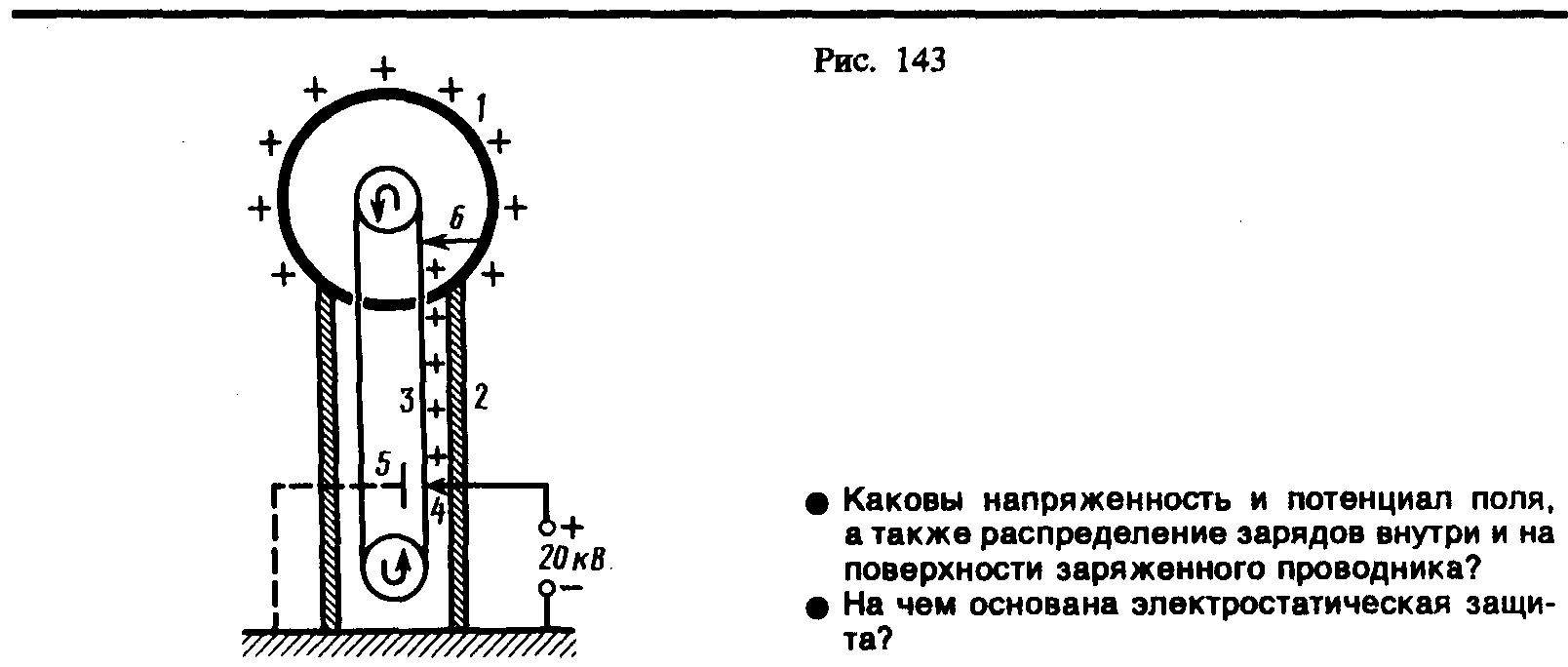
Свойство зарядов располагаться на внешней поверхности проводника используется для устройства электростатических генераторов, предназначенных для накопления бо­льших зарядов и достижения разности потенциалов в несколько миллионов вольт. Электростатический генератор, изобретенный американским физиком Р. Ван-де-Граафом (1901—1967), состоит из шарообразного полого проводника 1 (рис. 143), укре­пленного на изоляторах 2. Движущаяся замкнутая лента 3 из прорезиненной ткани заряжается от источника напряжения с помощью системы остриев 4, соединенных с одним из полюсов источника, второй полюс которого заземлен. Заземленная пласти­на 5 усиливает стекание зарядов с остриев на ленту. Другая система остриев 6 снимает заряды с ленты и передает их полому шару, и они переходят на его внешнюю поверхность. Таким образом, сфере передается постепенно большой заряд и удается достичь разности потенциалов в несколько миллионов вольт. Электростатические генераторы применяются в высоковольтных ускорителях заряженных частиц, а также в слаботочной высоковольтной технике.