Каноническая форма задач линейного программирования
В каждой задаче ЛП ищутся значения переменных при условии, чтобы:
эти значения удовлетворяли некоторой системе линейных уравнений или неравенств;
при этих значениях целевая функция обращалась бы в минимум или максимум.
Одним из универсальных методов ЛП является симплексный метод, который, однако, можно применять, если задача ЛП имеет каноническую форму.
Определение. Задача ЛП имеет каноническую форму, если все ограничения системы состоят только из уравнений (кроме неравенств, выражающих неотрицательность переменных) и целевую функцию необходимо минимизировать. Примером такой задачи ЛП в канонической форме является задача 1 – сбалансированная транспортная задача с системой ограничений (1) и целевой функцией (2). Однако в большинстве экономических задач чаще всего в систему ограничений первоначально входят не только уравнения, а и неравенства.
Утверждение. Любая общая задача ЛП может быть приведена к канонической форме. Приведение общей задачи ЛП к канонической форме достигается путем введения новых (их называют дополнительными) переменных. Система ограничений (3) этой задачи состоит из четырех неравенств. Введя дополнительные переменныеy1 ≥ 0, y2 ≥ 0,y3 ≥ 0, y4 ≥ 0, можно перейти к системе ограничений:
Эти дополнительные переменные y i имеют абсолютно ясный экономический смысл, а именно означают величину неиспользованного времени работы (простоя машины i-го вида). Например, если бы машины первого вида работали все 18 ч, то x + y = 18, следовательно, y1 = 0. Но мы допускаем возможность неполного использования времени работы первой машины x + y<18. В этом случае y1 приобретает положительное значение и может рассматриваться как неиспользованный лимит времени. Например, зная решение этой задачи из пункта 3.3.2, x = 12, y = 6, мы можем из системы ограничений (3.9) сделать вывод, что y1 = y2 = y3 = 0, а y4 = 12 – 6 = 6. Т. е. машины первого, второго, третьего вида используют свое рабочее время полностью. А вот четвертая машина загружена лишь наполовину, 6 часов, и при заданном оптимальном плане простаивает. Возможно, после таких выводов руководителю предприятия захочется загрузить ее другой работой, сдать в аренду на это время и т.д. Итак, введением дополнительных переменных мы можем любое ограничение типа неравенства привести к уравнению.
Рассмотрим задачу о смеси. Система ограничений имеет вид:
Неравенства были обращены в сторону «больше», поэтому вводя дополнительные переменные y1, y2, y3 ≥ 0, их необходимо вычесть из левой части, чтобы уравнять ее с правой. Получим систему ограничений в канонической форме:
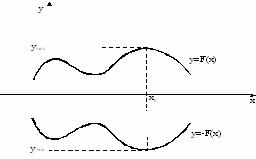
Переменные yi также будут иметь экономический смысл. Если вы вспомните практическое содержание задачи, то переменная y1 будет означать количество излишнего вещества А в смеси, y2 –количество излишков вещества В в смеси, y3– излишки С в смеси. Задача нахождения максимального значения целевой функции может быть сведена к нахождению минимума для функции –F ввиду очевидности утверждения maxF = –min (–F ). Посмотрите на рисунок 3.9: если в какой-то точке x= x0 функция y=F(x) достигает своего максимума, то функция y= –F(x), симметричная ей относительно оси OX, в этой же точке x0достигнет минимума, причем Fmax = – (–Fmin) при x = x0.
Вывод. Для представления задачи ЛП в канонической форме необходимо:
неравенства, входящие в систему ограничений задачи, преобразовать в уравнения с помощью введения дополнительных переменных;
если целевая функция F →max (максимизируется), она заменяется на функцию –F→ min (которая минимизируется).
Графический метод решения задачи линейного программирования
Если число переменных в задаче линейного программирования (ЗЛП) равно двум, а ограничениями является система неравенств, то задачу можно решать графическим методом.
Пример 3.1
При продаже двух видов товара используется 4 типа ресурсов. Норма затрат ресурсов на реализацию единицы товара, общий объем каждого ресурса заданы в табл. 3.2.
Прибыль от реализации одной единицы товара первого вида составляет 2 усл. ед., второго вида – 3 усл. ед.
Требуется найти оптимальный план реализации товаров, обеспечивающий торговому предприятию максимальную прибыль.
Таблица 3.2
Ресурсы |
Норма затрат ресурсов на товары |
Общее количество ресурсов |
||
|
1 -го вида |
2-го вида |
|
|
1 2 3 4 |
2 1 4 0 |
2 2 0 4 |
12 8 16 12 |
|
Решение
Это задача составления плана реализации товара при n=2, m=4.
Математическая модель имеет вид
(3.16)
В модели управляющие переменные х1,х2 – количество реализуемых изделий первого и второго вида, соответственно, Р – прибыль. Система неравенств включает ограничения по ресурсам. Количество ресурсов на реализацию товаров первого и второго вида не превышает общего количества ресурсов каждого типа.
Графическое решение.
Построим в плоскости X1OX2 область допустимых решений. Каждое неравенство системы (3.3.2) определяет в плоскости X1OX2 полуплоскость, лежащую выше или ниже прямой, определяемой соответствующим уравнением. Построим прямые (см. рис. 3.1)
Рассмотрим точку с координатами х1 =0; х2 =0. Подставив их в первое неравенство, получаем 0 12 – верно, следовательно, искомая полуплоскость лежит ниже прямой 2x1 +2x2 = 12; остальные полуплоскости находятся аналогичным образом.
Область OABCD – область допустимых решений задачи.
Для нахождения максимального значения Р проверим граничные. Точки из области решений.
Построим две линии уровня (рис. 3.1):
2x1 + 3x2 = 6;
2x1 +3х2=13.
Функция Р возрастает
в направлении вектора-нормали 
=
(2,3) следовательно, минимум находится в
точке (0.0). Максимум определяем, передвигая
нашу линию уровня в направлении
вектора
параллельно
самой себе до тех пор, пока хотя бы одна
ее точка будет принадлежать области
допустимых решений.
В данном случае это точка: х1 = 4, х2 = 2;
при этом P=2*4+3*2=14.
Таким образом, для получения максимальной прибыли в размере 14 усл. ед. надо продать 4 изделия первого вида и 2 изделия второго вида.
Рис. 3.1. Графический метод решения задачи ЛП
Изложенный выше графический метод применим для решения задач линейного программирования следующего вида:
(3.17)
(3.18)
Алгоритм решения ЗЛП графическим методом.
1) Записывают уравнения прямых, соответствующих ограничениям (3.3.4), и строят их на плоскости x1ox3.
2) Определяют области, в которых выполняются ограничения задачи. Для этого выбирают произвольную точку на плоскости х1ох2 и подставляют ее координаты в первую часть одного из неравенств. Если неравенство верно, то искомая полуплоскость находится с той же стороны от прямой, что и точка; в противном случае искомая полуплоскость лежит с противоположной стороны от прямой. Эти действия последовательно выполняются для всех неравенств (3.3.4).
3) Определяют область допустимых решений задачи как область пересечения т полуплоскостей, соответствующих т ограничениям задачи.
4) Определяют
направление возрастания (убывания)
целевой функции f. Это можно
сделать двумя способами. Можно построить
вектор-нормаль 
,
его направление показывает направление
возрастания функции f,
и противоположном направлении функция
убывает. Можно просто построить две
линии уровня функции f = K1; f = K2;
(K1, K2 –
произвольные константы, K1 
K2),
и по их расположению определить
направление возрастания (убывания)
функции.
5) Определяют граничную точку (точки) области допустимых решений, в которых целевая функция принимает максимальное или минимальное значение.
6) Вычисляют значения найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.
Возможны следующие варианты областей допустимых решений (рис. 3.2):
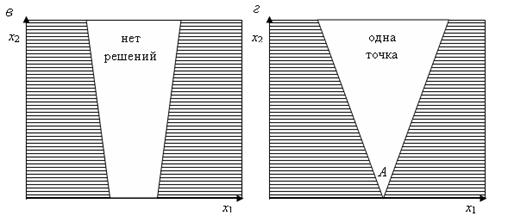
Рис. 3.2. Варианты областей. а – область допустимых решений – замкнутое множество (многоугольник); б – область допустимых решений – открытое множество; в – область допустимых решений – пустое множество (система ограничений (3.18) несовместна); г – область допустимых решений состоит из единственной точки А
На рис. 3.2 показаны варианты пересечения линии уровня целевой функции с областью допустимых решений. Может быть единственное решение – точка В, бесконечно много решений – отрезок CD (рис. 3.2, а), максимальным (минимальным) значением целевой функции может быть бесконечность (рис. 3.2, б). Область ограничений несовместимо (допустимых решений нет, рис. 3.2, в). И может быть только одна допустимая точка (рис. 3.2, г)
Алгоритм решения ЗЛП графическим методом.
1) Записывают уравнения прямых, соответствующих ограничениям (3.3.4), и строят их на плоскости x1ox3.
2) Определяют области, в которых выполняются ограничения задачи. Для этого выбирают произвольную точку на плоскости х1ох2 и подставляют ее координаты в первую часть одного из неравенств. Если неравенство верно, то искомая полуплоскость находится с той же стороны от прямой, что и точка; в противном случае искомая полуплоскость лежит с противоположной стороны от прямой. Эти действия последовательно выполняются для всех неравенств (3.3.4).
3) Определяют область допустимых решений задачи как область пересечения т полуплоскостей, соответствующих т ограничениям задачи.
4) Определяют направление возрастания (убывания) целевой функции f. Это можно сделать двумя способами. Можно построить вектор-нормаль , его направление показывает направление возрастания функции f, и противоположном направлении функция убывает. Можно просто построить две линии уровня функции f = K1; f = K2; (K1, K2 – произвольные константы, K1 K2), и по их расположению определить направление возрастания (убывания) функции.
5) Определяют граничную точку (точки) области допустимых решений, в которых целевая функция принимает максимальное или минимальное значение.
6) Вычисляют значения найденной точки, решая совместно уравнения, задающие прямые, на пересечении которых находится эта точка, или выявляя уравнение граничной прямой области допустимых решений, с которой совпадает линия уровня целевой функции.
Возможны следующие варианты областей допустимых решений (рис. 3.2):
Рис. 3.2. Варианты областей. а – область допустимых решений – замкнутое множество (многоугольник); б – область допустимых решений – открытое множество; в – область допустимых решений – пустое множество (система ограничений (3.18) несовместна); г – область допустимых решений состоит из единственной точки А
На рис. 3.2 показаны варианты пересечения линии уровня целевой функции с областью допустимых решений. Может быть единственное решение – точка В, бесконечно много решений – отрезок CD (рис. 3.2, а), максимальным (минимальным) значением целевой функции может быть бесконечность (рис. 3.2, б). Область ограничений несовместимо (допустимых решений нет, рис. 3.2, в). И может быть только одна допустимая точка (рис. 3.2, г)
Симплексный метод решения задач линейного программирования
СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (симплекс-метод) [simplex method] — вычислительная процедура, основанная на принципе последовательного улучшения решений — перехода от одной базисной точки (см. Базисное решение) к другой, для которой значениецелевой функции больше (эти операции фиксируются в симплексной таблице). Доказано, что еслиоптимальное решение существует, то оно обязательно будет найдено через конечное число шагов (за исключением т. н. вырожденной задачи, при которой возможно явление “зацикливания”, т. е. многократного возврата к одному и тому же положению). Название метод получил от термина “n-мерныйсимплекс”. Геометрическая интерпретация метода состоит в последовательном движении по вершинамсимплекса.
Задача линейного программирования состоит в том, что необходимо максимизировать или минимизировать некоторый линейный функционал на многомерном пространстве при заданных линейных ограничениях.
Заметим, что каждое из линейных неравенств на переменные ограничивает полупространство в соответствующем линейном пространстве. В результате все неравенства ограничивают некоторый многогранник (возможно, бесконечный), называемый также полиэдральным комплексом. Уравнение W(x) = c, где W(x) — максимизируемый (или минимизируемый) линейный функционал, порождает гиперплоскость L(c). Зависимость от cпорождает семейство параллельных гиперплоскостей. Тогда экстремальная задача приобретает следующую формулировку — требуется найти такое наибольшее c, что гиперплоскость L(c) пересекает многогранник хотя бы в одной точке. Заметим, что пересечение оптимальной гиперплоскости и многогранника будет содержать хотя бы одну вершину, причём, их будет более одной, если пересечение содержит ребро или k-мерную грань. Поэтому максимум функционала можно искать в вершинах многогранника. Принцип симплекс-метода состоит в том, что выбирается одна из вершин многогранника, после чего начинается движение по его рёбрам от вершины к вершине в сторону увеличения значения функционала. Когда переход по ребру из текущей вершины в другую вершину с более высоким значением функционала невозможен, считается, что оптимальное значение c найдено.
Последовательность вычислений симплекс-методом можно разделить на две основные фазы:
нахождение исходной вершины множества допустимых решений,
последовательный переход от одной вершины к другой, ведущий к оптимизации значения целевой функции.
При этом в некоторых случаях исходное решение очевидно или его определение не требует сложных вычислений, например, когда все ограничения представлены неравенствами вида «меньше или равно» (тогда нулевой вектор совершенно точно является допустимым решением, хотя и, скорее всего, далеко не самым оптимальным). В таких задачах первую фазу симплекс-метода можно вообще не проводить. Симплекс-метод, соответственно, делится на однофазный и двухфазный.
Теоретические основы симплексного метода