Платежная матрица. Нижняя и верхняя цена игры.

Оглавление | Назад | Далее| Глоссарий понятий

Рассмотрим парную конечную игру. Пусть игрок А располагает m личными стратегиями, которые обозначим A₁, A₂, ..., A_m. Пусть у игрока В имеется n личных стратегий, обозначим их B₁, B₂, ..., B_m. Говорят, что игра имеет размерность m × n. В результате выбора игроками любой пары стратегий

A_i и B_j (i = 1, 2, ..., m; j = 1, 2, ..., n)

однозначно определяется исход игры, т.е. выигрыш a_ij игрока А (положительный или отрицательный) и проигрыш (- a_ij ) игрока В. Предположим, что значения о,у известны для любой пары стратегий (A_i ,B_j ). Матрица P = (a_ij ), i = 1, 2, ..., m; j = 1, 2, ..., n, элементами которой являются выигрыши, соответствующие стратегиям A_i и B_j , называется платежной матрицей или матрицей игры. Общий вид такой матрицы представлен в таблице 3.1.

Таблица 3.1

Строки этой таблицы соответствуют стратегиям игрока А, а столбцы — стратегиям игрока В. Составим платежную матрицу для следующей игры.

Седлова точка

Седловая точка в математическом анализе — такая точка из области определения функции, которая является стационарной для данной функции, однако не является её локальным экстремумом. В такой точке, если рассматривается функция двух переменных, образованная графиком функцииповерхность обычно напоминает по форме седло или горный перевал — выпуклая в одном направлении и вогнутая в другом. На карте высот седловая точка может быть в общем случае обнаружена в месте пересечения изолиний. Например, два холма, между которыми находится высокий перевал, образуют седловую точку в вершине этого перевала: на карте высот это будет выглядеть как центр «восьмерки», образованной соответствующими изолиниями. Проверить, является ли данная стационарная точка функции F(x,y) двух переменных седловой, можно, вычислив матрицу Гессе функции в этой точке: если гессиан будет неопределенной квадратичной формой, то данная точка — седловая. Например, составив матрицу Гессе функции   в стационарной точке   получим матрицу:

которая является неопределенной. Поэтому, точка   данной функции — седловая. Однако вышеприведенный критерий предоставляет только достаточное условие наличия седловой точки. Например,   является седловой точкой функции  , но матрица Гессе в данном случае будет нулевой матрицей, которую, по определению, нельзя назвать неопределенной.

В общем случае, седловой точкой гладкой функции (график которой изображает кривую, поверхность или гиперповерхность) называется такая стационарная точка, в окрестностикоторой данная кривая/поверхность/гиперповерхность не лежит полностью по одну сторону касательного пространства в данной точке.

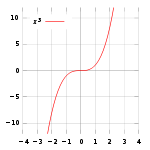
График y = x³ с седловой точкой в 0

В случае функции одной переменной, седловая точка — такая точка, которая одновременно является и стационарной точкой, и точкой перегиба (точка перегиба не является локальным экстремумом). !

Решение матричных игр в чистых стратегиях.

Матричная игра двух игроков с нулевой суммой может рассматриваться как следующая абстрактная игра двух игроков. Первый игрок имеет m стратегий i = 1,2,...,m, второй имеет n стратегий j = 1,2,...,n. Каждой паре стратегий (i,j) поставлено в соответствие число а_ij, выражающее выигрыш игрока 1 за счёт игрока 2, если первый игрок примет свою i-ю стратегию, а 2 – свою j-ю стратегию. Каждый из игроков делает один ход: игрок 1 выбирает свою i-ю стратегию (i= ), 2 – свою j-ю стратегию (j= ), после чего игрок 1 получает выигрыш а_ij за счёт игрока 2 (если а_ij< 0, то это значит, что игрок 1 платит второму сумму | а_ij | ). На этом игра заканчивается. Каждая стратегия игрока i= ; j =   часто называется чистой стратегией. Если рассмотреть матрицу А =  то проведение каждой партии матричной игры с матрицей ^ А сводится к выбору игроком 1 i-й строки, а игроком 2 j-го столбца и получения игроком 1 (за счёт игрока 2) выигрыша а_ij. Главным в исследовании игр является понятие оптимальных стратегий игроков. В это понятие интуитивно вкладывается такой смысл: стратегия игрока является оптимальной, если применение этой стратегии обеспечивает ему наибольший гарантированный выигрыш при всевозможных стратегиях другого игрока. Исходя из этих позиций, игрок 1 исследует матрицу выигрышей А следующим образом: для каждого значения i (i = ) определяется минимальное значение выигрыша в зависимости от применяемых стратегий игрока 2 а_ij (i =  ) т.е. определяется минимальный выигрыш для игрока 1 при условии, что он примет свою i-ю чистую стратегию, затем из этих минимальных выигрышей отыскивается такая стратегия i = i_о, при которой этот минимальный выигрыш будет максимальным, т.е. находится а_ij =  =   (1). Определение. Число  , определённое по формуле (1) называется нижней чистой ценой игры и показывает, какой минимальный выигрыш может гарантировать себе игрок 1, применяя свои чистые стратегии при всевозможных действиях игрока 2. Игрок 2 при оптимальном своём поведении должен стремится по возможности за счёт своих стратегий максимально уменьшить выигрыш игрока 1. Поэтому для игрока 2 отыскивается  а_ij т.е. определяется max выигрыш игрока 1, при условии, что игрок 2 применит свою j-ю чистую стратегию, затем игрок 2 отыскивает такую свою j = j₁стратегию, при которой игрок 1 получит min выигрыш, т.е. находит a_ij =  =   (2). Определение. Число  , определяемое по формуле (2), называется чистой верхней ценой игры и показывает, какой максимальный выигрыш за счёт своих стратегий может себе гарантировать игрок 1. Другими словами, применяя свои чистые стратегии игрок 1 может обеспечить себе выигрыш не меньше  , а игрок 2 за счёт применения своих чистых стратегий может не допустить выигрыш игрока 1 больше, чем  . Определение. Если в игре с матрицей А  = , то говорят, что эта игра имеет седловую точку в чистых стратегиях и чистую цену игры  =  = . Седловая точка – это пара чистых стратегий (i_о,j_о) соответственно игроков 1 и 2, при которых достигается равенство   =  . В это понятие вложен следующий смысл: если один из игроков придерживается стратегии, соответствующей седловой точке, то другой игрок не сможет поступить лучше, чем придерживаться стратегии, соответствующей седловой точке. Математически это можно записать и иначе:   где i, j – любые чистые стратегии соответственно игроков 1 и 2; (i_о,j_о) – стратегии, образующие седловую точку. Таким образом, исходя из (3), седловой элемент   является минимальным в i_о-й строке и максимальным в j_о-м столбце в матрице А. Отыскание седловой точки матрицы А происходит следующим образом: в матрице А последовательно в каждой строке находят минимальный элемент и проверяют, является ли этот элемент максимальным в своём столбце. Если да, то он и есть седловой элемент, а пара стратегий, ему соответствующая, образует седловую точку. Пара чистых стратегий (i_о,j_о) игроков 1 и 2, образующая седловую точку и седловой элемент  , называется решением игры. При этом i_о и j_о называютсяоптимальными чистыми стратегиями соответственно игроков 1 и 2.

Решение матричной игры в смешанных стратегиях.

Определение. Случайная величина, значениями которой являются чистые стратегии игрока, называется его смешанной стратегией. Таким образом, задание смешанной стратегии игрока состоит в указании тех вероятностей, с которыми выбираются его чистые стратегии. Будем обозначать смешанные стратегии игроков А и В соответственно S_A=||p₁, p₂, ..., p_m||, S_B=||q₁, q₂, ..., q_n||, где p_i - вероятность применения игроком А чистой стратегии А_і;  q_j - вероятность применения игроком В чистой стратегии B_j;  В часном случае, когда все вероятности, кроме одной, равны нулю, а эта одна - единице, смешанная стратегия превращается в чистую. Применение смешанных стратегий осуществляется, например, таким образом: игра повторяется много раз, но в каждом партии игрок применяет различные чистые стратегии, но с относительными частотами их применения, равными p_i и q_j. Смешанные стратегии в теории игр представляют собой модель изменчивой, гибкой тактики, когда ни один из игроков не знает, какую чистую стратегию выберет противник в данной партии. Если игрок А применяет смешанную стратегию S_A=||p₁, p₂, ..., p_m||, а игрок В смешанную стратегию S_B=||q₁, q₂, ..., q_n||, то средний выигрыш (математическое ожидание) игрока А определяется соотношением  (2.6.) Естественно, что ожидаемый проигрыш игрока В равен такой же величине. Итак, если матричная игра не имеет седловой точки, то игрок должен использовать оптимальную смешанную стратегию, которая обеспечит максимальный выигрыш . Естественно возникает вопрос: какими соображениями нужно руководствоватся при выборе смешанных стратегий? Оказывается принцип минимакса сохраняет свое значение и в этом случае. Кроме того важное значение для понимания решения игр, играют основные теоремы теории игр.

Графические методы решения игр

Графические методы решения игр. Следует отметить, что применение для решения задач (6.16)-(6.17), (6.18)-(6.19) стандартных алгоритмов линейного программирования далеко не всегда является рациональным. Помимо этого существуют иные методы, которые основываются на использовании специфики данных задач. В настоящем пункте мы остановимся на очень простом классическом способе поиска оптимальных смешанных стратегий в матричных играх, где один из участников имеет только две стратегии (это так называемые 2 х п и т х 2 игры).

Для определенности положим, что игрок I имеет возможность выбирать между двумя стратегиями с вероятностями x₁ и x₂ = 1-x₁, тогда его ожидаемые выигрыши, соответствующие чистым стратегиям игрока II, примут вид

или

т. е. ожидаемые выигрыши могут быть представлены в виде графиков линейных функций, зависящих от переменной x₁ ∊ [0; 1] (рис. 6.1, где предполагается, что игрок II имеет три стратегии).

Линии, изображенные на рис. 6.1, задают зависимости среднего выигрыша игрока I от значения вероятности x₁ , с которой он выбирает свою первую стратегию, для случаев, когда его противник выбирает первую, вторую или третью чистую стратегию. Тогда значениям минимального гарантированного дохода первого игрока соответствует нижняя огибающая всех трех прямых. Согласно принципу максимина, оптимальному выбору игрока I будет соответствовать наивысшая точка, лежащая на данной огибающей, отмеченная на рисунке как (x₁*, z*). Зная ее, можно определить оптимальную смешанную стратегию первого игрока х* = (x₁*, 1-x₂*) и цену игры, равную z*.

Исходя из отношения двойственности, которым, как было установлено в п. 6.1.5, связаны задачи обоих игроков, по оптимальной стратегии первого участника х* однозначно определяется оптимальная стратегия его противника у*. Поскольку у* является результатом решения задачи линейного программирования, то он обладает всеми свойствами допустимого базисного плана, т. е. в случае 2 х п игры имеет не более чем две ненулевых компоненты и не менее чем (п-2) нулевых. Номера ненулевых элементов у* определяются номерами линий, пересечение которых определило оптимальную стратегию первого игрока. Действительно, игрок II знает оптимальную стратегию соперника, и применение им стратегий, соответствующих прямым, проходящим выше точки (х₁*, z*), только увеличило бы его проигрыш.

В рассматриваемом примере это линии z₂ и z₃, и, следовательно, в своей оптимальной стратегии второй игрок должен с ненулевыми вероятностями применять вторую и третью чистые стратегии (у₂ >0, у₃ >0). На основе этого, а также учитывая условие нормировки

можем выразить: y₃ = l – y₂ тогда оптимальное значение y₂* может быть найдено из условия

или

В результате получаем оптимальную стратегию игрока II у*= (0, у₂*, у₃*).

Очевидно, что поиск решения в игре т х 2 осуществляется аналогичным образом с точностью до наоборот: строятся графики ожидаемого проигрыша игрока II, находится их верхняя огибающая и т. д.

Безусловно, графический способ в силу ограниченности круга задач, к которым он может быть применен, имеет скорее теоретическое, чем практическое значение. Однако он хорошо иллюстрирует содержательную сторону процесса поиска решения в игре.