6.2. Ханойские башни

Согласно легенде в Великом храме города Бенарас, под собором, отмечающим середину мира, находится бронзовый диск, на котором укреплены 3 алмазных стержня, высотой в один локоть и толщиной с пчелу. Давным-давно, в самом начале времен монахи этого монастыря провинились перед богом Брамой. Разгневанный, Брама воздвиг три высоких стержня и на один из них поместил 64 диска из чистого золота, причем так, что каждый меньший диск лежит на большем. Как только все 64 диска будут переложены со стержня, на который Бог Брама сложил их при создании мира, на другой стержень, башня вместе с храмом обратятся в пыль и под громовые раскаты погибнет мир. В процессе требуется, чтобы больший диск ни разу не оказывался над меньшим. Монахи в затруднении, в какой же последовательности стоит делать перекладывания? Требуется снабдить их софтом для расчета этой последовательности.

Независимо от Брамы данную головоломку в конце 19 века предложил французский математик Эдуард Люка. В продаваемом варианте обычно использовалось 7-8 дисков (рис. 7).

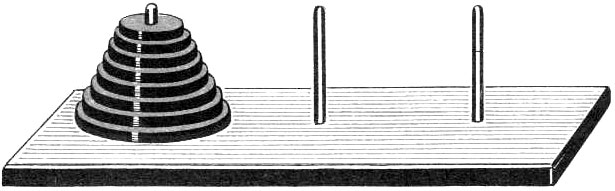
Рис. 7. Головоломка «Ханойские башни».

Предположим, что существует решение для n-1 диска. Тогда для перекладывания n дисков надо действовать следующим образом:

   1) Перекладываем n-1 диск.    2) Перекладываем n-й диск на оставшийся свободным штырь.    3) Перекладываем стопку из n-1 диска, полученную в пункте (1) поверх n-го диска.

Поскольку для случая n = 1 алгоритм перекладывания очевиден, то по индукции с помощью выполнения действий (1) – (3) можем переложить произвольное количество дисков.

Создадим рекурсивную процедуру, печатающую всю последовательность перекладываний для заданного количества дисков. Такая процедура при каждом своем вызове должна печатать информацию об одном перекладывании (из пункта 2 алгоритма). Для перекладываний из пунктов (1) и (3) процедура вызовет сама себя с уменьшенным на единицу количеством дисков.

1 2 3 4 5 6 7 8 9 10 11 12 13

//n – количество дисков //a, b, c – номера штырьков. Перекладывание производится со штырька a, //на штырек b при вспомогательном штырьке c. procedure Hanoi(n, a, b, c: integer); begin   if n > 1 then   begin     Hanoi(n-1, a, c, b);     writeln(a, ' -> ', b);     Hanoi(n-1, c, b, a);   end else     writeln(a, ' -> ', b);   end;

Заметим, что множество рекурсивно вызванных процедур в данном случае образует дерево, проходимое в обратном порядке.[15]

6.3. Синтаксический анализ арифметических выражений

Задача синтаксического анализа заключается в том, чтобы по имеющейся строке, содержащей арифметическое выражение, и известным значениям, входящих в нее переменных, вычислить значение выражения.

Процесс вычисления арифметических выражений можно представить в виде бинарного дерева. Действительно, каждый из арифметических операторов (+, –, *, /) требует двух операндов, которые также будут являться арифметическими выражениями и, соответственно могут рассматриваться как поддеревья. Рис. 8 показывает пример дерева, соответствующего выражению:

Рис. 8. Синтаксическое дерево, соответствующее арифметическому выражению (6).

В таком дереве концевыми узлами всегда будут переменные (здесь x) или числовые константы, а все внутренние узлы будут содержать арифметические операторы. Чтобы выполнить оператор, надо сначала вычислить его операнды. Таким образом, дерево на рисунке следует обходить в концевом порядке. Соответствующая последовательность узлов

называется обратной польской записью арифметического выражения.

При построении синтаксического дерева следует обратить внимание на следующую особенность. Если есть, например, выражение

и операции сложения и вычитания мы будем считывать слева на право, то правильное синтаксическое дерево будет содержать минус вместо плюса (рис. 9а). По сути, это дерево соответствует выражению   Облегчить составление дерева можно, если анализировать выражение (8) наоборот, справа налево. В этом случае получается дерево с рис. 9б, эквивалентное дереву 8а, но не требующее замены знаков.

Аналогично справа налево нужно анализировать выражения, содержащие операторы умножения и деления.[16]

Рис. 9. Синтаксические деревья для выражения a – b + c при чтении слева направо (а) и справа налево (б).