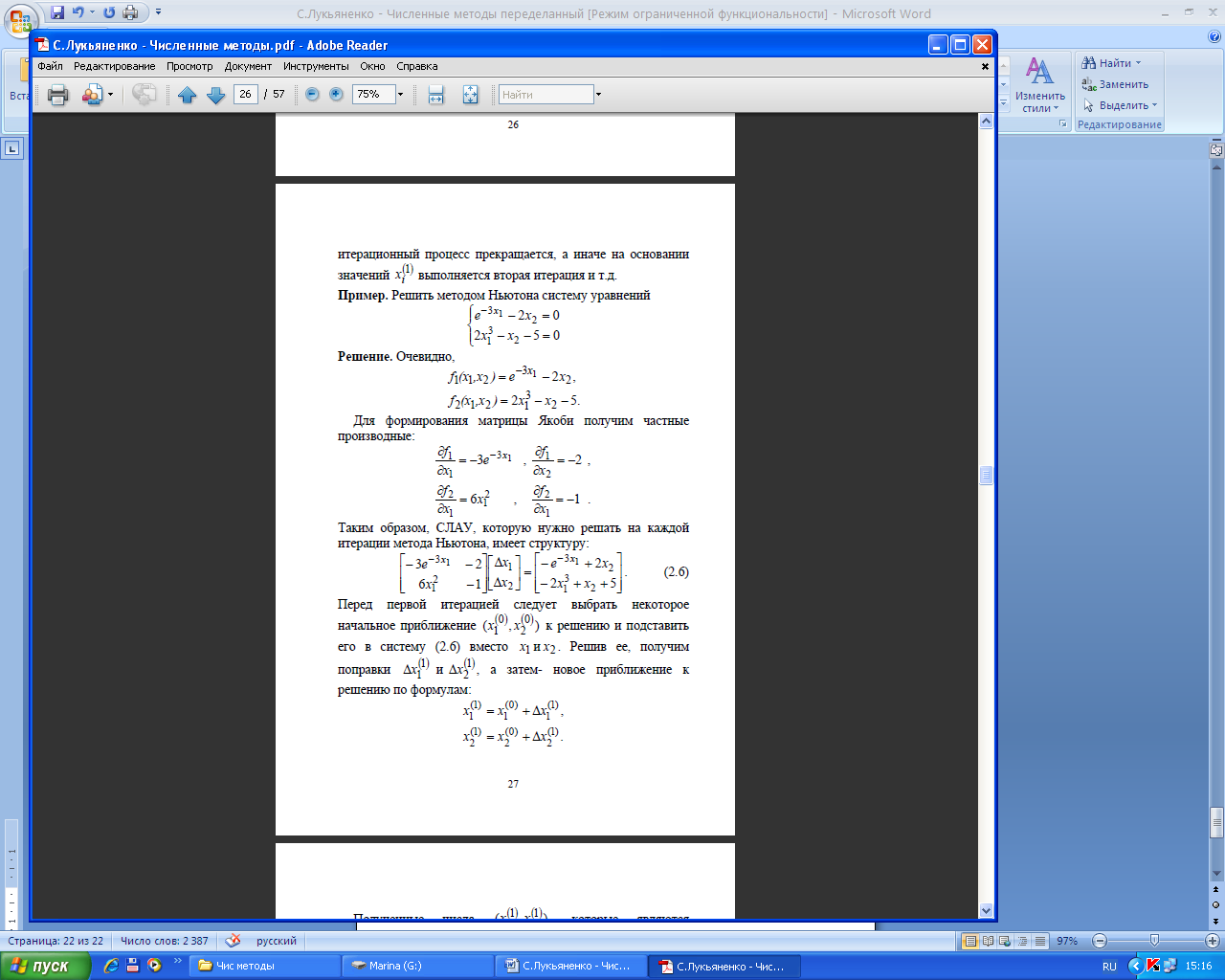
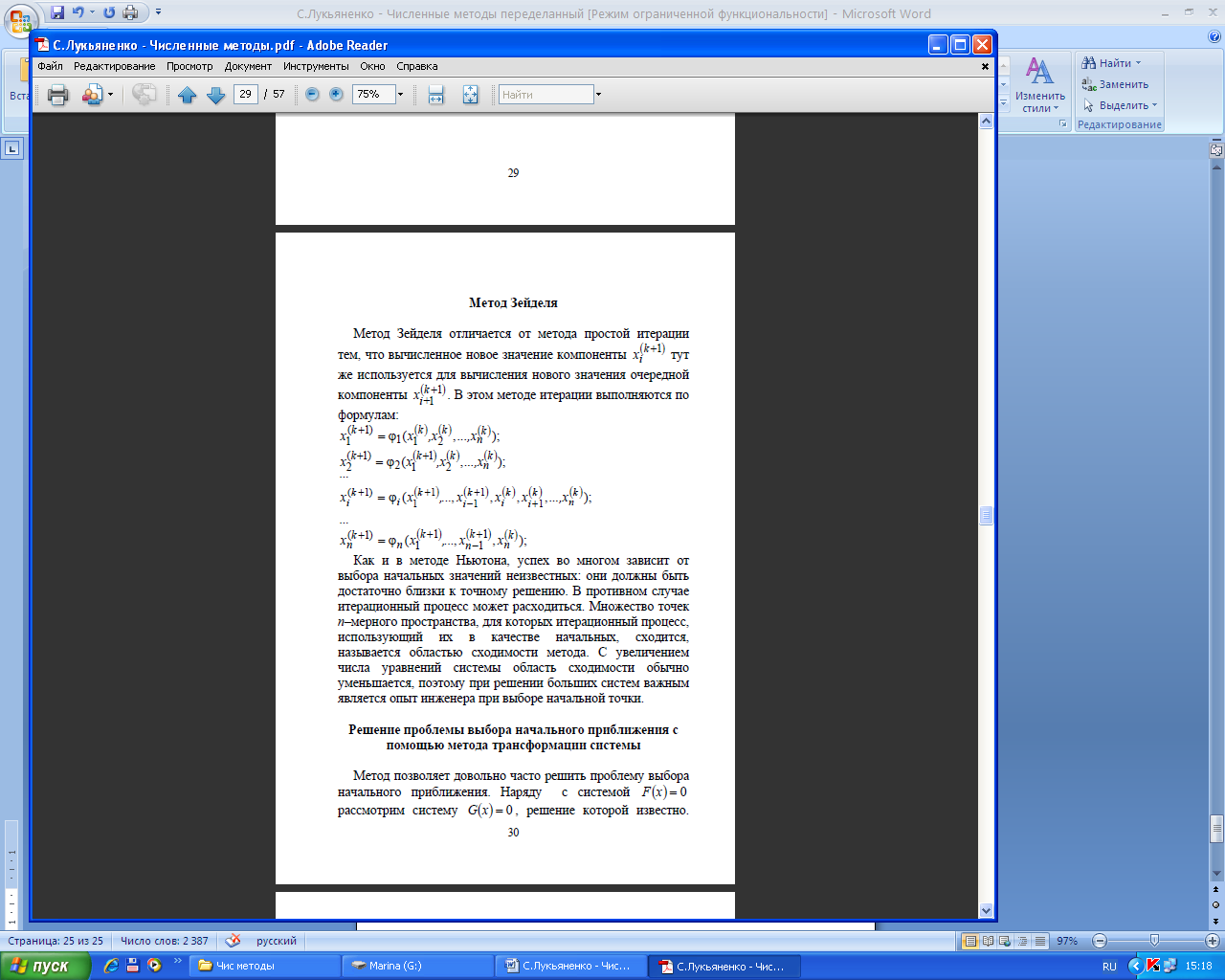
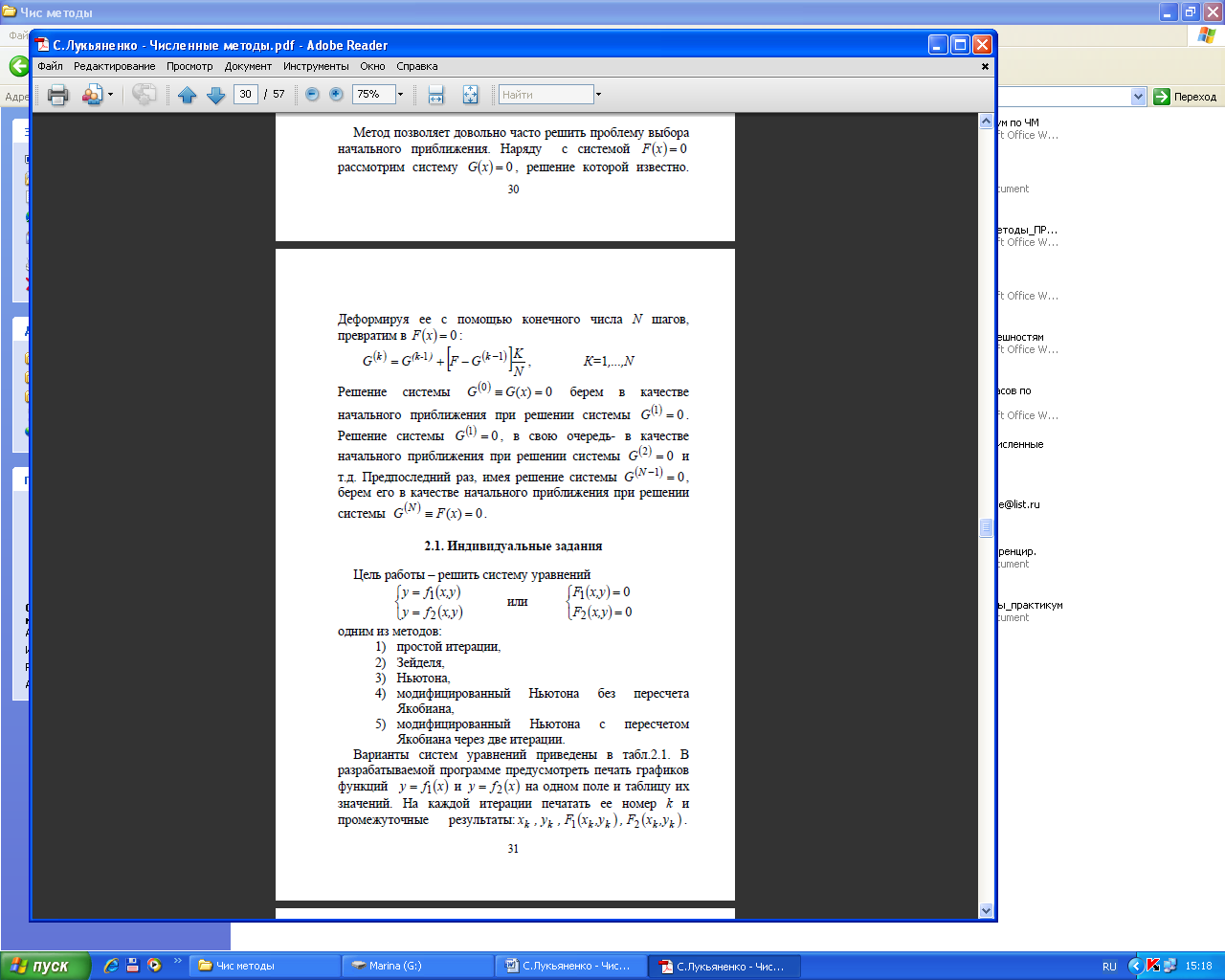
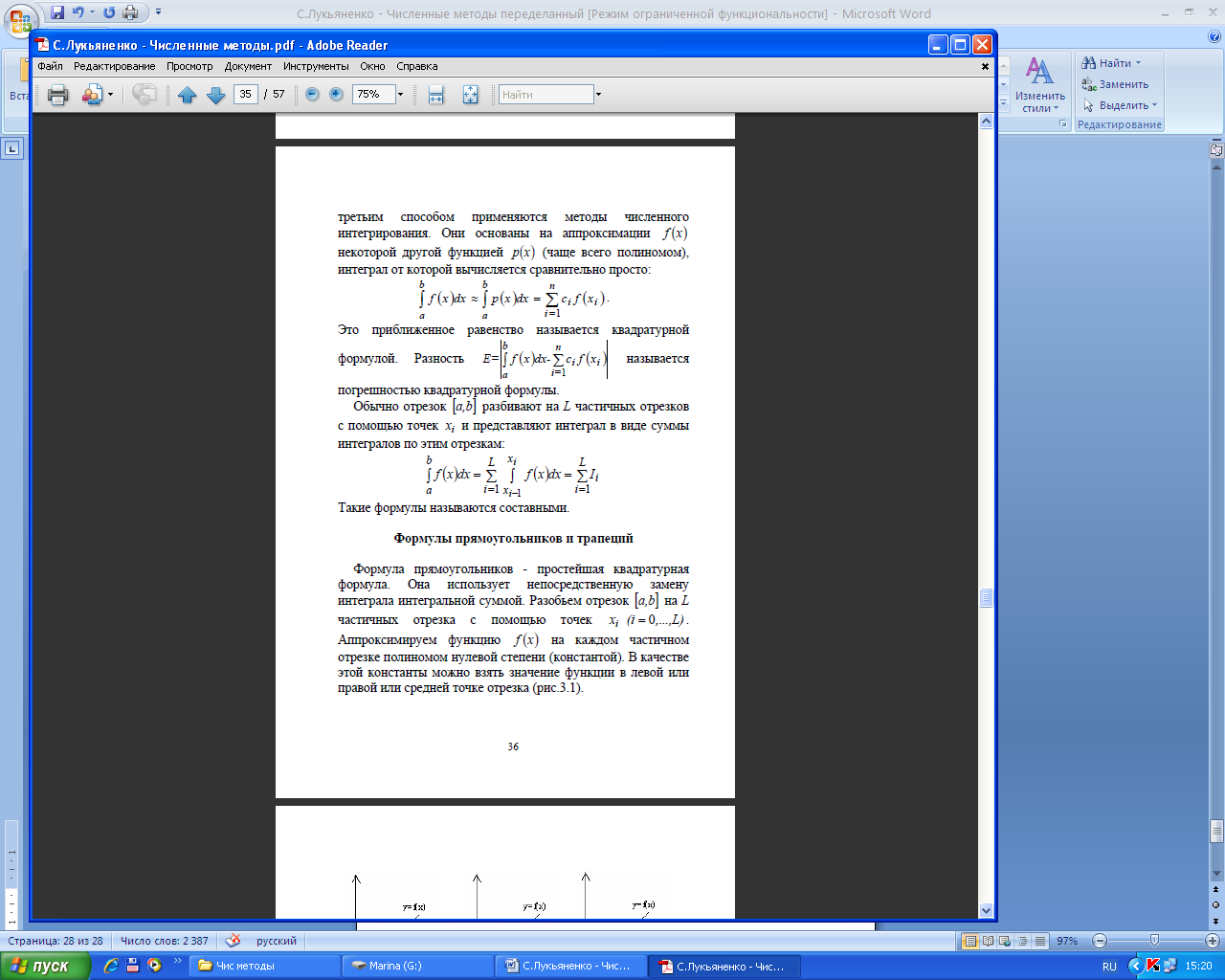
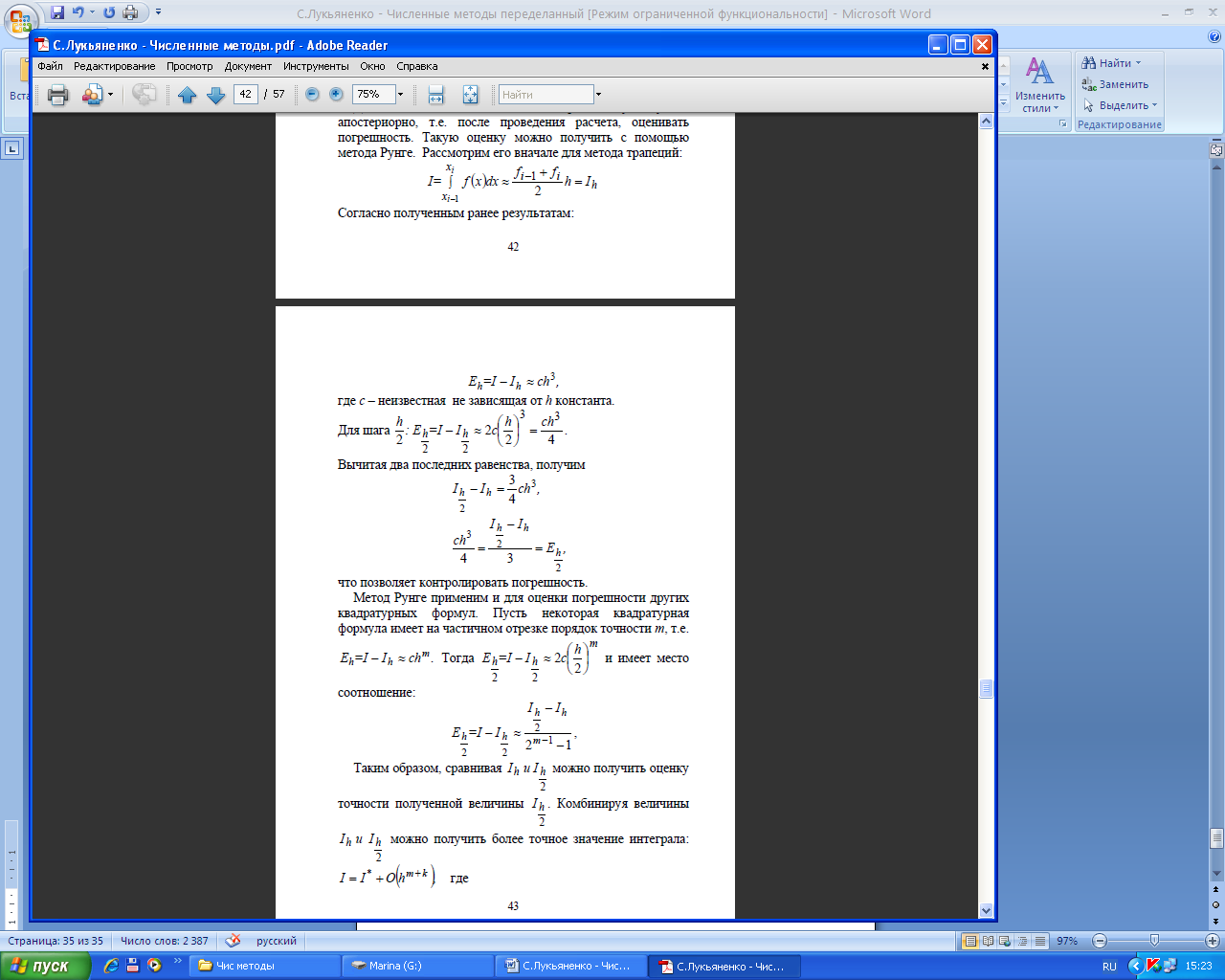
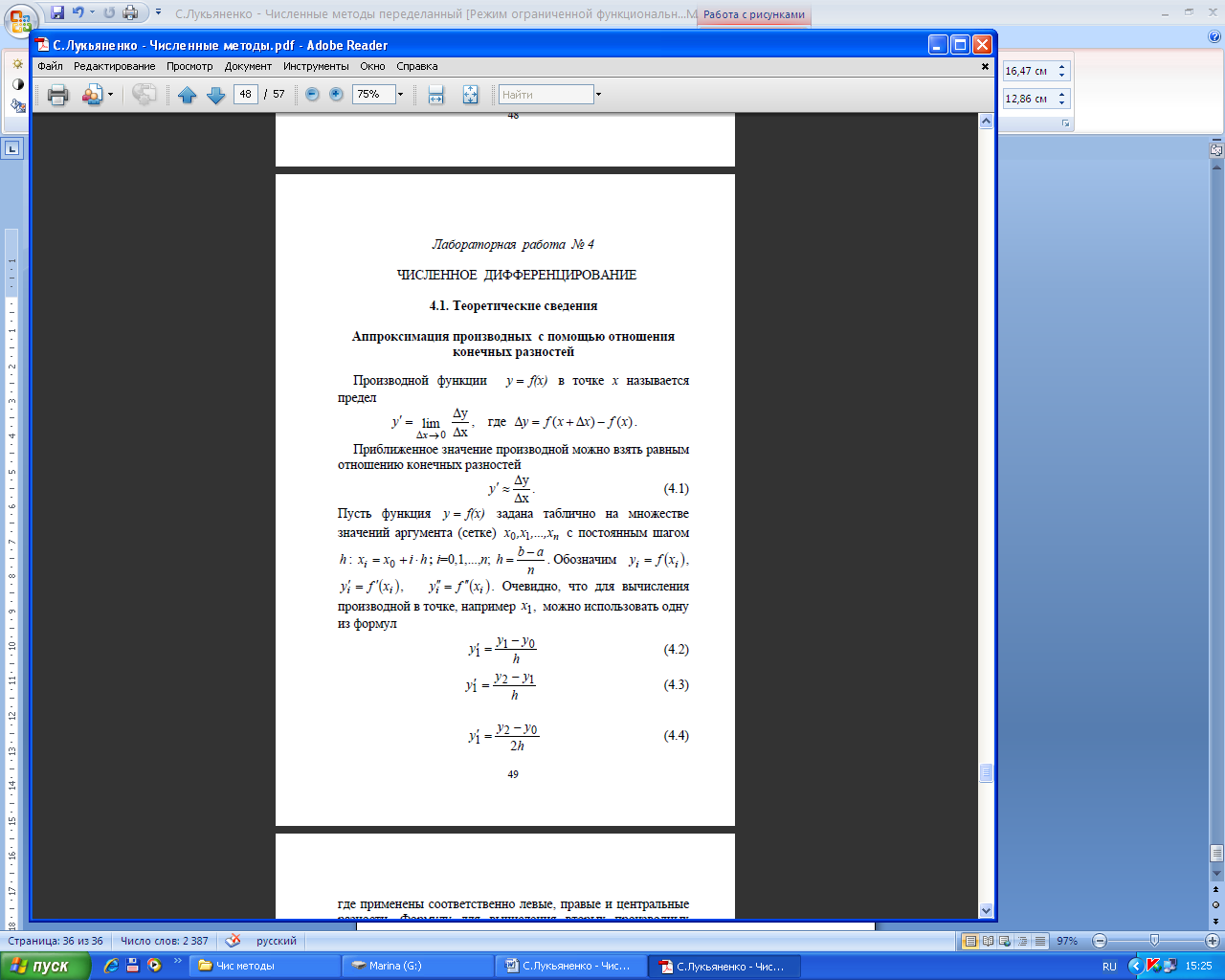
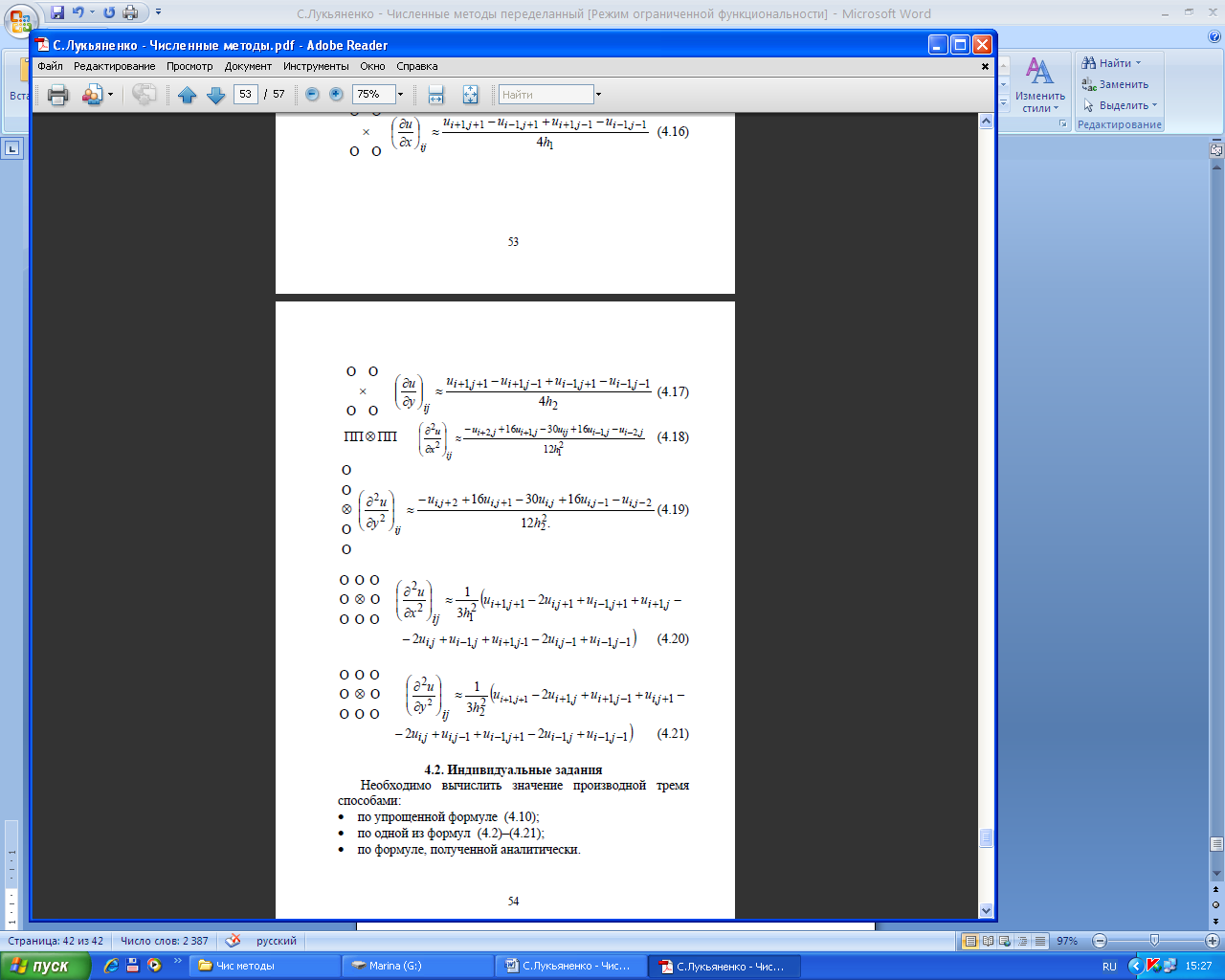
Метод обратной квадратичной интерполяции- экстраполяции

_{Заключается в замене}

_f(x)

_{полиномом Лагранжа второй}

степени (число узлов m=3). При этом можно получить аналитическое выражение для приближенного значения корня. Действительно, заменив x на y и y на x, полином Лагранжа второй степени можно представить в виде

^{x(y) = b}₀ ^{+ b}₁^{(y − y}₀ ^{) + b}₂^(y-y₀ ^{)(y − y}₁ ^{) .}

Для y=0 находим

^{x = b}₀ ^{− b}₁ ^y₀ ^{+ b}₂ ^y₀ ^y₁ ^{. (1.5)}

На следующей итерации, если выполняется

^{x − x}₁

^{> ε, задаем}

x₁ = x , если не выполняется, считаем x корнем.

Геометрическая интерпретация метода показана на рис. 1.7.

Метод поразрядного приближения

Алгоритм для поиска всех корней отрезка [a,b] этим методом имеет вид:

1. Задаем шаг С=h, x=a, k=0 и находим W=sign f(x) – знак функции.

^{2. Задаем значение x=x+С и проверяем условие (x-С) ≥ b.}

_{3. Если оно выполняется, заканчиваем счет, иначе - на п.4.}

_{4. Вычисляем f(x) и проверяем условие}

_{f ( x) ⋅W/C > 0 . Если}

_{оно выполняется, идем на п.2, иначе на п.5.}

_{5. Задаем}

_{C = −C/R , где R – показатель разрядности}

(уменьшения шага C), и проверяем выполнение условия C > е/R , где ε – заданная погрешность вычисления корня. Если это условие выполняется, идем на п.2, иначе на п.6.

6. Задаем k=k+1 и выводим на печать значение k-го корня

^x_k ^{= x . Затем полагаем C=h, W= -W и идем на п.2.}

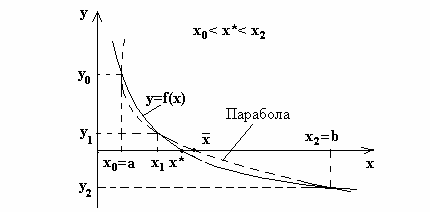
Рис. 1.7. Метод обратной квадратичной интерполяции-

экстраполяции

3