56. Основные законы гидродинамики

3.1. Уравнение неразрывности потока

Произведение средней скорости потока жидкости на площадь живого сечения при установившемся движении есть величина постоянная:

(1)

или

(2)

Уравнения (1) и (2) называются уравнениями неразрывности потока. На основании их можно сделать вывод, что при установившемся движении жидкости через любое живое сечение потока в единицу времени проходит одинаковое количество жидкости, т. е. для любых двух сечений потока массовый расход одинаков.

Массовый расход может быть представлен как

Уравнение неразрывности потока является первым основным законом гидродинамики и позволяет при известном секундном расходе определить скорость движения жидкости в любом сечении потока и наоборот — расход жидкости при известной скорости ее движения.

6.3.2. Уравнение Бернулли

Вторым основным законом гидродинамики является уравнение Бер­нулли, устанавливающее зависимость между скоростью и давлением в различных сечениях одной и той же струи (потока), причем эти сечения находятся на разной высоте относительно плоскости сравнения:

(3)

где 𝓏₁ и 𝓏₂ — высоты первого и второго сечений соответственно,

р₁ и р₂ — давления жидкости первого и второго сечений,

υ₁ и υ₂ — скорости потока первого и второго сечений.

В общем виде уравнение Бернулли может быть представлено как

(4)

Сумма двух слагаемых, входящих в это уравнение, называется полным напором в данном сечении.

Если уравнение (4) умножить на массу F жидкости, то получим

где первые два члена представляют собой потенциальную энергию массы движущейся жидкости, а третий член — кинетическую энергию.

Таким образом, уравнение Бернулли можно сформулировать следующим образом: полный напор или сумма потенциальной и кинетической энергии движущейся жидкости есть величина постоянная для всех сечений.

Но в отличие от идеальной жидкости при движении реальной возникают потери энергии (или напора). Причины этих потерь: трение о стенки трубопровода или канала, преодоление сил внутреннего трения в вязкой жидкости. Поэтому для потока реальной жидкости напор в первом сечении

всегда будет больше, чем напор в сечении, находящемся от него на некотором расстоянии:

Если величину указанных потерь энергии обозначить h_п, то уравнение Бернулли будет иметь вид:

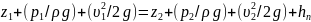
или

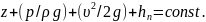
Различают два основных вида потерь:

• потери напора по длине трубопровода h_дл, обусловленные действием сил трения по поверхности канала на всех участках перемещения;

• потери местные h_м, обусловленные сопротивлением при про­хождении жидкости через изгибы, резкие сужения, расширения, отводы (тройники), краны, фильтры и т. п.

Таким образом

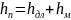
или

где ξ — коэффициент местного сопротивления определяется опыт­ным путем, для малых отверстий ξ = 0,06.

57. Истечение жидкости из малых отверстий и насадок

4 4.1. Истечение жидкости из малых отверстий

При выходе из малого отверстия (см. рис. 4, а) струя претерпевает сжатие. Сжатое сечение струи находится примерно на расстоянии 0,5d от стенки резервуара.

Отношение площади струи в сжатом сечении S_c к площади всего отверстия называется коэффициентом сжатия струи ε':

Опытным путем установлено, что ε'=0,64.

Составим уравнение Бернулли для сечений А—А и Б— Б.

Плоскость сравнения совпадает с осью сжатого сечения, тогда 𝓏₁ = Н, 𝓏₂ = 0, р₁ = р₂,υ₁ = 0, υ₂ = υ_c, h_м = ξυ²/2g.

Подставив эти уравнения в уравнение Бернулли, получим

где υ_с — скорость жидкости в струе.

Тогда

Обозначив множитель 1/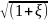 буквой φ, получим

(5)

где φ — коэффициент скорости. Опытным путем установлено, что φ = 0,97.

Для вычисления объемного расхода жидкости следует скорость умножить на площадь сжатого сечения:

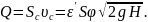
Произведение ε'φ называется коэффициентом расхода и обозначается буквой μ', тогда

(6)

где μ'= ε'φ ≈ 0,64 • 0,97 ≈ 0,62.

Массовый расход находится из уравнения

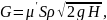(7)