37.Критические напряжения, гибкость стержней. Предел применимости формулы Эйлера. Формула Ясинского. Теорема Шенли.

До момента начала потери устойчивости стержни испытывают центральное сжатие, при котором в поперечном сечении равномерно распределенные нормальные напряжения, определяемые по формуле ,можно предположить, что и критические напряжения то же распределены равномерно и для определения их величины можно воспользоваться теорией центрального сжатия.

, где гибкость стержня, зависит от его геометрических размеров;

– радиус инерции поперечного сечения стоек.

Из полученного выражения следует, что критические напряжения зависят от упругой константы материала (Е) и гибкости бруса (λ).

Учитывая, что критическое напряжение не должны превышать предела пропорциональности ( ), легко можно определить предельную гибкость, т.е. ; .

В отличие от геометрической гибкости предельная гибкость ( ) зависит от физико-механических свойств материала, из которого изготовлена стойка.

Формула Эйлера применяется в тех случаях, когда действительная гибкость ( ) больше предельной( ). Если же гибкость сжатого бруса меньше предельной гибкости (λ< ), то критические напряжения и сила определяются по эмпирической формуле Ясинского:

$ , где aи b – коэффициенты, зависящие от материала.

38. Расчёт на устойчивость.

До момента потери устойчивости стержни испытывают центральное сжатие.

; ; ; ; ;

Выразим допускаемое:

- коэф-т изгиба; ; ;

; - по таблицам

Необходимо предварительно задаться одной из величин – или а. Чаще всего задают ; по этой величине коэф-та найдём ;

Для сконструированного сечения определяем центр тяжести, главн. моменты инерции, миним. моменты инерции, определим гибкость: i min= ; => 1*; если 1* отлично более 5% от принятого 1, то выполняем о тех пор, пока не выполнится условие ( 2= ;)

Конструирование сечения и выбор материалов при расчёте на устойчивость.

1)Поперечное сечение нужно конструировать таким образом, чтобы гл. моменты относительно обеих осей были одинаковы.

2)Конструировать сечение следует таким образом, чтобы А => min; Ix=Iy => max;

Осуществляем путём удаления А от центра

тяжести.

39. Продольно-поперечный изгиб.

Имеет место тогда, когда в поперечных сечениях брусьев, или эл-тов конструкции одновременно действуют изгиб моменты от поперечной и продольной нагрузок.

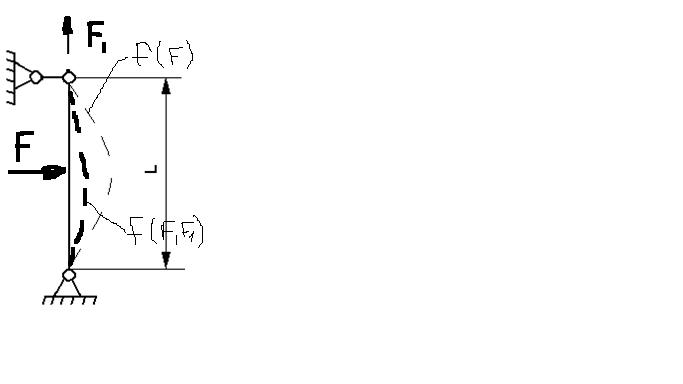
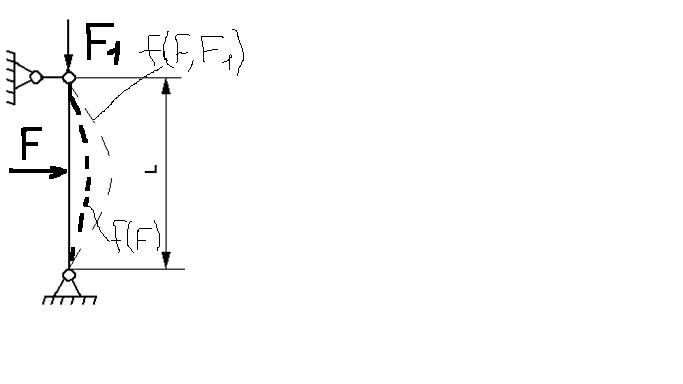
Оказывается, что зав-ть перемещений от продольной нагрузки нелинейная, т.е. она увеличивает прогибы или перемещения.

Расчёт массивных брусьев.

К массивным относят брусья, которые не склонны к потере устойчивости и по гибкости к 3-ей группе.

Принцип независ. действия силы.

;

40. Расчёт гибких стержней при продольно-поперечном изгибе.

К гибким относят те, которые склонны к потерям устойчивости. 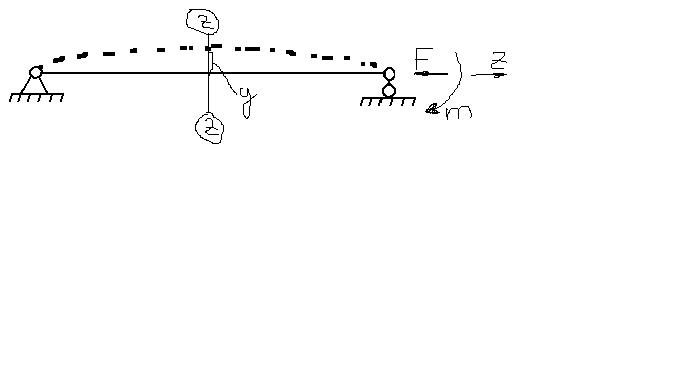M(z)=-m-F*y

Из получ. уравнения следует, что в него входят 2 неизвестные. Т.е. задача определения величины изгибающего момента является статически неопределимой, для её решения необходимо составить дополнительные ур-ния с учётом рассмотренных деф-ций.

E*I*y’’=M=-m-F*y; E*I*y’’+F*y=-m; y’’+k²*y= ; - дифуравн. изогнутой оси гибкого бруса, при продольно поперечном изгибе. k²= ; Решение является громоздким и трудоёмким.

Для приближённого решения полученное ДУ введём следующие ограничения:

1. Продольные и поперечные нагрузки изгибают эл-т в одном направлении.

2. Поперечные нагрузки приложены к стержню относительно опор.

3. Будем считать, что изогнутая ось обозн. синусоидой.

От поперчн. – f₀

От поперечн. и продольн. – f

- определение макс. прогиба при продольном и поперечном изгибе. fo – поперечный прогиб ; F – продольная нагрузка ; Fкр. – критическая сила;

Исследование влияния на прогиб продольной силы.

Необходимо произвести алгебраическое суммирование от составл. силовых факторов.

; Mx(F)=F*f;

При расчёте на прочность необходимо задаваться дополнительным коэф-том запаса по прочности силы F.