30.Определение положения нулевой линии при внецентренном сжатии, её св-ва.
Нулевая линия – линия во всех точках которой нормальное напряжение сигма равно нулю. Для определения положения нулевой линии вычисляют отрезки отсекаемые ей на осях координат.
ax=-iy2/xF ay=-ix2/yF
31. Расчет на прочность при внецентренном сжатии. Ядро сечения
σmax
=
≤[σp]
Если е - мало, то тогда Мх и Му принебрегают и условие прочности записывают так
σmax=
;
Если е - велико, то тогда принебрегают F и условие прочности записывают так
σmax
=
Ядро сечения – область вокруг центра тяжести, прикладывая внешнюю силу в которую во всем сечении напряжения будут иметь один знак.
Для построения ядра сечения полагают, что нулевые линии должны касаться контура сечения и ни в коем случае не пересекать его
Для
построения ядра сечения используем
формулы нулевых линий, по которым
выражаем
и
32. Изгиб и кручение круглых стержней. Определение напряжений
Встречается в технике при передаче крутящего момента с вала двигателя на приемные устройства
Под действием изг момента воникают σ, под действием крутящего момента Т – τ
Главные напряжения:
33. Расчет на прочность при изгибе с кручением круглых стержней
Оценку прочности следует проводить с учетом одной из теорий прочности, т.к. в опасных точках имеет место плоское напряженное состояние
первая
теория: σr1=
Mрасч1/Wx1≤R;
Mрасч1=
вторая
теория: σr2=
Mрасч2/Wx2≤R;
Mрасч2=
третья
теория: σr3=
Mрасч3/Wx3≤R;
Mрасч3=
четвертая
теория: σr4=
Mрасч4/Wx4≤R;
Mрасч4=
34. Изгиб и кручение стержней прямоугольного сечения.
Мы воспользуемся следующей формулой
Для
проверки прочности элемента, выделенного
в окрестности опасной точки, необходимо
выбрать соответствующую теорию
прочности. Например, по теории наибольших
касательных напряжений:
По теории прочности Мора:
для вала круглого и кольцевого сечения Wp=2Woc
3
5.
Кручение и растяжение круглых стержней.
Под
действием сил F
действует центральное напряжение δ
под действием момента Т возникает
деформация кручения и в поперечных
сечениях будут возникать касательные
напряжения.
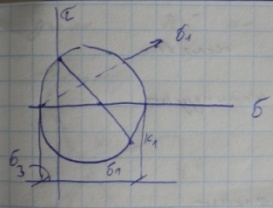
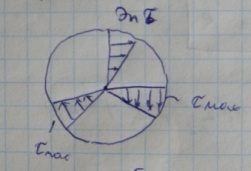
τ
δ
36. Устойчивость сжатых стержней. Формула Эйлера. Учёт различных видов закрепления стержней.
При
сравнительно небольшом значении
сжимающей нагрузки F
стержень испытывает сжатие и находится
в состоянии устойчивого равновесия,
т.к., получив малое искривление
геометрической оси за счёт поперечного
усилия, стержень быстро возвращается
в исходное положение. По мере увеличения
сжимающей нагрузки F
стержень всё медленнее возвращается
в первоначальное положение после
поперечного усилия и при некотором
критическом значении
наступает состояние безразличного
равновесия: после самостоятельного
искривления стержень приобретает
равновесие и в искривленном состоянии.
Происходит раздвоение равновесия:
прямолинейная форма теряет устойчивость,
а криволинейная ещё не успевает её
приобрести, которая теоретически
становится устойчивой при
.Формулу
для определения величины критической
силы для стойки, шарнирно закреплённой
обоими концами, впервые(1744 г) получил
Л.Эйлер, она имеет Вид:
, т.е величина критической силы прямо
пропорциональна жесткости (EI)
и обратно пропорциональна квадрату
длины стойки(L).
Для различных случаев закрепления
концов сжатых стоек величину критической
силы определяем по формуле в виде:
,где µ - коэффициент приведенной длинны,
а величина
- приведенная длина.