
- •1. Изгиб. Балки. Построение эпюр q,m.
- •2. Диф. Зависимость между q, q, m
- •3. Чистый изгиб. Определение нормальных напряжений
- •4. Кривизна балок. Осевые моменты сопротивлений
- •5. Расчет на прочность при чистом изгибе. Потенциальная энергия деформации
- •6. Плоский поперечный изгиб. Определение касательных напряжений
- •7. Определение касательных напряжений в балках сплошных поперечных сечений. Эпюр τ.
- •8.Определение касательных напряжений в двутавровых балках, их эпюр.
- •9.Исследование напряжённого состояния балок при плоском поперечном изгибе балок.
- •10. Главные напряжения при плоском поперечном изгибе балок, их траектории.
- •1 1. Расчет балок на прочность по методу двух допускаемых напряжений.
- •12. Упруго-пластический изгиб балок.
- •13.Инженерные методы расчетов балок.
- •14.Изгиб балок переменного сечения
- •15. Изгиб балок с разными модулями упругости при растяжении и сжатии.
- •16. Понятие о центре изгиба
- •17. Деф. Балок. Ду упругой линии
- •18. Опред. Перемещений балок методом непосредственногоинтегрир. Ду.
- •19 Вывод универсальных уравнений перемещений в балках.
- •20 Определение начальных параметров.
- •21 Определение перемещений в балках графоаналитическим методом(метод фиктивных балок).
- •22.Определение перемещений балок переменного сечения (равного сопротивления)
- •23.Потенциальная энергия деформации при плоском поперечном изгибе.
- •24.Статически неопределимые балки, их расчёт. Многопролётные балки.
- •25. Расчет статически неопределимых балок по разрушающим нагрузкам.
- •26. Сложное сопротивление
- •27. Определения положения нейтральной оси.
- •28. Определение перемещений при косом изгибе.
- •29.Внецентренное сжатие-растяжение, определение растяжений.
- •30.Определение положения нулевой линии при внецентренном сжатии, её св-ва.
- •31. Расчет на прочность при внецентренном сжатии. Ядро сечения
- •37.Критические напряжения, гибкость стержней. Предел применимости формулы Эйлера. Формула Ясинского. Теорема Шенли.
- •38. Расчёт на устойчивость.
- •39. Продольно-поперечный изгиб.
- •40. Расчёт гибких стержней при продольно-поперечном изгибе.
- •41.Расчет стержней при продольно-поперечном изгибе в случае внецентренного приложения продольной силы.
- •42.Динамические нагрузки. Типы нагрузок. Расчет на инерционные нагрузки.
- •43 Продольный удар по брусу.
- •44.Поперечный удар
- •45. Учёт собственного веса бруса при ударе.
- •46.Расчет при напряжениях переменных во времени. Характеристика циклов переменных напряжений. Усталость материалов.
- •47.Испытание материалов на усталость. Предел выносливости. Влияние на величину предела выносливости различных факторов.
- •48.Диаграмма предельных циклов. Расчет на выносливость.
- •49. Расчёт кривых брусьев. Построение эпюр n, q, m. Определение напряжений от n, q.
- •50. Определение напряжения при чистом изгибе кривых брусьев.
18. Опред. Перемещений балок методом непосредственногоинтегрир. Ду.
Чтобы
получить ур-ние углов поворота попер.сеч.
необходимо приближ. ДУ проинтегрировать
1 раз:
C и D– постоянные интегрирования опред. из рассмотрения условий на границах силовых участков или на опорах.

Перемещение свободного конца балки- ?




Для определения С и D воспользуемся, что при z=L, уА=о; А=0


Подставив С иD в уравнение
19 Вывод универсальных уравнений перемещений в балках.
Пример:

- имеем пять силовых участков. Если считать по методу непосредственного интегрирования, то получим 10 постоянных.
Вычислим момент в сечении 1.
1) M1=0, подставим в диф. уравнение
y1”EI=0, интегрируем 1-й раз.
1EI= +С1, интегрируем во2-й раз.
y1EI= С1 Z1 – D
0 ≤ Z1 ≤ a
если Z1=0, то С1=0EI; D1=y0EI – т.е. мы сразу нашли начальные параметры.
Нам нужно доказать, что на любом участке Сn и Dn = величинам 0EI и y0EI.
2) M2= -m(z2 - a)0,
y2”EI= m(z2 - a)0,
2EI= m(z2 - a)0+С2,

3) M3= -m(z3 - a)0- F(z3 - b),
y3”EI= m(z3 - a)0 + F(z3 - b),
 ,
,
 4)
4)
 ,
,
 ,
,
 ,
,
 5)
аналогично ……………
5)
аналогично ……………
На границах силовых участков:
Z1 = Z2 C1 = C2; D1 = D2
Z2 = Z3 C2 = C3; D2 = D3
Z3 = Z4 C3 = C4; D3 = D4
Zi = Zi=1 Ci = Ci+1; Di = Di+1
Если все задачи решать т.к. мы решали данный пример, то значит
C1 = C2 = C3 = ….= Ci = Ci+1 = 0EI
D1 = D2 = D3 = ….= Di = Di+1 = y0EI
В окончательных формулах, выражения в скобках (Zi - ai) заменены соответственно расстояниями Z.
20 Определение начальных параметров.
При использовании метода начальных параметров для различных балок доказали что

m,F,q в этих уравнениях независимо от того , сколько их записано в балке силы записываются одинаково.
 обозначим
отрезками z
от соответствующих сил до сечения, где
определяется прогиб, получим универсальное
уравнение
обозначим
отрезками z
от соответствующих сил до сечения, где
определяется прогиб, получим универсальное
уравнение

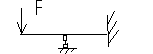
Выясним, как определять начальные параметры
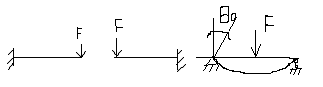


 определили
из граничного условия, что
определили
из граничного условия, что





21 Определение перемещений в балках графоаналитическим методом(метод фиктивных балок).
YEI-прогиб

интенсивность распределённой нагрузки
Мор установил аналогию, что для перехода от изгибающего момента к прогибу (изгибающий момент берется из эпюры), нужно выполнить аналогичные операции, как при переходе от интенсивности распределенной нагрузки к изгибающему моменту.
Для того, чтобы найти прогиб, надо момент представить, как q

Для того чтобы воспользоваться полученными функциями по аналогии Мора необходимо
1.построить эпюру «М» для заданной балки
2.заменить реальную балку, для которой построен эпюр «М" фиктивной балкой.
3.к фиктивной балке приложить фиктивную нагрузку, которая является эпюрой моментов.
![]() действительная
балка
действительная
балка
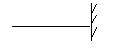 фиктивная
балка
фиктивная
балка
![]() действительная
балка
действительная
балка
![]() действительная
балка
действительная
балка
![]() фиктивная
балка
фиктивная
балка
 фиктивная
балка
фиктивная
балка
Примеры:


Когда нужно найти промежуточные значения, то этот метод не очень удобен.


