49. Расчёт кривых брусьев. Построение эпюр n, q, m. Определение напряжений от n, q.

Построение эпюр

для криволинейных стержней

В поперечных сечениях плоского кривого бруса могут действо­вать, как и в рамах, три внутренних силовых фактора — N, Q и М. Наиболее часто имеют дело со стержнями, ось которых очерчена по дуге окружности. В этом случае положение любого сечения удобно определять при помощи полярной системы координат, тогда продольная, поперечная силы и изгибающий момент будут функ­циями угла ф: N(ф), Q(ф) и M(ф).

Для N и Q примем обычное правило знаков , эпюры М будем, как и в рамах, строить на сжатых волокнах.

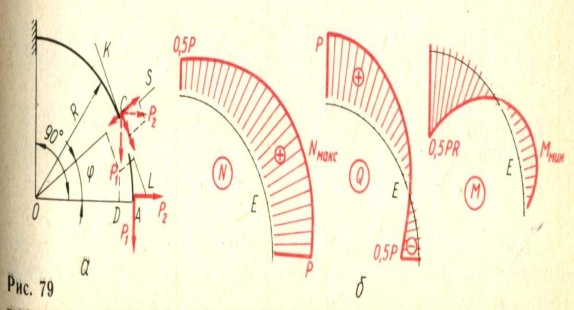
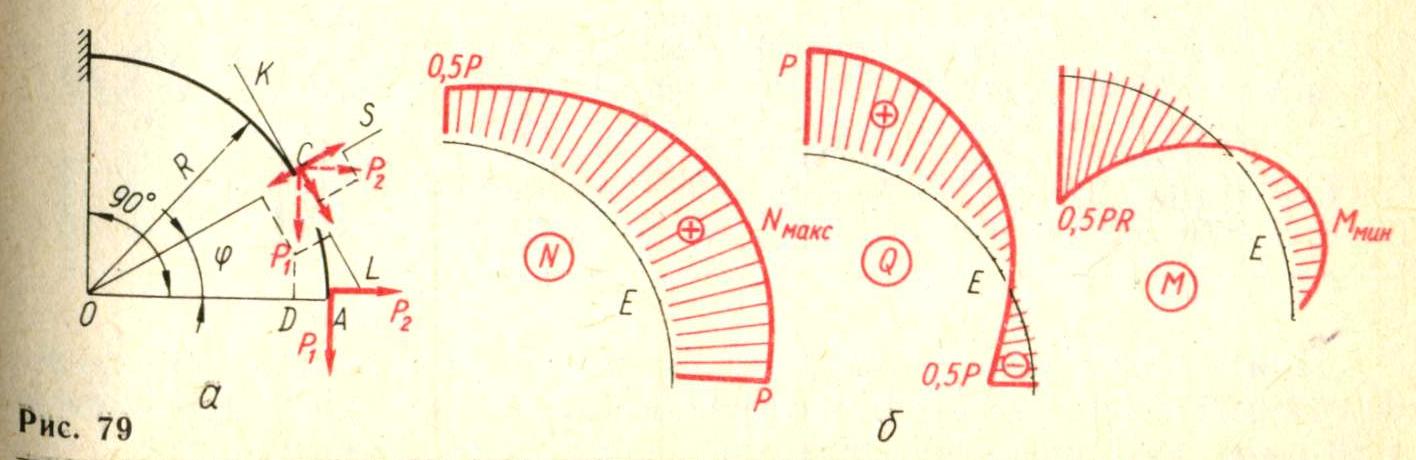
В качестве примера рассмотрим плоский кривой брус, схема которого показана на рис. 79, а. Напишем значения N(ф), Q(ф) и М (ф) для произвольного сечения С.

Чтобы получить N(ф), нужно силы P1 и Р₂ спроецировать на направление оси стержня в точке С, т. е. на касательную KL. Для удобства проецирования их можно перенести мысленно в точку С (на рис. 79, а они показаны штриховыми линиями). Тогда

N (ф) = P1 cos ф + Р2 sin ф.

Чтобы получить Q(ф), нужно спроецировать силы, приложен­ные к части АС, на плоскость сечения, т. е. на направление OS:

Q (ф) = P1 sin ф — Р₂ cos ф.

При составлении выражения для изгибающего момента в произ­вольном сечении условимся, например, считать изгибающий момент положительным, если он вызывает сжатие волокон, лежащих с внут­ренней стороны стержня (т. е., если он увеличивает кривизну стерж­ня). Будем иметь

M(ф)=P_lAD — P₂ CD = P_lR(1 —cos (ф)-P₂R sin ф.

Правило знаков: N Растяжение «+», сжатие «-»

Q Сдвиг по ходу часовой «+», против – «-» Если направление Q получается путём поворота положит. напр. N на угол 90, то «+»

M Если под действием момента увелич. кривизна бруса «+», уменьшается – «-».

Под действием нормальной силы в поперечном сечении криволинейных брусьев аналогично прямым возникают равномерно распределённые нормальные напряжения.

50. Определение напряжения при чистом изгибе кривых брусьев.

Частный случай прямого изгиба, при котором в поперечном сечении действует только изгибающий момент – чистый изгиб.

С помощью метода сечений рассмотрим равновесие бруса под действием изгибающего момента М и внутренних сил, действующих поперечно сечению

Задача определения норм. напряжения статически неопределима. Для её решения надо составить ур-е деформации. Рассмотрим слой на расстоянии y с радиусом кривизны . Сечение оставаясь плоским повернётся на угол . Удлинение слоя ab (бесконечно малый эл-т бруса) . . Слои испытывают только прямое раст. или сжат. По закону Гука: . Подставляем выр-е . Закон изменения напряжения гиперболический.

Рассмотрим решение полученного интеграла, в который вместо координаты подставим разность .

В итоге получим:

51. Определение положения нейтральной оси в кривых брусьях. Расчёт на прочность.

Для определения радиуса кривизны нейтрального слоя воспользуемся уравнением равновесия, из которого следует:

Где h – высота поперечного сечения

Расчёт на прочность сводится к составлению условий прочности по нормальным и касательным напряжениям, иногда по главным.