41.Расчет стержней при продольно-поперечном изгибе в случае внецентренного приложения продольной силы.
Рассм. брус
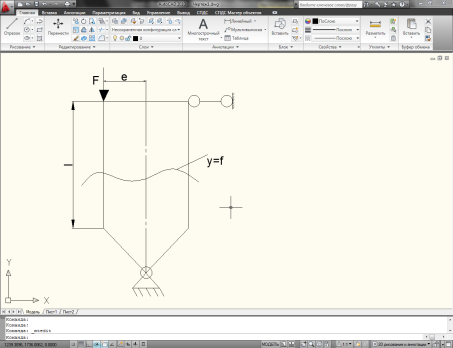
1) Устанавливаем, что в поперечном сечении действует нормальная сила N=-F
2) Mx=FL
3)Mx(F)=Ff
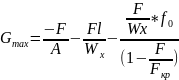
Для составления условия прочности, учитывая что продольная сила F нелинейно влияет на G необходимо также дополнительно задаваться коэффициентом запаса прочности по продольной силе F
42.Динамические нагрузки. Типы нагрузок. Расчет на инерционные нагрузки.
При изучении всех видов деформации предполагалось, что элементы конструкции нагружаются статически, т.е. нагрузками величина которых изменяется от 0 до конечных с незначительными скоростями увеличения, при этом в дальнейшем оставаясь сonst. На практике в большинстве случаев нагружения элементов конструкции осуществляется в незначительном промежутке времени, при этом возникают ускорения отдельных точек элементов и сопутствующие им силы инерции.
Расчёт на динамические нагрузки сводится к определению величины динамического коэффициента. Определим динамический коэф. напряжения или перемещения легко получится с учётом следующей зависимости
;
;
Динамические характеристики определяются теоретически или экспериментально.
Мех. характеристики возр., а хар-ки пластичности уменьшаются
Разность в характеристиках заключается за счёт распространения волны деформации
Динам. нагрузки подразделяются на
а) инерционные
б) ударные
Рассмотрим расчёт троса или каната подъёмного устройства движущегося с ускорением а. Требуется определить усилие троса в сечении
При
статическом нагружении:
Очевидно, что сила инерции направлена вниз
,
-
динамический коэффициент
43 Продольный удар по брусу.
1.В процессе удара бруса Q происходит абсолютно неупругий удар ,т.е. отсутствует отскок.
2. Кинетическая энергия бруса полностью переходит в потенциальную энергию динамической деформации.
T=Uд=Aд (T-кинетическая эн-я)
T=Q*(H+δд)=Uд
Uст=
*δ2ст*с;
с=
Uд= *δ2д*с= * δ2д*
* δ2д* - Q*(H+δд)=0
δ2д-2*δд*δст-2*H* δст=0
δд=
δст+
δд=δст*kд
kд=1+
определение дин-го коэф-та при продольном
ударе
H-высота падения бруса
δст.-стат-я деформация бруса от внеш. нагрузки
44.Поперечный удар
fст=
*l3
kд=1+
fд=fст*kд= *l3*(1+ )
45. Учёт собственного веса бруса при ударе.
В некоторых случаях при ударных нагрузках влияние собственного веса ударяемых эл-ов оказывают существенное влияние на величину дин-го коэф-та kд. В этих случаях необходимо в общее ур-е энергии добавить энергию эл-в в процессе удара, задача определения kд в таких случаях является сложной и трудоёмкой ,поэтому используют приближённый метод ,заключающийся в том, что вместо распределённой массы эл-в, на которые наносится удар, используют приведенную массу, которую прикладывают в сечениях, по которым наносится удар.
Ф-ла
определения kд:
kд=1+
k-коф-т приведенной массы
G-собственный вес бруса
Q-вес падающего бруса
H-высота падения бруса
δст.-стат-я деформация бруса от внеш. нагрузки
Расчёт на прочность и жёсткость при дин-х нагрузках.
Условие прочности и жёсткости при дин-х нагрузках составляется аналогично, условию прочности для статических нагрузок :
σдин=σст*kд
[σ]д
σ=
[σ]=
σоп=(σy;σu)
[σ]д=
fд=fст*kд [f]д
fд- дин-е перемещение
fст- перемещение при статическом нагружении
kд- дин-й коэф-т
[f]д- допускаемая величина перемещения при нагружении