1. Изгиб. Балки. Построение эпюр q,m.
Изгиб широко встречается в инженерной практике, например: изгиб балок, изгиб рам, изгиб осей, изгиб валов
Стержни, работающие преимущественно на изгиб, принято называть балками. При изгибе часть волокон, расположенных по высоте балке, испытывает растяжение, а часть сжатие. В зависимости от способов приложения нагрузки и способов закрепления стержня могут возникать различные виды изгиба: чистый, поперечный и др.
Различают 3 типа опор:
Шарнирно-неподвижная опора; шарнирно-подвижная, жесткая заделка.
Построение эпюр Q, M: для этого необходимо определить опорные реакции, выявление силовых участков, силовой участок – участок на котором внутренние силы изменяются по одному закону используя метод сечений и правило знаков составить аналитические выражения для Q, M, вычислить значения Q, M в характерных сечениях балки. По результатам расчёта строим эпюры Q, M.
2. Диф. Зависимость между q, q, m
Для проверки правильности построения эпюр Q, M используются дифференциальные зависимости:
Q
3. Чистый изгиб. Определение нормальных напряжений
Определение нормальных напряжений при чистом изгибе.
При изгибе возникают изгибающий момент и поперечная сила, чистый изгиб – это частный случай изгиба, при котором поперечная сила равна нулю.
Воспользуемся для определения нормального напряжения при чистом изгибе законом Гука при растяжении сжатии.
=
ℇ
ℇ=
=
;
В
нашем случае
;
о
;
,
п
олучим:
Сжатие «-», растяжение «+»;
4. Кривизна балок. Осевые моменты сопротивлений
-
формула, выражающая кривизну балки.
а) прямоугольник
Wx=Ix/ymax
Ix=bh3/12
ymax=h/2
Wx= bh3*2/12h=bh2/6
Аналогично Wу
б) круг
Wx=Ix/ymax
Ix= Iу=πR4/4
ymax=R
Wx= Wy= πR3/4
5. Расчет на прочность при чистом изгибе. Потенциальная энергия деформации
σmax=Mx/Wx≤[σ] ±2-5%
3 типа задач:
1)проектная Wx= Mx/[σ]
2)определение грузоподъемности Mx≤ Wx[σ]
3)проверочная σmax=Mx/Wx≤[σ] ±2-5%
Когда балки неодинак сопротивляются раст/сжат составляют 2 условия прочности σmax=Mx/Wx≤[σ]р
σmax=Mx/Wx≤[σ]сж
Силовой фактор – изгибающий момент Mx
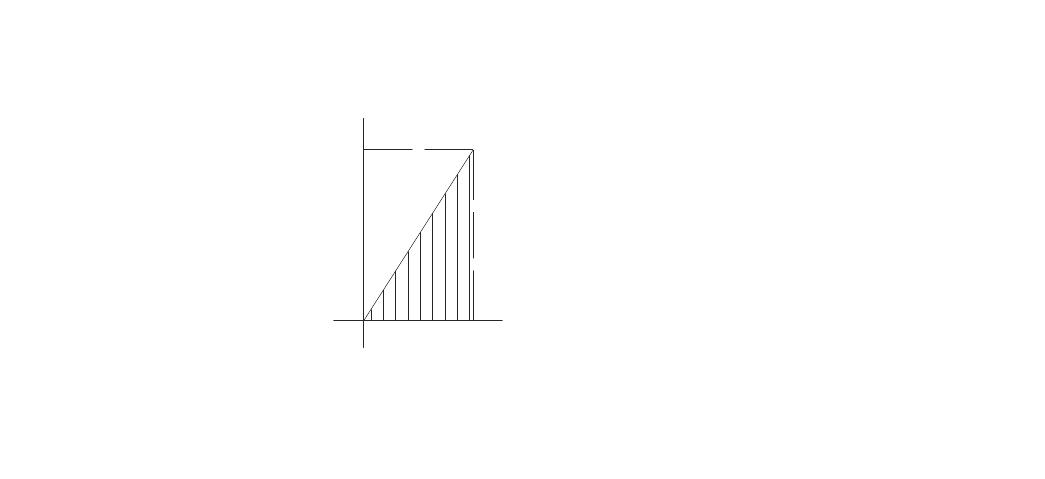
M
dα
dA=1/2* M dα
dα=dz/ρ
ρ= Mx/EIx
A=
A=U=M2l/2EI
6. Плоский поперечный изгиб. Определение касательных напряжений
ППИ возникает тогда, когда на поперечное сечение балки действуют одновременно изг момент Mx и поперечная сила Qx или Qy. Под действием Mxвозникают норм. напр-я σ, а под действ Q касс напр-я.
Используется теория чистого изгиба:
σ=Mxy/Ix≤[σ]р
σmax,min=Mx/Wx
σmax,min=±Mx/Wx≤[σ]
N1=
,
σ1=Mxy/Ix
N1=
=Mx/Ix
=
MxSxотс/Ix
N2=
=
=(Mx+dM/Ix)Sxотс
T= τ*dz*b
Σz=0
N1+T-N2=0
MxSxотс/Ix+ τ*dz*b-(Mx+dM/Ix)Sxотс=0
;
-
формула Журавского
для определения касательных напряжений.