20 Пружинный, физический и математический маятники.

Математический маятник

Это материальная точка, подвешенная на тонкой нерастяжимой и невесомой нити.Если отклонить маятник от положения равновесия, то сила тяжести и сила упругости будут направлены под углом. Равнодействующая сила уже не будет равна нулю. Под воздействием этой силы маятник устремится к положению равновесия, но по инерции движение продолжится и маятник отклоняется в другую сторону. Равнодействующая сила его снова возвращает. Далее процесс повторяется. Период колебаний математического маятника зависит от его длины, определяется по формуле

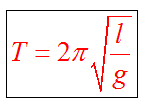
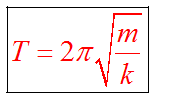
Пружинный маятникЭто груз, прикрепленный к пружине, массой которой можно пренебречь.Пока пружина не деформирована, сила упругости на тело не действует. В пружинном маятнике колебания совершаются под действием силы упругости. Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной ocи (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести. В отличие от математического маятника массу такого тела нельзя считать точечной. При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

21 Сложение гармонических колебаний одного направления и одинаковой частоты. Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания не­обходимо сложить. Сложим гармониче­ские колебания одного направления и оди­наковой частоты

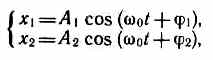
воспользовавшись методом вращающего­ся вектора амплитуды (см. § 140). Постро­им векторные диаграммы этих колебаний (рис.203). Так как векторы a1 и А2 вра­щаются с одинаковой угловой скоростью ₀, то разность фаз (₂-₁) между ними остается постоянной.

Очевидно, что уравнение результирующего колебания будет х=х₁+х₂=Аcos(₀t+). (144.1)

В выражении (144.1) амплитуда А и начальная фаза  соответственно за­даются соотношениями

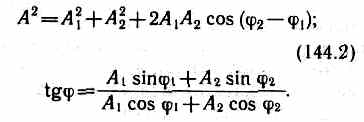
Таким образом, тело, участвуя в двух гар­монических колебаниях одного направле­ния и одинаковой частоты, совершает так­же гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (₂-₁) складываемых ко­лебаний.

Проанализируем выражение (144.2) в зависимости от разности фаз (₂-₁):

1) ₂-₁=±2m (m = 0, 1, 2,...), тог­да A=A₁+A₂, т.е. амплитуда результирующего колебания А равна сумме ампли­туд складываемых колебаний;

2) ₂-₁= ±(2m+1) (m=0, 1, 2,...), тогда A = │A₁-A₂│, т.е. амплиту­да результирующего колебания равна разности амплитуд складываемых коле­баний.

22 сложение взаимно перпендикулярных колебаний

Рассмотрим результат сложения двух гар­монических колебаний одинаковой часто­ты , происходящих во взаимно перпенди­кулярных направлениях вдоль осей х и у. Для простоты начало отсчета вы­берем так, чтобы начальная фаза первого колебания была равна нулю: Разность фаз обоих колебаний равна , А и В — амплитуды складываемых коле­баний.Уравнение траектории результирую­щего колебания находится исключением из выражений (145.1) параметра t. За­писывая складываемые колебания в виде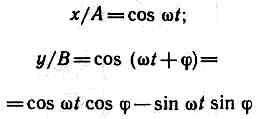

и заменяя во втором уравнении cost на х/А и sint на (1-(х/A)²), получим по­сле несложных преобразований уравнение эллипса, оси которого ориентированы относительно координатных осей произ­вольно:

Так как траектория результирующего ко­лебания имеет форму эллипса, то такие колебания называются эллиптически по­ляризованными.Ориентация осей эллипса и его разме­ры зависят от амплитуд складываемых колебаний и разности фаз . Рассмотрим некоторые частные случаи, представляю­щие физический интерес:

1) =m(m=0, ±1, ±2,...). В дан­ном случае эллипс вырождается в отрезок228

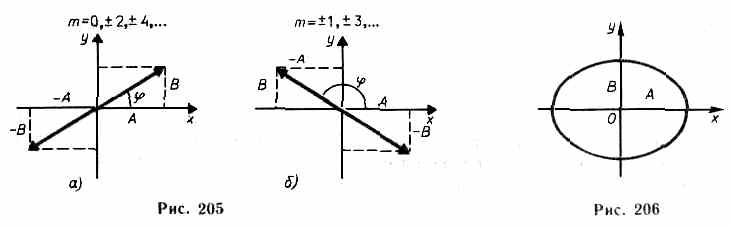
Прямой у=±(В/А)х, (145.3) где знак плюс соответствует нулю и четным значениям т (рис. 205, a), a знак минус — нечетным значениям т (рис. 205, б). Результирующее колеба­ние является гармоническим колебанием с частотой  и амплитудой (A²+В²), совершающимся вдоль прямой (145.3), составляющей с осью х угол =

В данном случаеимеем дело с линейно поляризованными колебаниями.

В данном случае уравнение примет вид

23 Продольные и поперечные волны. Уравнения бегущей волны

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распростра­нении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передаются лишь состояние колебательного движения и его энергия. Поэтому основным свойством всех волн, независимо от их природы, яв­ляется перенос энергии без переноса ве­щества. Упругие волны бывают продольные и поперечные. В продольных волнах части­цы среды колеблются в направлении рас­пространения волны, в поперечных — в плоскостях, перпендикулярных направ­лению распространения волны.

Продольные волны могут распро­страняться в средах, в которых возника­ют упругие силы при деформации сжа­тия и растяжения, т. е. твердых, жидких и газообразных телах. Поперечные во­лны могут распространяться в среде, в которой возникают упругие силы при деформации сдвига, т. е. фактически только в твердых телах; в жидкостях и газах возникают только продольные волны, а в твердых телах — как про­дольные, так и поперечные.

Бегущими волнами называются волны, ко­торые переносят в пространстве энергию. Для вывода уравнения бегущей во­лны — зависимости смещения колеблю­щейся частицы от координат и времени — рассмотрим плоскую волну, предполагая, что колебания носят гармонический ха­рактер, а ось х совпадает с направлением распространения волны (рис. 220). В дан­ном случае волновые поверхности перпен­дикулярны оси х, а так как все точки волновой поверхности колеблются одина­ково, то смещение  будет зависеть только от х и t, т. е. =(х, t).

уравнение колебаний частиц, лежащих в плоскости х, имеет вид (x,t)=Acos(t-x/v), откуда следует, что (х, t) является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (154.1) есть уравнение бегу­щей волны. Если плоская волна распро­страняется в противоположном направлении, то (х, t)=A cos(t+x/v).