₁

Механическое движение является простейшим видом движения в природе. Оно заключается в изменении взаимного положения тел или частей одного и того же тела в пространстве с течением времени. Материальной точкой называют тело, размерами которого в конкретной физической задаче можно пренебречь, а всю массу тела считать сконцентрированной в этой точке. Материальная точка является идеальной физической моделью реального тела, которое рассматривается в конкретной задаче. Механическое движение тела является относительным, поскольку оно всегда происходит как движение одного тела относительно другого, которое условно считается неподвижным.

Для характеристики движения материальной точки вводится векторная величина — скорость, которой определяется как быстрота движения, так и его направ­ление в данный момент времени.

Пусть материальная точка движется по какой-либо криволинейной траектории так, что в момент времени t ей соответствует радиус-вектор r0(рис 3) В течение малого промежутка времени Dt точка пройдет путь Ds и получит элементарное (бесконечно малое) перемещение Dr.

Вектором средней скорости <v> называется отношение приращения Dr радиуса-вектора точки к промежутку времени Dt: Направление вектора средней скорости совпадает с направлением Dr. При неограниченном уменьшении Dt средняя скорость стремится к предельному значению, которое называется мгновенной скоростью v: Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущейся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касательной к траектории в сторону движения (рис. 3). По мере уменьшения Dt путь Ds все больше будет приближаться к |Dr|, поэтому модуль мгновенной скорости Таким образом, модуль мгновенной скорости равен первой производной пути по времени: При неравномерном движении — модуль мгновенной скорости с течением времени изменяется. В данном случае пользуются скалярной величиной ávñ — средней скоростью неравномерного движения:

2 Ускорение мат. Точки. Норальноеи тангенциальное ускорения

Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло. Если скорость изменяется одинаково в течение всего времени движения, то ускорение можно рассчитать по формуле

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

Тангенциальное ускорение, касательное ускорение, составляющая ускорения, направленная по касательной к траектории тела. Величину тангенциального ускорения — в смысле проекции вектора ускорения на единичный касательный вектор траектории — можно выразить так:

Нормальное ускорение (центростремительное ускорение) — ускорение, направленное перпендикулярно мгновенной скорости и изменяющее ее по направлению Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

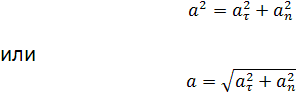
Направление полного ускорения также определяется правилом сложения векторов:

3 угловая скорость и угловое ускорение материальной точки и их связь с линейной скоростью и ускорением. Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные), остаются во все время движения неподвижными (рис.13). Угловой скоростью называется векторная величина, равная первой производной угла поворота тела по времени:

Вектор ω направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор dφ (рис. 2). Размерность угловой скорости dim ω = Т-1, а ее единица — радиан в секунду (рад/с). Если ( = const, то вращение равномерное и его можно характеризовать периодом вращения T ≈ временем, за которое точка совершает один полный оборот, т.е. поворачивается на угол 2p. Так как промежутку времени Dt = T соответствует ═= 2p, то ═= 2p/T, Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называется частотой вращения ОТКУДА

Угловым ускорением называется векторная величина, равная первой производной угловой скорости по времени: При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ═сонаправлен вектору ═(рис.8), при замедлен╜ном ≈ противонаправлен ему

связь между линейными (длина пути s, пройденного точкой по дуге окружности радиуса R, линейная скорость v, тангенциальное ускорение , нормальное ускорение ) и угловыми величинами (угол поворота j, угловая скорость w, угловое ускорение e) выражается следующими формулами: В случае равнопеременного движения точки по окружности (e=const) где═ w0 ≈ начальная угловая скорость.