1.2.2 Аналитический метод решения (метод Фурье)

Классическим методом решения уравнения

(1.3)

является метод разделения переменных (метод Фурье). Основой которого является предположение, что решение можно представить в виде произведения двух функций, одна из которых является функцией безразмерных координат, а другая — функцией только критерия F₀. Таким образом, находятся частные решения уравнения n Θ , удовлетворяющие граничным условиям, но не удовлетворяющие начальным. Затем, пользуясь линейностью уравнения, находят решение как линейную суперпозицию этих частных решений:

(1.4)

которая удовлетворяет уже начальным условиям путем соответствующего выбора коэффициентов n A . Θ представляется в виде:

Θ(x, y, z, Bi, Fo) = (x, y, z, Bi) ψ (Fo) (1.5)

Подстановка (.1.5) в уравнение (1.3) дает:

или (1.6)

отсюда,

(1.7)

Равенство (1.6) возможно лишь в том случае, если левые и правые его части — одинаковые постоянные величины, не зависящие ни от времени, ни от координат. Обозначим эту константу через - «т» (знак минус принят для удобства последующих преобразований, что отнюдь не налагает каких-либо ограничений на знак самой константы т).

Тогда исходная задача сводится к следующим двум:

1. ; (1.8)

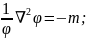
2. (1.9)

Решение обыкновенного дифференциального уравнения (1.8) имеет вид

ψ = Aexp(−mFo) , (1.10)

где А — произвольная константа [3].

1.3Влияние пористости вещества на процессы охлаждения

В работе [5] установлено что, пористость веществ оказывает существенное влияние на процессы теплообмена (так называемое пористое охлаждение) за счет активного взаимодействия охладителя с набегающим потоком газа, уменьшается тепловой поток к поверхности, но внешний контур поверхности тела не изменяется во времени, как бы долго ни продолжалось тепловое воздействие. Механизм пористого охлаждения складывается
в общем из двух процессов: внутреннего теплообмена, во время которого газ отбирает тепло от пористой стенки при фильтрации к внешней поверхности, и внешнего теплообмена, когда охлаждающий
газ, покинув стенку, диффундирует через пограничный слой, разбавляя и оттесняя от поверхности высокотемпературный газовый поток, что обеспечивает более высокую эффективность пористого охлаждения по сравнению с системами накопления тепла.

Пористая среда - твердое тело, содержащее пустые
промежутки (поры), распределенные более или менее равномерно по объему тела. Основной характеристикой такой среды является пористость. Объемная пористость материала П
обычно определяется как отношение объема пор V_п
к объему тела V₀.

П= V_п/ V₀. (1.11)

Поскольку остальная часть V_Т общего объема материала занята частицами твердого каркаса, то отсюда следует:

1-П= V_т/ V₀. (1.12)

В частности, для пористых материалов с каркасом из сферических
частиц диаметром d пористость можно определить из

, (1.13)

где N— число частиц в единице объема.

Существует ряд экспериментальных методик и приборов для определения пористости различных материалов.

Под структурой пористого тела понимают геометрическое строение
твердого каркаса, характеризуемое взаимным расположением его элементов. Для описания структуры пористых тел используются, упрощенные модели, в основе которых лежит либо представление о порах тела как о капиллярных цилиндрических трубах, либо пористое тело рассматривается как система сферических частиц, которые могут
быть и пустотелыми. При этом указанные частицы могут иметь различное пространственное расположение. Известно, что наибольшая пористость достигается при использовании одинаковых по размеру сферических зерен. В качестве простейших
форм укладки можно привести кубическую или ромбическую [5,6].

От вида укладки и геометрии частиц зависит величина и форма капилляров между ними. Пористость среды, состоящей из сферических частиц одинакового диаметра определяется только видом укладки. Кубическая укладка (рис.1.1, а) характеризуется пористостью 0,476, а при
наиболее плотной — ромбической упаковке (рис. 1.1,б) пористость снижается до 0,259. Это значение соответствует теоретически минимальной
пористости при упаковке сфер без их деформации. Однако в реальных материалах эти коэффициенты увеличиваются, так как в материалах имеются зерна различных размеров. Также принятая в теории форма пор очень проста, и значительно отличается от тех, которые образуются при получении пористых материалов [3,7].

Рисунок 1.1 - Модели структуры пористых материалов

Для обеспечения механической прочности в состав пористых материалов вводят более легкоплавкие волокна, и равномерно распределяют их в смеси. При таком способе связь между разнородными волокнами образуется за счет плавления в процессе обжига более легкоплавкого стеклянного волокна (температура дилатометрического размягчения 500-700°С) и растекания его по поверхности тугоплавких волокон, что обеспечивает их жесткое соединение в композиционном материале.

Как правило пористые материалы обладают развитой внутренней поверхностью, за счет мелкозернистой структуры материалов, удельная внутренняя поверхность больше, чем у материалов с крупнозернистой структурой. Внутренняя поверхность сферических частиц у спрессованных материалов рассчитывается по формуле:

f=Nπd=6(1-П)/d (1.14)

Величина удельной поверхности играет важную роль при расчете
теплообмена между твердым каркасом и охлаждающим веществом.