2.2.1. Выбор желаемого характеристического уравнения.
Характеристическое уравнение, а точнее расположение корней характеристического уравнения определяет динамику процесса, т. е. обеспечивает определенные показатели качества управления. На практике наибольшее распространение получили следующие характеристические полиномы:
стандартная биномиальная форма характеристического полинома;
стандартная форма характеристического полинома, настроенная на фильтр Боттерворта;
стандартная биномиальная форма характеристического полинома, настроенная на минимум квадратичной интегральной ошибки.
2.2.1.1.Стандартная биномиальная форма характеристического полинома
Стандартная биномиальная форма характеристического полинома имеет вид:
(60)
Корни
этого характеристического полинома
являются отрицательными действительными
и равными друг другу
.
А это означает что переходный процесс
будет носить апериодический характер
(перерегулирование σ%=
0) с временем переходного процесса
.
То есть корень характеристического
уравнения
является степенью
быстродействия
системы.
Характеристические
уравнения для
:
(61)
Переходные процессы, соответствующие данным характеристическим уравнениям представлены на рисунке:
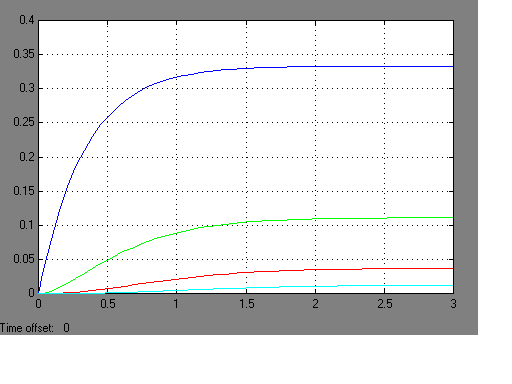
Рис. 2.21.
Несмотря на отсутствия перерегулирования, такие переходные процессы при исследовании электромеханических систем не всегда удовлетворяют по быстродействию.
2.2.1.2. Стандартная форма характеристического полинома, настроенная на фильтр Боттерворта
Фильтр Боттерворта имеет амплитудно-частотную характеристику, близкую по форме к прямоугольной характеристике идеального фильтра,:
(62)
Корни характеристического полинома, настроенные на фильтр Боттерворта располагаются на дуге окружности с радиусом , т. е. в общем случае являются комплексными корнями с отрицательными действительными частями. А это означает, что переходный процесс будет с перерегулированием.
Характеристические уравнения для :
Рис. 2.22.
Рис. 2.23.
Рис.2.24.
Переходные процессы, соответствующие данным характеристическим уравнениям представлены на рисунке:
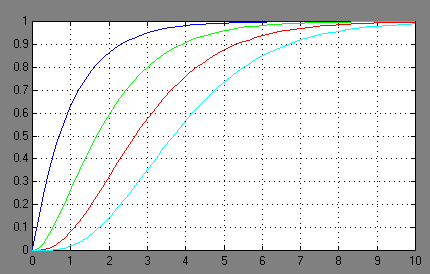
Рис. 2.26.
Переходные процессы имеют перерегулирование:
(63)
Быстродействие системы выше , чем в биномиальном случае.
Несмотря на отсутствия перерегулирования, такие переходные процессы при исследовании электромеханических систем не всегда удовлетворяют по быстродействию.
2.2.1.3. Стандартная форма характеристического полинома, настроенная на минимум квадратичной интегральной оценки.
Квадратичная интегральная оценка предусматривает настройку системы по пере5ходному процессу в целом по следующему принципу:
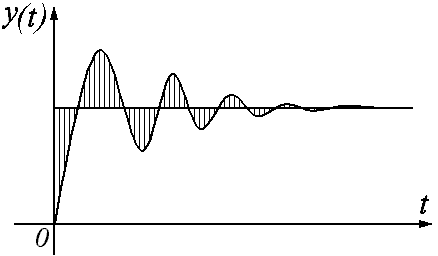
Рис. 2.27.
(64)
Исходя из этих правил, характеристические уравнения для имеют вид:
(65)
Корни характеристического полинома, настроенные на минимум квадратичной интегральной ошибки, тоже в общем случае являются комплексными корнями с отрицательными действительными частями.
Переходные процессы, соответствующие данным характеристическим уравнениям представлены на рисунке:
Рис. 2.28.
Такие системы, несмотря на минимум в целом квадратичной ошибки, являются более грубыми (σ%≈16%)
Пример:
Построить модальный регулятор для объекта (двигатель постоянного тока), обеспечивающим следующие показатели качества: σ%=0%, tпп=3с.:
Рис. 2.29.
Параметры
системы:
Схема переменных состояния
Рис. 2.30.
Описание в пространстве состояния:
Проверка системы на управляемость:
система
управляема
Проверка системы на наблюдаемость:
система
наблюдаема
Наблюдаемость и управляемость являются необходимыми условиями для синтеза.
Схема переменных состояния с модальным регулятором
-
Рис. 2.31.
Выбираем
желаемый характеристический полином
в стандартной биномиальной форме, что
обеспечивает σ%=0%
Результаты моделирования САУ с модальным регулятором:
Рис. 2.32.