Однозначность характеристики:

• Однозначные нелинейные элементы имеют характеристику, которая зависит не только от входного сигнала, но и от знака изменения входного сигнала.

• Неоднозначные нелинейные элементы имеют характеристику, которая зависит не только от входного воздействия, но и от знака изменения входного сигнала.

4.3. Типовые нелинейности

1. Идеальное реле

Рис. 4.8.

2. Трехпозиционное реле или реле с зоной нечувствительностью

Рис. 4.9.

3. Двухпозиционное реле с гистерезисом

Рис. 4.10.

4. Трехпозиционное реле с гистерезисом

Рис. 4.11.

5. Нелинейность типа насыщения

Рис.4.12.

6. Нелинейность типа насыщения с зоной нечувствительности

Рис. 4.13.

7. Усилитель с переменным коэффициентом усиления

Рис. 4.14.

8. Типа «идеальный диод»

Рис. 4.15.

9. Типа «модуль»

Рис. 4.16.

10. Типа «зазор»

Рис. 4.17.

11. Петля гистерезиса

Рис. 4.18.

4.4. Структурные преобразования нелинейных систем.

Структурные схемы нелинейных систем содержат линейные элементы и нелинейные элементы. Поскольку параметры нелинейных элементов зависят от величины входного сигнала и начальных условий, то в нелинейных системах не выполняется принцип суперпозиции и коммутативности, т. е. при структурных преобразованиях нелинейной системы в общем случае нельзя переносить узлы, сумматоры и звенья через нелинейные звенья. К линейным участкам схемы можно применять все правила преобразований. Нелинейные звенья, соединенные последовательно, параллельно и встречно-параллельно (с обратной связью) можно объединять в одно звено по следующим правилам.

1. Последовательное соединение двух нелинейных звеньев.

Рис. 4.19.

(4.5)

2. Параллельное соединение двух нелинейных звеньев.

Рис. 4.20.

(4.6)

Нелинейный элемент с обратной связью

Рис. 4.21.

(4.7)

Если нелинейная система содержит статический нелинейный элемент, то для таких систем возможны следующие структурные преобразования:

3. Перенос узла с входа на выход нелинейного элемента

Рис. 4.22.

4. Перенос узла с выхода на вход нелинейного элемента

Рис. 4.23.

4.4.1. Типовая структурная схема нелинейных систем.

Наиболее распространенная структурная схема нелинейной системы имеет вид:

Рис. 4.24.

где НЭ - нелинейный элемент;

ЛЧ – линейная часть

Рассмотрим уравнения этой системы, связывающее входной (r) и выходной (y) сигналы.

(4.8)

Уравнение, связывающее входной и выходной сигнал нелинейного элемента (x и y_Н) имеет вид:

(4.9)

ПРИМЕР

Пусть дана следующая нелинейная система :

Рис. 4.25.

Необходимо ее преобразовать к типовому виду (Рис. 4.24). Для этого осуществляется перенос первого сумматора на выход звена

Рис. 4.26.

Затем объединяются две ветви обратной связи

Рис. 4.27.

Далее система приводится к единичной обратной связи

Рис. 4.28.

Полученная нелинейная система отличается от типовой двумя дополнительными линейными звеньями: на входе и выходе системы. Линейное звено можно исключить из системы, заменив входной сигнал по формуле:

(4.10)

А зная сигнал , можно получить выходной сигнал системы по выражению:

(4.11)

Таким образом, для анализа свойств нелинейной системы можно ограничиться рассмотрением типовой схемы нелинейной системы (Рис. 4.24).

ПРИМЕР

Вывести уравнение, связывающее входной и выходной сигнал нелинейного элемента (x и y_Н)

Рис. 4.29.

Где , а нелинейный элемент – реле, имеющий статическую характеристику :

Рис. 4.30.

(4.12)

(4.13)

Если входной сигнал – единичное ступенчатое воздействие, то (4.13) принимает вид

(4.14)

4.5. Исследование нелинейных систем.

При анализе нелинейных систем обычно решают следующие задачи:

• Решение задачи устойчивости нелинейных систем, которая сводится к определению: устойчивости в целом (или абсолютной устойчивости); устойчивости в малом и устойчивости в большом.

• Определение возможности возникновения автоколебания: определение параметров системы, при которых они возникают; определение параметров автоколебаний (амплитуды, частоты).

Как отмечалось выше, что режим автоколебаний является наиболее неблагоприятным, поэтому задача определения возможности автоколебаний в нелинейных системах является первоочередной.

Исследование режима автоколебания.

Для исследования режима автоколебаний существует несколько методов, Самые распространенные методы – это метод фазовых траекторий и метод гармонический линеаризации.

4.5.1. Метод фазовых траекторий.

Метод фазовых траекторий представляет собой графо-аналитический способ исследования нелинейных систем. Сущность метода заключается в описании поведения системы при помощи наглядных геометрических представлений – фазовых портретов.

Динамика нелинейных систем с выходной переменной в общем случае описывается с помощью нелинейного дифференциального уравнения:

(4.15)

Данное уравнение можно представить в виде системы нелинейных дифференциальных уравнений первого порядка:

(4.16)

Переменные называются фазовыми переменными состояния. Мгновенное состояние системы и ее дальнейшее поведение однозначно определено, если в некоторый момент времени известны значения всех переменных . Эти значения можно рассматривать как координаты точек в n-мерном пространстве, которое называется фазовым пространством.

Точку с координатами называют изображающей точкой, а линию, по которой она перемещается при изменении состояния системы – фазовой траекторией. Известно, что конкретному начальному состоянию системы соответствует единственное решение системы (4.16), а следовательно единственная фазовая траектория. Поэтому множеству различных начальных условий соответствует семейство фазовых траекторий, которое называется фазовым портретом. Построение фазового портрета дает нагляднее представление о поведении системы, в том числе предоставляет возможность определить режим автоколебаний.

Метод фазового пространства наиболее удобен для анализа систем второго порядка, так как их фазовые траектории располагаются в одной плоскости – в фазовой плоскости переменных x₁ и x₂. Фазовый портрет этих систем можно построить непосредственно по дифференциальному уравнению, не решая его.

Пусть описание системы представлено в виде дифференциального уравнения второго порядка:

(4.17)

Данное уравнение можно представить в виде системы двух дифференциальных уравнений первого порядка

, (4.18)

где - отклонение выходной величины от установившегося значения. В качестве переменной принята производная переменной : . Разделив второе уравнение системы (4.18) на первое, можно получить уравнение фазовых траекторий в дифференциальной форме:

(4.19)

Решение данного дифференциального уравнения имеет уравнения фазовых траекторий в явном виде:

, (4.20)

где - постоянная интегрирования, зависящая от начальных условий.

ПРИМЕР

Рассмотрим колебательное звено (систему второго порядка):

(4.21)

Вывести уравнение фазовой траектории.

Дифференциальное уравнение, соответствующее данному звену имеет вид:

(4.22)

Данное дифференциальное уравнение может быть представлено в виде системы уравнений:

, (4.23)

где

Разделив второе уравнение системы на первое, получаем уравнение фазовых траекторий в дифференциальной форме:

(4.24)

Метод фазовых траекторий удобно применять, если объект управления описание в терминах пространства состояния.

4.5.1.1. Применение метода фазовых траекторий для системы описанной в терминах пространства состояний.

Рассмотрим применение метода фазовых траекторий на примере колебательного звена.

Передаточная функция колебательного звена может быть преобразована к следующему виду:

(4.25)

Схема переменных состояния имеет вид

Рис. 4.31.

(4.26)

Нетрудно заметить, что переменные фазового пространства совпадают с динамичекими переменными простанства состояния , что позволяет не только упростить процедуру получения уравнения фазовой траектории, но и получить фазовые траектории системы без решения уравнения фазовой траектории путем моделирования объекта, представленного в виде схемы переменных состяния.

Рассмотрим метод фазовых траекторий применительно к линейным системам.

4.5.1.2. Метод фазовых траекторий для линейных систем.

Как известно, в линейных системах второго порядка возможны следующие переходные процессы:

1. Устойчивые:

   1. колебательный;

   2. апериодический.

2. Неустойчивые:

   1. колебательный;

   2. апериодический.

3. Переходные процессы системы, находящейся на границе устойчивости:

   1. апериодическая граница устойчивости;

   2. колебательная граница устойчивости.

Рассмотрим эти переходные процессы и фазовые траектории, соответствующие данным переходным процессам

Устойчивый колебательный переходный процесс имеет вид:

Рис. 4.32.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.33.

Устойчивый апериодический переходный процесс имеет вид:

Рис. 4.34.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.35.

Неустойчивый колебательный переходный процесс имеет вид:

Рис. 4.36.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.37.

Неустойчивый апериодический переходный процесс имеет вид:

Рис. 4.38.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.39.

Система, находящаяся на границе колебательной устойчивости, имеет переходный процесс:

Рис. 4.40.

Фазовая траектория для данного переходного процесса имеет вид:

Рис. 4.41.

Рассмотрев фазовые траектории для линейных систем можно сделать следующие выводы:

• В верхних квадрантах фазовой плоскости изображающая точка движется всегда слева направо, а в нижних – справа налево. Это объясняется тем, что при переменная возрастает, а при переменная убывает.

• В любой точке фазовой плоскости, где переменная и функция не равны нулю, фазовая траектория имеет только одно определенное направление, соответствующее значению производной в данной точке. Из этого следует, что фазовые траектории в таких точках не пересекаются.

• Если , то , т. е. фазовые траектории пересекают ось под прямым углом, а переменная достигает своего максимума. Если при одновременно , то фазовая траектория в таких точках не имеет определенного направления, а обе производные и равны нулю. (18). Последнее означает, что изображающая точка неподвижна, а исследуемая система управления находится в состоянии равновесия. Такие точки называются особыми.

• Если переходный процесс является сходящимся, что соответствует устойчивым система, то фазовая траектория имеет вид либо скручивающейся к началу координат спирали (для колебательного процесса), либо дуги, сходящейся к началу координат (для апериодического процесса);

• Если система неустойчива, то фазовая траектория - раскручивающаяся спираль или расходящаяся дуга;

• Если в системе установились колебания с постоянной амплитудой и частотой, то фазовой траекторией является эллипс, который называется предельным циклом.. По параметрам эллипса можно определить амплитуду и частоту;

• Для всех фазовых траекторий характерны следующие особенности: в верхних квадрантах плоскости фазовые траектории имеют направление слева направо; в нижнем квадранте – справа налево

Свойства фазовых траекторий для линейных систем сохраняются и для фазовых траекторий нелинейных систем. Однако фазовые траектории нелинейных систем имеют свои особенности.

4.5.1.3. Особенности нелинейных систем:

• В нелинейных системах, как правило, рассматривают фазовый портрет системы, т. е. совокупность фазовых траекторий, соответствующих различным начальным условиям.

• Нелинейные элементы изменяют фазовые траектории, например фазовые траектории нелинейных систем с нелинейностями типа «реле» имеют изломы в линии, называемой линией переключения

Рис. 4.42.

• Если нелинейный элемент имеет зону нечувствительности, то фазовый портрет нелинейной системы имеет множество особых точек, которые определяют отрезок равновесия.

Рис. 4.43.

• Режиму автоколебаний соответствует фазовый портрет, на которм фазовые траектории сходятся к предельному циклу.

Рис. 4.44.

• Для систем устойчивых в малом, но неустойчивых в большом фазовый портрет имеет вид, при котором фазовые траектории, внутри предельного цикла сходятся к началу координат, а вне предельного цикла расходятся от предельного цикла. Предельный цикл в данном случае является неустойчивым.

Рис. 4.45.

Метод фазовых траекторий графическим методом дает наглядное изображение устойчивости систем и определения режима автоколебания.

В отличие от линейных систем в нелинейных может быть несколько режимов автоколебания, что соответствует нескольким предельным циклам. Параметры предельного цикла определяют параметры автоколебания (амплитуду и частоту ). Однако метод фазовых траекторий удобен для исследования систем второго и третьего порядков, поэтому этот метод имеет ограниченное использование.

ПРИМЕР

Построить фазовый портрет для следующей системы

Рис. 4.46.

Где , а нелинейный элемент – реле, имеющий статическую характеристику :

Рис. 4.47.

Уравнение (4.12) можно переписать в виде

(4.27)

Если входной сигнал – единичное ступенчатое воздействие, то (27) принимает вид

(4.28)

Введем новые фазовые переменные:

(4.29)

Уравнение фазовых траекторий имеет вид:

(4.30)

При уравнение имеет вид:

(4.31)

При уравнение имеет вид:

(4.32)

Разрешив такие уравнения при заданных начальных условиях можно получить уравнение для фазовых траекторий:

Для

(4.33)

Для

(4.33)

4.5.2. Метод гармонической линеаризации.

Метод гармонической линеаризации является приближенным методом исследования режима автоколебаний нелинейных систем. Этим методом можно определить условия возникновения и параметры автоколебаний как в системах второго порядка, так и в более сложных системах.

Метод основан на замене существенно нелинейного элемента системы эквивалентным линейным звеном. В замкнутой автоматической системе, работающей в режиме автоколебаний. Условием эквивалентности служит равенство амплитуд и фаз выходного сигнала эквивалентного звена и первой гармоники выходного сигнала реального нелинейного элемента. При этом предполагается, что сигнал на входе нелинейного элемента является синусоидальным. Такое предположение справедливо во всех случаях, когда линейная часть системы достаточно инерционна и не пропускает высокочастотные гармоники.

Рассмотри м типовую нелинейную систему

Рис. 4.48.

Если система находится в режиме автоколебаний, то на входе в нелинейный элемент сигнал является синусоидой:

(4.34)

На выходе нелинейного элемента сигнал имеет вид периодического сигнала, в общем случае отличного от синусоидального. Уравнение такого сигнала имеет вид:

(4.35)

Известно, что любой периодический сигнал может быть разложен в ряд Фурье и тем самым представлен в виде суммы гармонических составляющих:

(4.36)

где , - коэффициенты ряда Фурье определяются по формулам :

(4.37)

(4.38)

где Т – период повторения сигнала.

Однако уравнения (4.36) можно упростить, если учитывать следующее:

1. Статические характеристики большинства нелинейных элементов являются кососимметричными, т.е. симметричными относительно начала координат ( ). В этом случае постоянная составляющая и коэффициенты всех четных гармоник равны нулю( ).

2. Линейная часть нелинейных систем, которая располагается за нелинейным элементом, выполняет роль фильтра низких частот, т.е. на выходе нелинейной системы гасятся все гармоники кроме первой.

(4.39)

3,5....

На основе этих предпосылок уравнение (4.36) приобретает вид:

(4.40)

Из уравнения (4.34) можно получить:

(4.41)

(4.42)

(4.43)

Тогда уравнение (4.40) имеет вид:

(4.44)

Введем обозначения:

(4.45)

С учетом (4.45) уравнение (4.44) имеет вид:

(4.46)

или в операторном виде:

(4.47)

Таким образом, при выполнении указанных выше допущений нелинейное уравнение (4.35) может быть заменено линейным уравнением (4.46)или (4.47). Эта операция называется гармонической линеаризацией , уравнение (4.46) –уравнением гармонической линеаризации, а коэффициенты - коэффициентами гармонической линеаризации. Коэффициенты гармонической линеаризации зависят от вида нелинейной характеристики и могут быть определены по формулам (4.37), (4.38), (4.45).

Коэффициенты наиболее часто встречающихся нелинейных элементов приведены в таблице.*

Значения коэффициентов гармонической линеаризации.

Гармоническая линеаризация принципиально отличается от обычной линеаризации. При гармонической линеаризации:

• коэффициенты гармонической линеаризации и не являются постоянными, а зависят от амплитуды входного сигнала .

• Уравнение гармонической линеаризации содержит две составляющие: входной сигнал и его производную.

4.5.2.1. Применение метода гармонической линеаризации для определения режима автоколебаний.

Применяя гармоническую линеаризацию на вышеприведенных допущениях можно исследовать устойчивость системы методами теории устойчивости линейных систем.

Рассмотрим типовую нелинейную систему. Передаточная функция линейной части имеет вид:

(4.48)

Эквивалентную передаточную функцию нелинейного элемента можно получит из (47):

(4.49)

Тогда передаточная функция замкнутой системы имеет вид:

(4.50)

А характеристическое уравнение гармонически линеаризованной системы имеет вид:

(4.51)

Наиболее удобно исследовать автоколебания при помощи критерия Михайлова:

(4.52)

Согласно критерию устойчивости Михайлова в системе установятся колебания с постоянной амплитудой и частотой , если годограф Михайлова проходит через начало координат, т. е. когда и мнимая и действительная части характеристического полинома одновременно равны нулю:

(4.53)

Разрешая данную систему уравнений относительно , можно определить возможность возникновения автоколебаний в системе. Если уравнения (4.53) не имеют положительных корней , то автоколебания в системе невозможны.

Если положительные величины, то системе возможен режим колебания с постоянной амплитудой. Определить, являются ли данные колебания автоколебаниями, можно с помощью дополнительных исследований.

Изучая фазовые траектории, соответствующие режиму автоколебаний, можно сделать следующий вывод: что в режиме автоколебаний при увеличении амплитуды на величину в системе происходил сходящийся процесс к величине ; а при уменьшении на происходил расходящийся процесс до величины . Аналогичные процессы происходят при изменении частоты .

Для дополнительных исследований на устойчивость колебаний применяются критерии устойчивости: Гурвица, Михайлова и Найквиста.

4.5.2.2. Критерий Гурвица для определения режима автоколебания.

Для того чтобы колебания были устойчивыми по Гурвицу необходимо выполнение следующих условий:

• предпоследний определитель матрицы Гурвица должен быть равен нулю:

(4.54)

• все определители Гурвица, для характеристического уравнения нелинейной системы после гармонической линеаризации при увеличении амплитуды входного сигнала, должны оставаться положительными:

(4.55)

• все определители Гурвица, кроме двух последних, при уменьшении амплитуды входного сигнала должны быть отрицательными:

(4.56)

Аналогично критерий Гурвица применяется и для частоты .

4.5.2.3. Критерий Михайлова для определения режима автоколебания.

По критерию Михайлова выполнение нижеприведенного неравенства означает возможность режима автоколебаний:

>0 (4.57)

Если линейная часть описывается уравнением высокого порядка или содержит звено чистого запаздывания, то применение критерия становится затруднительным, и тогда применяют критерий Найквиста.

4.5.2.4. Критерий Найквиста.

Согласно критерию Найквиста система находится на колебательной границе устойчивости, если амплитудно-фазовая характеристика разомкнутого контура проходит через точку . Следовательно, условием существования автоколебаний является равенство:

(4.58)

или

(4.59)

Левая часть уравнения (4.59) представляет собой АФХ линейной части, а правя – обратную характеристику нелинейного элемента, взятую с противоположным знаком.

Уравнение (4.59) можно решить графически. Строится два графика , точки пересечения этих графиков определяют режимы колебаний с постоянной амплитудой и частотой.

Для определения режима автоколебаний пользуются следующим правилом:

Если точка на графике , близкая к точке пересечения, но сдвинутая в сторону увеличения параметра не охватывается графиком , то колебания являются устойчивыми, в противном случае – неустойчивыми.

Рис. 4.49.

На рисунке точка М₁ соответствуют режиму автоколебаний, а М₂ – неустойчивым колебаниям.

ПРИМЕР

Пусть дана нелинейная система:

Рис. 4.50.

Параметры системы:

Линейная часть представлена , где k=0.4; T₁=1 c; T₂=5 c.

Нелинейный элемент имеет характеристику

Рис. 4.51.

Определить есть ли в данной системе автоколебания. Если есть, то найти параметры входного воздействия, при котором в системе наблюдаются автоколебания.

Применим метод гармонической линеаризации:

Найдем значение x_m, ω.:

Из второго уравнения системы имеем:

=>

В системе возможны автоколебания при ω>0, значит, они возможны только при

Из первого уравнения системы найдем x_m, соответствующие

Разрешив биквадратное уравнение через замену переменной

Получаем четыре корня:

Очевидно, что при всех x_m ограничения (1), (2) выполняются, при x_m ≤0 в системе автоколебаний быть не может. Получилось 2 решения системы: (0.45;1.001) и (0.45;21.253). Для дополнительных исследований используем критерий Михайлова:

Проверим, выполняется ли неравенство (*) для полученных решений:

а). При ω=0.45 x_m=1.001

Как видно неравенство не выполняется, значит, при данных значениях в системе автоколебаний не будет.

б). При ω=0.45 x_m=21.253

Неравенство выполняется, значит, при данных значениях входного сигнала в системе будут наблюдаться автоколебания. Промоделируем эту схему в MATLAB 5.1.

Полученная схема:

Рис. 4.52.

Выходной сигнал системы при значениях входного сигнала ω=0.45 x_m=21.253:

Рис. 4.53.

Фазовая траектория:

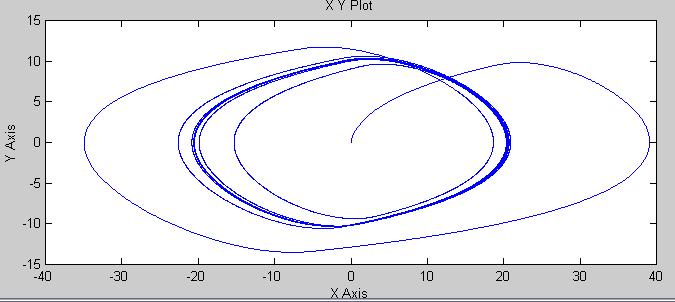
Рис. 4.54.

4.6. Оценка абсолютной устойчивости нелинейных систем по критерию Попова.

Критерий абсолютной устойчивости Попова дает достаточное условие абсолютной устойчивости нелинейной системы с одной однозначной нелинейностью.

Критерий Попова основан, как и критерий Найквиста, на использовании амплитудно-фазовой характеристики и имеет простую геометрическую интерпретацию.

Пусть в контуре нелинейной системы содержится нелинейный элемент с характеристикой , имеющей любую конфигурацию, но не выходящей за пределы определенного сектора [0, k_H]

Рис. 4.55.

Линейная часть имеет амплитудно-фазовую характеристику:

(4.60)

На основе данной характеристики строится модифицированная амплитудно-фазовая характеристика:

, (4.61)

где - коэффициент масштабирования (обычно берется равным единице).

Тогда критерий Попова формулируется следующим образом:

Для абсолютной устойчивости нелинейных систем одного класса, характеризующихся прямой с наклоном К_Н, достаточно чтобы модифицированная АФХ не охватывала точку (-1/К_н;j0) и через эту точку можно было бы провести прямую так, чтобы модифицированная амплитудно-фазовая характеристика не пересекала эту кривую и осталась справа.

Рис. 4.56.

Рис. 4.57.

Рис. 4.58.

Нетрудно заметить, что в соответствии с критерием Попова система (Рис. 4. 56) абсолютно устойчива, а системы (Рис. 4.57, 4.58) не являются абсолютно устойчивыми.

Критерий Попова может быть использован и при обратной задаче - выборе нелинейных элементов в нелинейной системе. В данном случае выбор нелинейного элемента не должен влиять на устойчивость системы.

Данная задача решается следующим образом: строится модифицированная амплитудно-фазовая характеристика и проводится прямая наиболее близкая к этой характеристике. Точка пересечения этой прямой с осью абсцисс определяет коэффициент наклона К_н, а значит и класс нелинейных характеристик.

ПРИМЕР

Пусть дана нелинейная система. Линейная часть представлена передаточной функцией с параметрами . Нелинейный элемент - двухпозиционное реле с параметрами . Определить является ли данная система абсолютно устойчивой.

Определим коэффициент наклона

Построив модифицированную амплитудно-фазовую характеристику, нетрудно, что МАФХ пересекает ось абсцисс в точке (-0,11;j0) и что через точку (-0,125;j0) можно провести прямую, не пересекающую модифицированную амплитудно-фазовую характеристику (Рис. 4.59).

Рис. 4.59

Определим допустимое значение параметра , при котором система абсолютно устойчива.

МАФХ пересекает ось абсцисс в точке (-0,11;j0). Следовательно, критическое значение параметра определится следующим образом:

То есть при параметре система не будет абсолютна устойчива.

4.7. Метод припасовывания.

Этот метод применяется для нелинейных систем управления, нелинейные элементы которых имеют кусочно-линейную или кусочно постоянную статическую характеристику.

Отрезки кусочно-линейной характеристики определяют количество участков, которые и участвуют в процедуре припасовывания. Метод припасовывания является точным методом решения конкретного уравнения, но трудоемок в вычислениях, которая возрастает с увеличением порядка линейной части и сложностью нелинейной характеристики.

Алгоритм метода припасовывания:

1. Составляются уравнения, описывающие нелинейную систему на каждом из участков нелинейной характеристики;

2. Для каждого из участков решаются в общем виде линейные уравнения;

3. По заданным начальным условиям и входному воздействию, определяется участок, с которого начинается переходный процесс. С учетом данных условий вычисляются произвольные постоянные, входящие в общее решение уравнения;

4. Решается уравнение для граничного значения данного участка линейной характеристики;

5. Повторяются п.3, 4.

Рис. 4.60

Рис. 4.61

(4.62)

(4.63)

I участок:

II участок:

III участок:

Начальные условия:

.

Пример:

Рис. 4.62

Рис. 4.63

Даны начальные условия:

Рассчитаем:

I :

II:

-общее решение, где С₁ и С₂ - константы.

И выражаем t_k.

4.8. Коррекция нелинейных систем

Коррекция нелинейных автоматических систем осуществляется обычно с целью обеспечения устойчивости систем или с целью получения автоколебаний. Коррекция может быть осуществлена изменением характеристик, как линейной части, так и нелинейного элемента.

Изменение характеристики нелинейной системы может быть получено различными способами:

• Компенсация статических нелинейных характеристик при помощи соответствующих обратных нелинейных характеристик.

• Построение корректирующих устройств по желаемой ЛАЧХ.

4.8.1. Компенсация статических нелинейных характеристик.

Компенсация статических нелинейных характеристик осуществляется путем включения в систему (последовательно или параллельно к нелинейному элементу) корректирующего устройства в виде нелинейного элемента с обратной нелинейной характеристикой

ПРИМЕР

Рассмотрим нелинейную систему следующего вида

Рис. 4.64

Переходные процессы на выходе системы и на выходе нелинейного звена имеют вид

Рис. 4.65

Рис. 4.66

Нелинейный элемент имеет характеристику

Если последовательно к нелинейному элементу включить корректирующее устройство в виде нелинейного элемента с характеристикой:

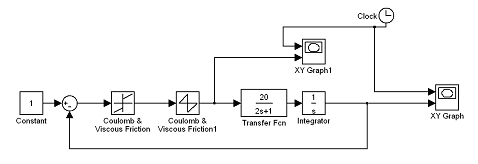
Рис. 4.67

Переходные процессы на выходе системы и на выходе нелинейного звена имеют вид

Рис. 4.68

Рис. 4.69

Аналогичные результаты получаются при параллельном соединении звеньев.

4.8.2. Построение корректирующих устройств по желаемой лачх.

В данном случае строится линейное корректирующее устройство по желаемой ЛАЧХ.

Рассмотрим следующую систему управления.

Рис. 4.70

Синтез последовательного корректирующего устройства осуществляется по следующему алгоритму;

1. Строится ЛАЧХ приведенной линейной части системы по передаточной функции :

, (4.64)

где - коэффициент усиления, выделенный из линейной функции

(4.65)

или

, (4.66)

где

- нормированный коэффициент гармонической линеаризации.

2. В соответствии с заданными показателями качества ( и σ%) строится желаемая ЛАЧХ так, как это делается для линейных систем.

3. Определяется ЛАЧХ последовательного корректирующего устройства :

(4.67)

4. По ЛАЧХ корректирующего устройства определяют передаточную функцию корректирующего устройства .

5. Строится ЛФЧХ φ(ω) скорректированной линейной части системы.

6. Строится запретная область, соответствующая допустимому показателю колебательности . ЛФЧХ скорректированной линейной части системы не должна заходить в запретную область. Если ЛФЧХ скорректированной линейной части системы заходит в эту область, то необходимо изменить параметры корректирующего устройства так, чтобы ЛФЧХ φ(ω) не заходила в эту зону, но при этом ЛАЧХ скорректированной части удовлетворяла заданным показателям качества.

7. Проводится моделирование системы.

Приведенная процедура синтеза отличается от процедуры синтеза линейных систем только пунктом построения запретной области.

4.8.2.1. Методика построения запретной области.

Передаточная функция разомкнутой системы гармонически линеаризованной системы с однозначной нелинейной характеристикой имеет вид:

(4.68)

Передаточная функция замкнутой системы определяется как :

(4.69)

Показатель колебательности для нелинейной системы определяется по формуле:

, (4.70)

где и - действительная и мнимая части АФХ приведенной линейной части системы ( ).

Преобразуя , получаем выражение:

(4.71)

Данное уравнение при является уравнением окружности. Пусть величина принимает значения в интервале:

(4.72)

Тогда по выражению можно построить семейство окружностей при при различных значениях из интервала. Линией одинакового значения является огибающая этого множества окружностей.

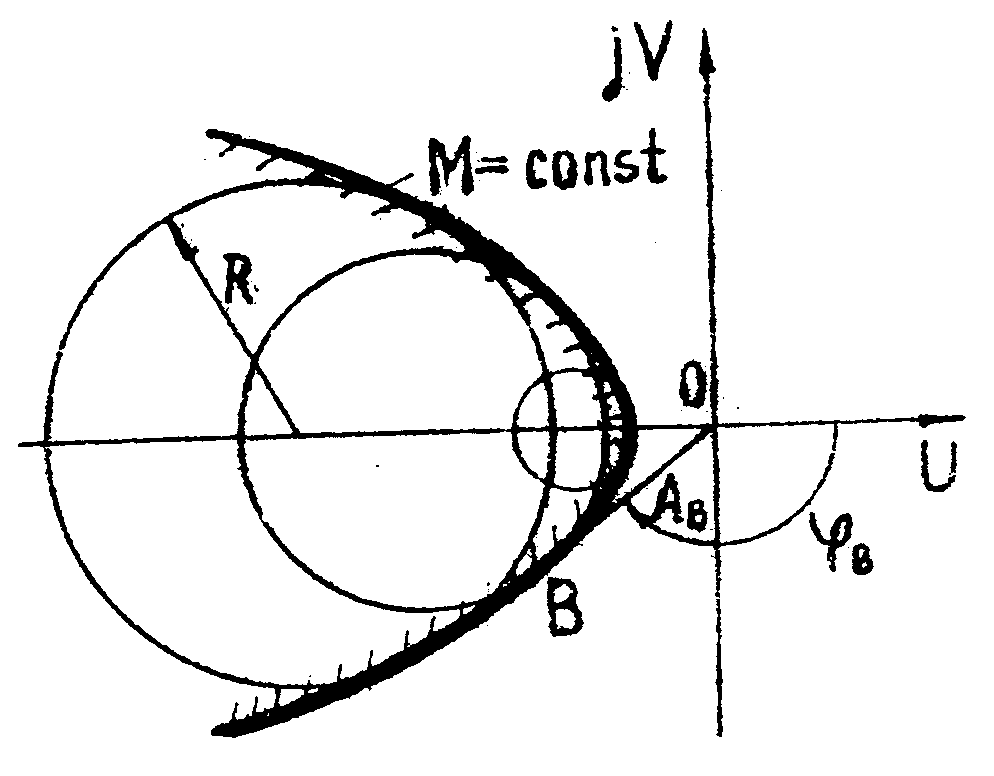
Рис. 4.71

Далее осуществляется перенос линии комплексной плоскости на плоскость ЛФЧХ. Данная линия и определяет запретную область для ЛФЧХ.

Рис. 4.72

5. Анализ и синтез систем при случайных воздействиях,

Во многих реальных системах автоматического управлении внешние воздействия (задающее и возмущающее) являются случайными величинами.

Рис. 5.1.

Пример: внешнее воздействие – момент сопротивления в добычных механизмах и буровых станках, нагрузки электрического генератора, питающего большое количество потребителей.

Иногда случайные воздействия создают в управляющем устройстве искусственно для улучшения процесса управления.

Все это вызывает необходимость при расчете использовать методы математической статистики.

Сущность статистического подхода к анализу и синтезу систем управления состоит в том, что при проектировании системы и при оценке ее качества ориентируются не на самые «тяжелые», но маловероятные условия, а на некоторые средние , наиболее часто встречающиеся условия.

5.1. Характеристики случайных сигналов

Случайной называется функция некоторой независимой переменной, значение которой при каждом данном значении независимой переменной является случайной величиной. Если независимая переменная - время, то случайная функция называется случайным (стохастическим или вероятностным) процессом.

Случайный процесс, в отличие от детерминированного, нельзя описать какой-либо определенной функцией времени . Случайный процесс представляет собой множество функций , обладающие некоторыми общими вероятностными свойствами.

Реализацией случайного процесса называется конкретная функция , которая получена в результате экспериментального наблюдения. Случайные процессы подразделяются на стационарные и нестационарные.

Стационарный случайный процесс - это процесс, статистические характеристики которого не изменяются во времени.

Нестационарный случайный процесс имеет статистические характеристики, которые с течением времени меняются.

Реальные системы, как правило, характеризуются стационарным случайным процессом.

Математический аппарат анализа стационарных случайных процессов основан на гипотезе эргодичности. Согласно гипотезе эргодичности статистические характеристики большого числа произвольно выбранных реализаций случайного стационарного процесса совпадают со статистическими характеристиками одной реализации достаточно большой длины. Это означает, что усреднение по множеству реализаций стационарного случайного процесса можно заменить усреднением по времени одной достаточно большой реализации. Тем самым существенно облегчается экспериментальное определение статистических характеристик стационарного случайного процесса и упрощается расчет систем при случайных воздействиях.

5.1.1 Основные статистические характеристики стационарного случайного процесса

На рис. 5.2 представлена реализация стационарного случайного процесса.

Рис. 5.2.

Определим основные статистические характеристики стационарного случайного процесса

Среднее значение сигнала на конечном интервале времени определяется как :

(5.1)

Если интервал достаточно бодьшой, то среднее значение определяет математическое ожидание

(5.2)

Если на практике конечная реализация представлена в виде дискретных значений, отделенных друг от друга равными промежутками времени , то среднее значение можно вычислить по формуле:

(5.3)

Стационарный случайный процесс можно рассматривать как сумму постоянной составляющей и переменной составляющей , соответствующей отклонениям случайного сигнала от среднего:

(5.4)

Сигнал называется центрированным случайным сигналом. Очевидно, сто среднее значение центрированного случайного сигнала равно нулю. Так как спектр реального сигнала совпадает со спектром центрированного случайного сигнала , то во многих ( но не во всех) задачах расчета автоматических систем можно вместо рассматривать сигнал .

Дисперсией называется среднее значение квадрата отклонений от математического ожидания :

(5.5)

- это мера разброса мгновенных значений сигнала около математического ожидания. Чем больше пульсация, тем больше

Средним квадратичным отклонением называется выражение вида:

(5.6)

Важным свойством статических характеристик является следующее:

(5.7)

Математическое ожидание и дисперсия являются важными характеристиками, но неисчерпывающими: по ним нельзя судить о скорости изменения сигнала во времени

Рис. 5.3.

Рис. 5.4.

На рисунках 5.3, 5.4 представлены стационарные случайные процессы, имеющие равные математические ожидания и дисперсии ( ). Однако из рисунков видно, что изменяется медленнее, чем . Интенсивность изменения стационарного случайного процесса во времени характеризуется следующими функциями: корреляционной функцией и функцией спектральной плотности.

5.1.1.1. Корреляционная функция

Корреляционная (автокорреляционная) функция - это математическое ожидание произведения мгновенных значений сигнала, разделенных промежутком времени :

(5.8)

Для центрированного сигнала корреляционная функция определяется по формуле:

(5.9)

где - варьируемый сдвиг по времени:

(5.10)

Фиксированному соответствует определенное числовое значение .

Корреляционная функция характеризует степень корреляции (связи) между предыдущими и последующими значениями сигнала.

Корреляционная функция обладает следующими свойствами:

1. При увеличении связь (корреляция) ослабевает.

2. Корреляционная функция убывает тем быстрее, чем быстрее изменяется случайный сигнал.

3. Корреляционная функция является четной функцией:

(5.11)

Экспериментально корреляционная функция определяют (вычисляют) по следующей схеме:

Рис. 5.5.

Если реализация представляет собой совокупность дискретных значений стационарного случайного процесса, зафиксированных через равные промежутки времени , то корреляционная функция определяется по формуле:

(5.12)

для получения достаточно достоверной информации о свойствах случайного процесса длину реализации и интервал следует выбирать из условий;

(5.13)

(5.14)

где и - периоды соответственно самой низкочастотной м высокочастотной составляющей сигнала.

5.1.1.2. Спектральная плотность

Функция не является периодической, поэтому она не может быть разложена в ряд Фурье. С другой стороны, функция из-за неограниченной длительности не интегрируема и поэтому не может быть представлена интегралом Фурье. Для избежания этих трудностей вводится вспомогательная функция , которая совпадает с функцией на интервале и равна нулю вне этого интервала :

(5.15)

Функция интегрируема и для нее существует прямое преобразование Фурье (интеграл Фурье):

(5.16)

Спектральной плотностью мощности случайного сигнала (или просто спектральной плотностью) называется функция вида:

(5.17)

Спектральная плотность - это функция, характеризующая распределение средних значений квадратов амплитуд гармоник сигнала. Спектральная плотность обладает следующими свойствами:

1. Чем быстрее изменяется стационарный случайный процесс, тем шире график .

2. Отдельные пики на графике спектральной плотности свидетельствуют о наличии у случайного сигнала периодических составляющих.

3. Спектральная плотность является четной функцией:

(5.18)

Спектральная плотность связана с дисперсией сигнала следующим соответствием:

(5.19)

Экспериментально спектральная плотность определяется (вычисляется) по следующей схеме:

Рис. 5.6.

Спектральная плотность связана с корреляционной функцией следующим выражением (по теореме Хинчина-Винера):

(5.20)

или

(5.21)

Если разложить множители и с помощью формулы Эйлера и учесть, что , и являются четными функциями, а - нечетная функция, то выражения (5.20), (5.21) можно преобразовать к следующему виду:

(5.22)

(5.23)

Выражения (5.23), (5.24) применяют в практических расчетах. Нетрудно заметить, что при выражение (5.24) определяет дисперсию стационарного случайного процесса.:

(5.24)

Соотношения, связывающие корреляционную функцию и спектральную плотность, обладают всеми присущими преобразованию Фурье свойствами и определяют следующие сравнительные характеристики: чем шире график , тем уже график , и наоборот , чем быстрее убывает функция , тем медленнее уменьшается функция . Эту взаимосвязь иллюстрируют графика на рис (5.7), (5.8)

Рис. 5.7.

Рис. 5.8.

Линии 1 на обоих рисунках соответствуют медленно меняющемуся случайному сигналу, в спектре которого преобладают низкочастотные гармоники. Линии 2 соответствуют быстроменяющемуся сигналу, в спектре которого преобладают высокочастотные гармоники.

Если случайный сигнал изменяется во времени очень резко и между его предыдущими и последующими значениями корреляция практически отсутствует, то корреляционная функция имеет вид дельта-функции (линия 3). График спектральной плотности в этом случае представляет горизонтальную прямую в диапазоне. Это указывает на то, что амплитуды гармоник во всем диапазоне частот одинаковы. Такой сигнал называется белым шумом (по аналогии с белым светом, у которого, как известно, интенсивность всех компонент одинакова).

Понятие «белого шума» является математической абстракцией. Физически сигналы в виде белого шума неосуществимы, так как бесконечно широкому спектру соответствует бесконечно большая дисперсия, а следовательно, бесконечно большая мощность. Однако часто реальные системы с конечным спектром можно приближенно рассматривать как белый шум. Это упрощение правомерно в тех случаях, когда спектр сигнала значительно шире полосы пропускания системы, на которую действует сигнал.

5.2. Типовые случайные воздействия

Реальные случайные воздействия, влияющие на промышленные объекты управления, разнообразны по своим свойствам. Но, прибегая к при математическом описании к некоторой идеализации, можно выделить ограниченное число типовых случайных воздействий:

1. Случайное воздействия типа «белый шум»;

2. Случайный ступенчатый сигнал;

3. Случайный сигнал, имеющий скрытую периодическую составляющую;

5.2.1. Случайное воздействия типа «белый шум»

Белый шум с ограниченной спектральной плотностью является простейшим типовым воздействием. Для него характерны резкие всплески и быстрые переходы от одного значения к другому (Рис. 5.9).

Рис. 5.9.

Спектральная плотность этого воздействия описывается функцией:

(5.25)

Рис. 5.10.

Дисперсия сигнала определяется как:

(5.26)

Корреляционная функция имеет вид:

(5.27)

Рис. 5.11.

Корреляционная функция можно определить через дисперсию сигнала:

(5.28)

5.2.2. Случайный ступенчатый сигнал

Случайный ступенчатый сигнал имеет вид:

Рис. 5.12.

У случайного ступенчатого сигнала случайными величинами являются моменты скачков и величины скачков.

Корреляционная функция этого сигнала имеет вид:

(5.29)

Рис. 5.13.

Спектральная плотность имеет вид:

(5.30)

Рис. 5.14.

Из графика видно, чем больше параметр , тем быстрее уменьшается корреляционная функция и тем шире график спектральной плотности. Ординаты функции при увеличении уменьшаются. При рассматриваемый сигнал приближается к идеальному белому шуму.

5.2.3. Случайный сигнал, имеющий скрытую периодическую составляющую

Часто случайный сигнал содержит периодическую составляющую

Рис. 5.15.

Такой сигнал имеет экспоненциальну0-косинусную корреляционную функцию:

(5.31)

Рис. 5.16.

Параметр этой функции соответствует среднему значению «периода» скрытой составляющей, а параметр. Если показатель мал и близок к значению , характеризует относительную интенсивность остальных случайных составляющих, которые наложены на периодическую составляющую. Если показатель мал и близок к значению , то относительный уровень этих составляющих невелик и смешанный сигнал близок к гармоническому.

Если показатель велик и равен , то уровень случайных составляющих соизмерим с «амплитудой» периодической составляющей. При корреляционная функция практически совпадает с корреляционной функцией случайного ступенчатого сигнала. экспонентой

Случайный сигнал, имеющий скрытую периодическую составляющую, имеет спектральную плотность:

(5.32)

Рис. 5.17.

Данная корреляционная функция имеет явно выраженный пик при

5.3. Преобразование случайного сигнала линейным звеном.

При воздействии стационарного случайного процесса на линейное устойчивое звено на выходе звена возникает также стационарный случайный процесс, который можно рассматривать как преобразованный входной сигнал.

Преобразование входного сигнала проявляется в изменении его статистических характеристик: математического ожидания, дисперсии, корреляционной функции и спектральной плотности.

Если входной сигнал – центрированный, то и выходной сигнал также будет центрированным. Далее рассматриваются центрированные сигналы (без обозначения их индексом в виде кружочка)

Для рассмотрения законов преобразования случайного сигнала вводятся характеристики, оценивающие связь между случайными сигналами: взаимнокорреляционная функция и взаимная спектральная плотность.

Взаимнокорреляционная функция стационарных случайных сигналов характеризует степень связи (корреляции) между мгновенными значениями сигналов и , отстоящих друг от друга на величину . Взаимнокорреляционная функция определяется по формуле:

(5.33)

Взаимнокорреляционная функция обладает следующими свойствами:

• Если сигналы и не связаны (не коррелированны) между собой, то при взаимнокорреляционная функция будет равна нулю при любых :

(5.34)

• Взаимнокорреляционная функция обладает свойством:

(5.35)

• Если случайный процесс представляет собой сумму двух случайных процессов:

, (5.36)

то взаимнокорреляционная функция имеет вид:

(5.37)

В этом случае взаимнокорреляционная функция называется автокорреляционной функцией.

Если сигналы и не связаны (не коррелированны) между собой, то взаимнокорреляционная функция (автокорреляционная функция) определяется как:

(5.38)

Взаимная спектральная плотность стационарных случайных сигналов и определяется следующим образом:

(5.39)

Взаимная спектральная плотность имеет следующие свойства:

• Взаимная спектральная плотность является комплексной функцией и для нее справедливо следующее:

, (5.40)

где * обозначены сопряженные функции.

• Если случайный процесс представляет собой сумму двух случайных процессов (5.36)

то взаимная спектральная плотность имеет вид:

(5.41)

Если сигналы и не связаны (не коррелированны) между собой, то взаимная спектральная плотность определяется как:

(5.42)

Рассмотрим связь между статистическими характеристиками двух стационарных случайных процессов и , являющимися входным и выходным сигналами линейной динамической системы с передаточной функцией .

Рис. 5.18.

Наиболее просто определяется связь между математическими ожиданиями этих сигналов. Так как у стационарных сигналов математические ожидания являются постоянными величинами, то связь между ними определяется уравнением статики звена:

(5.43)

Преобразование входного сигнала в выходной сигнал можно рассматривать во временной и частотной областях.

5.3.1. Преобразование сигнала во временной области

Выходной сигнал связан с входным сигналом :

, (5.44)

где - импульсная переходная характеристика звена, - переменная интегрирования.

Определим взаимнокорреляционную функцию сигналов и :

(5.45)

Таким образом, взаимнокорреляционная функция сигналов и определяется по формуле:

(5.46)

Так как интеграл (5.46) имеет такой же вид, как и (5.44), то функцию можно рассматривать как реакцию линейной системы на воздействие, имеющее форму корреляционной функции .

Определи корреляционную функцию :

(5.47)

Таким образом, корреляционная функция выходного сигнала определяется по формуле:

(5.48)

Выражение (5.48) показывает, что корреляционная функция выходного сигнала может быть получена двукратным взятием интеграла свертки от корреляционной функции входного сигнала.

Таким образом, преобразование линейной системы случайного входного сигнала в случайный выходной сигнал связано с корреляционными взаимнокорреляционной функциями и представлено .Рис. 5.19.

Рис. 5.19

Если на входе системы действует белый шум с корреляционной функцией (т. е. сигнал имеет неограниченную частотой пропускания спектральную плотность) , то взаимнокорреляционная функция и корреляционная функция выходного сигнала имеют выражения :

(5.49)

(5.50)

5.3.2. Преобразование сигнала в частотной области

Очевидно преобразование входного случайного сигнала линейной системой в частотной области (Рис. 5.20.) связано со спектральной и взаимной спектральной плотностями.

Рис. 5.20.

Найдем связь между спектральными плотностями сигналов и

(5.51)

Первый интеграл представляет собой передаточную функцию в частотной области , а второй спектральную плотность входного сигнала. Таким образом, взаимная спектральная плотность входного и выходного сигналов определяется:

(5.52)

или

(5.53)

Для спектральной плотности выходного сигнала справедливо следующее:

(5.54)

Заменяя первый и второй интегралы функциями и , а третий спектральной плотностью , получаем

(5.55)

или

(5.56)

Выражение (5.56) показывает, что спектральная плотность выходного сигнала равна спектральной плотности входного сигнала, умноженной на квадрат амплитудной частотной характеристики системы.

Фазовая характеристика системы не влияет на спектральную плотность выходного сигнала.

Таким образом, преобразование линейной системы случайного входного сигнала в случайный выходной сигнал в частотной области связано с спектральными и взаимной спектральной плотностями и может быть представлено в виде схемы (Рис. 5.21).

Рис. 5.21

Дисперсия выходного сигнала может быть определена по формуле:

(5.57)

Пример

Вычислить дисперсию на выходе апериодического звена, если на входе действует белый шум с ограниченной спектральной плотностью.

Дисперсия выходного согласно (57) имеет вид:

Из полученного выражения видно, что тем меньше, чем меньше интенсивность входного сигнала и чем больше постоянная времени

5.4. Минимизация дисперсии сигнала ошибки замкнутой системы

Рассмотрим линейную систему следующего вида:

Рис. 5.22

На систему действуют случайные возмущения и с известными спектральными плотностями и . Задающее воздействие также является случайным сигналом со спектральной плотностью . Пусть все три воздействия – центрированные сигналы. Тогда и сигнал ошибки тоже будет центрированным.

Если внешние воздействия не коррелированны между собой, то сигнал ошибки , возникающий в системе, может рассматриваться как сумма трех независимых составляющих:

(5.58)

Рис. 5.23

Составляющая обусловлена неточным воспроизведением задающего воздействия, а составляющие и - неполным подавлением возмущений и . Соответственно дисперсия сигнала ошибки будет определяться как:

(5.59)

Дисперсия случайного сигнала согласно (5.57) зависит от амплитудной частотной характеристики , которая определяется на основе передаточной функции

Передаточные функции , и могут быть вычислены по схемам:

Рис. 5.24

Рис. 5.25

Рис. 5.26

(5.60)

(5.61)

(5.62)

Каждая из дисперсий определяется по формулам:

(5.63)

(5.64)

(5.65)

При подстановке в формулы (5.63)-(5.65) конкретных значений и получаются довольно сложные выражения, интегрирование которых обычными методами затруднительно. Поэтому используют следующий прием. Подынтегральное выражение представляют в типовой форме – в виде отношения двух полиномов от переменной :

, (5.66)

где

(5.67)

Полином всегда имеет степень ниже и содержит только четные степени . Если в числителе окажутся нечетные степени, их можно отбросить.

В полиноме в виде сомножителя входит характеристическое уравнение замкнутой системы. Поэтому при приближении системы к границе устойчивости интеграл (5.66) резко возрастает.

Интегралы вида (5.66) для различных степеней вычислены заранее и приведены в справочниках по теории управления. Для степеней интегралы равны:

(5.68)

Представление интегралов (5.63)- (5.65) в форме (5.66) возможны практически для любой реальной системы, не содержащей запаздывание. Получив таким образом аналитическое значение дисперсии ошибки, получаем функцию от параметров системы:

, (5.69)

где - параметры системы. Минимизируя выражение (5.69) по параметрам и , можно определить их оптимальные значения.

Пример

Определить оптимальное значение передаточного коэффициента с передаточной функцией .

На входе системы действует задающее воздействие со спектральной плотностью .

На систему действует возмущение в виде белого шума с ограниченной спектральной плотностью для .

Внешнее воздействие отсутствует.

Таким образом, дисперсия сигнала ошибки определяется:

Дисперсия, обусловленная неточным воспроизведением задающего воздействия, имеет вид:

Сравнивая выражение с типовой формой записи интеграла (66), можно получить:

Окончательно дисперсия имеет вид:

нетрудно заметить, что чем больше коэффициент , тем меньше дисперсия , то есть тем точнее система воспроизводит на выходе задающее воздействие.

Дисперсия, обусловленная неполной компенсацией возмущения

У этого интеграла :

Окончательно дисперсия имеет вид:

Чем больше коэффициент , тем больше ошибка из-за прохождения возмущения на выход системы.

Суммарная дисперсия сигнала ошибки:

Оптимальное значение коэффициента усиления найдем из условия:

Откуда имеем:

оптимальное значение передаточного коэффициента системы зависит от соотношения уровней задающего и возмущающего воздействий.

6. Принципы построения оптимальных и адаптивных систем управления

6.1. Общая характеристика задач оптимального управления

Автоматическая система управления называется оптимальной, если она среди всех систем рассматриваемого класса осуществляет наилучшее в определенном смысле управление. Признак, по которому производятся сравнительная оценка возможных вариантов управления и выбор наилучшего варианта, называют критерием оптимальности.

В большинстве задач управления критерий оптимальности удается записать в математической форме в виде некоторой скалярной величины Q, которая при наилучшем варианте управления достигает экстремального значения (максимума или минимума):

Q = extremum. (6.1)

Критерий оптимальности (13.1) представляет собой математическую формулировку цели управления. Поэтому величину Q называют целевой функцией.

Физический смысл величины Q зависит от характера управляемого объекта и от конкретного назначения оптимизируемой системы. В качестве величины Q могут быть приняты различные технические и экономические показатели функционирования как самого объекта, так и всей системы в целом. Критерием оптимальности могут служить, например, максимум производительности технологической установки (экскаватора, добычного комбайна, дробилки и т. п.), максимум извлечения полезного компонента из обогащаемой руды, минимум затрат сырья или энергии на единицу продукции, минимум потерь полезного компонента в отходах, минимум длительности переходного процесса в системе управления, минимум отклонения стабилизируемой величины от ее заданного значения.

Приведенные примеры показывают, что все критерии можно объединить в две группы: функции выгоды, которые надо максимизировать, и функции потерь, которые необходимо минимизировать.

У многомерного объекта с несколькими входными и выходными переменными скалярная величина Q зависит в общем случае от вектора состояния х, а также от векторов задающего воздействия Х₃, управляющего воздействия у и возмущения z, т. е.

Q=Q(x, x₃, y, z). (6.2)

В зависимости от вида выражения (13.2) различают задачи статической и динамической оптимизации. Если компонентами векторов х, х₃, у, z являются установившиеся значения соответствующих переменных, то говорят о статической оптимизации (или оптимизации статического режима). Если же указанные переменные рассматриваются во времени, то приходится иметь дело с задачей динамической оптимизации (или оптимизацией динамического режима). При статической оптимизации величина Q является функцией нескольких скалярных переменных. В задачах динамической оптимизации экстремизируемая величина Q является функционалом — ее числовые значения определяются видом вектор-функций х(t), x₃(t), у(t), z(t):

Q = Q[x(t),x₃(t),y(t),z(t)]. (6.3)

Обычно функционал (13.3) представляет собой определенный интеграл, вычисляемый в интервале управления,

(6.4)

где F — скалярная функция, вид которой определяется целью управления.

Простейшими интегральными функционалами, зависящими от вида только одной скалярной функции, являются, например, интегральные оценки качества (см. 8.5).

Если целью управления является получение максимального быстродействия, то полагают F=1, и функционал (13.4) принимает тривиальный вид

(6.5)

Если при управлении одномерным объектом необходимо затратить минимум энергии на заданное его перемещение, то в функционал (13.4) входит квадрат управляющего воздействия

(6.6)

Статическую оптимизацию можно рассматривать как частный случай динамической оптимизации. Переход от динамической оптимизации к статической правомерен в тех случаях, когда скорость изменения внешних воздействий х₃ (t) и z (t) существенно меньше скорости свободного движения системы.

В общем случае математическая постановка задачи оптимального управления будет следующей.

Известно математическое описание объекта — например, в виде системы обыкновенных дифференциальных уравнений, записанной в векторной форме:

(6.7)

Требуется найти такой алгоритм управления

(6.8)

который обеспечивает экстремум (пусть для определенности минимум) величины Q:

Q=min. (6.9)

При этом должны быть соблюдены определенные ограничения на выходные переменные x₁, x₂,..., x_n и на управляющие воздействия y₁, y₂,...,y_k. Ограничения задаются обычно в виде неравенств:

(6.10)

(j=1; 2; ...; n; l=1; 2; ...; k),

где , — предельно допустимые значения соответствующих переменных (например, скорость движения подъемного сосуда, ток двигателя экскаватора и т. п.).

Такой постановке задачи оптимального управления соответствует обобщенная функциональная схема, приведенная на рис. 6.1.

В табл. 6.1 приведено словесное описание нескольких задач оптимального управления горно-технологическими объектами.

Задаче оптимального управления можно дать наглядную геометрическую интерпретацию в фазовом пространстве (рис. 6.2, а). Объект управления необходимо перевести из известного начального состояния, соответствующего точке х (0), в заданное состояние, характеризуемое точкой х (t_n). Это можно осуществить, как правило, по нескольким траекториям, соответствующим различным формам управляющей вектор-функции у (t). Причем при каждом варианте управления будет получаться свое значение величины Q. Оптимальному управляющему воздействию у*(t) и оптимальной траектории х*(t) соответствует, очевидно, экстремальное значение Q*.

Оптимальная траектория х*(t) обладает замечательным свойством: она оптимальна не только в целом — в интервале [0, t_п], но и каждый ее участок от любой промежуточной точки х(t_i) (рис. 6.2, б) до конечной точки х (t_n) также оптимален. Это положение было впервые сформулировано американским математиком Р. Беллманом в виде так называемого принципа оптимальности.

Принцип оптимальности означает, что оптимальное управление определяется лишь состоянием системы в текущий момент времени и не зависит от того, как система пришла в рассматриваемое текущее состояние. Так, если начальное состояние системы характеризуется точкой х (t_i) на общей оптимальной траектории

Рис. 6.1. Обобщенная функциональная схема автоматической системы оптимального управления

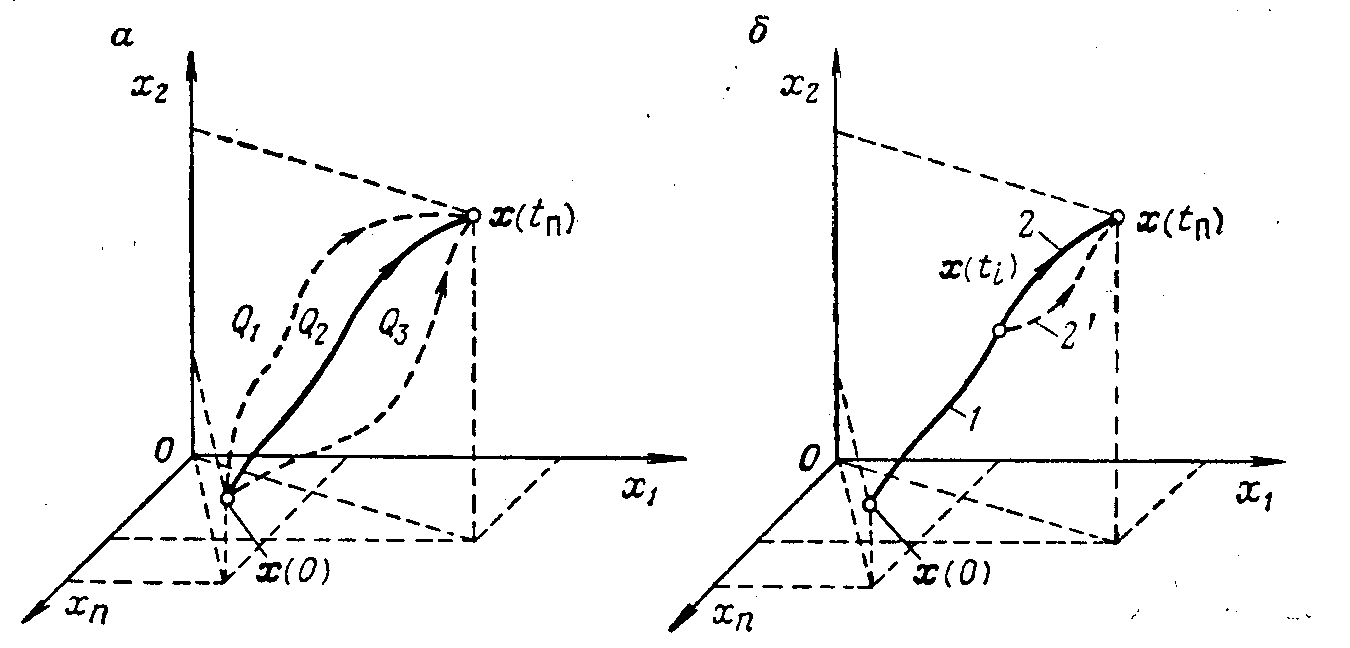
Рис. 6.2. Фазовые траектории в задаче оптимального управления

1—2 (см. рис. 6.2, б), то независимо от того, по какой траектории система пришла в эту точку, оптимальной для начального состояния х (t_i) будет траектория 2. В справедливости такого утверждения нетрудно убедиться, рассуждая от противного. Действительно, если бы между точками х (t_i) и х (t_n) существовала какая-либо другая оптимальная траектория 2', то и для начального состояния х (0) оптимальной была бы не траектория 1 — 2, а траектория 1—2'. А это противоречит исходному условию, что траектория 1—2 оптимальна.

Заметим, что начальный участок 1 оптимальной траектории сам по себе может и не быть оптимальным, т. е. не обеспечить экстремум величины Q в интервале [0, t_i].

Таблица 6.1

Примеры задач оптимального управления

Таким образом, принцип оптимальности указывает общую стратегию оптимального управления: оно должно быть «дальновидным», т. е. экстремизировать показатель оптимальности на всем интервале управления. Попытки добиваться оптимальности на промежуточных этапах могут оказаться невыгодными для задачи в целом.

Принцип оптимальности является основой одного из эффективных методов решения задач оптимального управления — метода динамического программирования.

В изложенной выше постановке задачи оптимального управления предполагалось, что имеется полная информация о состоянии объекта и о внешних воздействиях. Однако часто внешние воздействия имеют вероятностный характер и не могут быть представлены в виде конкретных функций времени. Соответственно и показатель Q является случайной величиной. Эффективность управления при этом целесообразно оценивать по какой-либо статистической характеристике, например по среднему значению показателя Q, вычисленному для определенной совокупности условий. Если Показатель Q является функцией потерь, то его среднее значение называют средним риском.

Система, получаемая в результате решения задачи по статистическому критерию, называется статистически оптимальной. Она осуществляет управление, которое оптимально только в среднем, для всей совокупности рассматриваемых условий. В каждом отдельном случае управление может и не быть оптимальным.

Для решения задачи оптимизации по критерию среднего риска необходимо знать статистические характеристики внешних воздействий.

В последнее время стали применять автоматические системы, реализующие различные игровые стратегии управления. В таких системах используют минимаксный критерий оптимальности, обеспечивающий получение наилучшего результата в наихудшей ситуации.

Недостаток минимаксного критерия в том, что в более легких условиях он дает худшие результаты, чем, например, критерий среднего риска. Поэтому его целесообразно применять лишь тогда, когда неизвестны статистические характеристики внешних воздействий.

Решение задачи оптимального управления и последующая реализация найденного алгоритма в конкретной системе связаны, как правило, с большими трудностями математического и технического характера. Поэтому при создании оптимальных систем стремятся либо предварительно упростить математическое описание объекта, либо реализовать алгоритм приближенно. Такие системы, синтезированные с упрощениями модели объекта или алгоритма управления, называются близкими к оптимальным или квазиоптимальными.

6.2. Системы, оптимальные по быстродействию

Управление, оптимальное по быстродействию, может быть осуществлено как в разомкнутых, так и в замкнутых системах.

Разомкнутые системы (рис. 6.3, а) применяются в тех случаях, когда возмущающие воздействия на объект либо отсутствуют, либо заранее известны (в виде функций времени). Разомкнутая система содержит программное устройство ПУ, которое после пусковой команды выдает заранее рассчитанную программу изменения управляющего воздействия. Причем в устройство может быть заложено несколько программ, оптимальных для различных начальных, состояний объекта.

В замкнутых системах (рис. 6.3, б) оптимальное по быстродействию управление осуществляется при помощи включенного в контур вычислительного устройства ВУ. В это устройство вводятся текущие значения фазовых координат объекта, благодаря чему обеспечивается управление, оптимальное при различных внешних воздействиях.

Рис. 6.3. Функциональные схемы оптимальных по быстродействию систем

Для построения оптимальной замкнутой системы необходимо определить алгоритм функционирования вычислительного устройства в виде зависимости у(х). Общего метода отыскания этого алгоритма не существует. Ниже будет дан пример решения задачи для частного случая.

Синтез оптимальной разомкнутой системы заключается в расчете оптимальной программы у(t). Наиболее общим методом решения этой задачи является принцип максимума, разработанный группой советских математиков под руководством акад. Л. С. Понтрягина.

Рассмотрим вначале сущность принципа максимума Понтрягина применительно к общей задаче оптимального управления (6.7) — (6.10), а затем используем его для синтеза системы, оптимальной по быстродействию.

Введем дополнительную фазовую координату х₀ (t), характеризующую текущее значение функционала (6.4):

(6.11)

(С целью упрощения изложения здесь и далее принято х₃ (t) = 0 и z (t) = 0).

Для этой координаты справедливо следующее дифференциальное уравнение:

(6.12)

Вводя для функции F обозначение f₀ и присоединяя уравнение (6.12) к системе (6.7), можно записать новую систему уравнений:

(6.13)

(j=0; 1; ...; n)

Теперь задача оптимальною управления сводится к отысканию такого решения системы (6.13), при котором дополнительная координата х₀(t) в конце движения принимает наименьшее значение х₀ (t_n)= Q, а остальные переменные удовлетворяют граничным условиям (6.10).

Дли решения задачи, вводятся вспомогательные функции , которые удовлетворяют системе уравнений

(6.14)

Функции можно рассматривать как компоненты некоторого вектора ψ, который равен (по модулю) градиенту функционала Q в (n+1)-мерном фазовом пространстве и направлен в противоположную сторону. Производные фазовых координат также можно считать компонентами вектора f, который характеризует скорость движения изображающей точки в фазовом пространстве.

Согласно принципу максимума оптимальными являются такие управляющие воздействия y₁(t), y₂(t), ..., y_k(t), при которых в каждый момент времени скалярное произведение векторов ψ и f максимально, т. е.

, (6.15)

причем максимальное значение Н равно нулю.

Управляющие воздействия, максимизирующие функцию H, должны, очевидно, удовлетворять следующей системе уравнений:

. (6.16)

Но в этой системе k уравнений содержится (2n + k + 2) неизвестных: (n+ 1) функций x_j (t), (n+1) функций ψ_j(t) и k функций y_l (t). Поэтому для отыскания функций y_l (t) необходимо еще учесть (n + 1) уравнений объекта (6.13) и (n + 1) вспомогательных уравнений (6.14).

Так как функции f_j не зависят от функций ψ_j, то

(6.17)

Учитывая соотношения (6.17), можно уравнения объекта (6.13) и вспомогательные уравнения (6.14) объединить в удобной канонической форме:

(6.18)

Уравнения вида (6.18) называют системой Гамильтона, а функцию Н — гамильтонианом.

Если целью оптимизации является максимальное быстродействие системы, то, как известно из 6.1, f₀=F=1 функция H принимает вид

(6.19)

Применим принцип максимума к линейному объекту n-го порядка с одним ограниченным по модулю управляющим воздействием y. Для этого представим уравнение объекта в виде системы

(6.20)

Управляющее воздействие согласно условию имеет ограничение

(6.21)

Вспомогательные уравнения (6.14) в данном случае имеют вид

(6.22)

а гамильтониан (13.19)

(6.23)

Очевидно, что гамильтониан (6.23) принимает максимальные значения только при

(6.24)

а это означает, что управляющее воздействие у в любой момент времени должно принимать только предельные значения +у_м или – у_м.

Оценим теперь число необходимых переключений управляющего воздействия у_м.

Если все корни характеристического уравнения объекта действительны, то такими же будут и корни характеристического уравнения, соответствующего вспомогательным уравнениям (6.22), и решения системы (6.22) будут иметь вид

(6.25)

При этом управляющее воздействие (13.24) изменяется по закону

(13.26)

Сумма n экспонент, стоящая под знаком sign, может перейти через нуль не более (n-1) раз. Следовательно, оптимальное управляющее воздействие представляет собой кусочно-постоянную функцию (рис.13.4), принимающую только предельные значения ±y_м и имеющую не более n интервалов постоянства.

Рис. 6.4. Управляющее воздействие в системе, оптимальной по быстродействию.

Этот принцип, получивший наименование «теоремы об n интервалах», впервые был сформулирован одним из основоположников отечественной школы теории управления проф. А. А. Фельдбаумом.

Теорема об n интервалах справедлива только для линейных объектов с одним ограничением и при нулевых начальных условиях. При ненулевых условиях число интервалов может быть меньше n. Если ограничение наложено не только на управляющее воздействие, но и на некоторые фазовые координаты, то число интервалов больше n. Причем на каждом из интервалов на предельном уровне находится лишь одна координата.

При наличии у объекта комплексных корней число интервалов может быть сколь угодно большим.

Проиллюстрируем применение принципа максимума на простейшем примере. Пусть объект управления описывается дифференциальным уравнением

(6.27)

Требуется найти законы управления у (t) и у (х), обеспечивающие максимальное быстродействие системы при переходе ее из произвольного начального состояния в равновесное состояние (х = 0, dx/dt = 0). На управляющее воздействие наложено ограничение (6.21), которое в данном случае эквивалентно ограничению второй производной:

, (6.28)

где

Отметим, что уравнение (6.27) соответствует широкому классу механических объектов, в которых происходят процессы перемещения больших масс без трения. Применительно к таким объектам переменная х означает линейное или угловое перемещение, а переменные х’ и х" — соответственно линейные (угловые) скорости и ускорении. Управляющим воздействием y является сила или момент, создаваемые приводом. Коэффициент k₀ в таком случае равен единице, деленной на массу или момент инерции. Электрическая инерционность привода и силы сопротивления при этом не учтены.

Найдем вначале оптимальную программу у (t) разомкнутой системы.

Обозначая х = x₁ и dx/dt = х₂, уравнение объекта можно записать в форме (6.13):

(6.29)

Гамильтониан (6.19) в данном случае равен

(6.30)

Он линейно зависит от переменной у и, следовательно, принимает свои наибольшие значения лишь тогда, когда у (t) = +у_м или у (t) = — у_м. Очевидно, что при ψ₂ (t) > 0 управляющее воздействие должно быть равно +у_м, а при ψ₂ (t) < 0 — значению —у_м. Такой закон управления можно записать при помощи знака sign:

(6.31)

Вспомогательные функции ψ₀, ψ₁, ψ₂ можно найти по уравнениям (6.14), (6.18) или (6.22):

(6.32)

Решения этих уравнений будут:

(6.33)

Отсюда окончательно закон оптимального управления

(6.34)

Так как функция меняет знак не более одного раза, то управляющее воздействие (6.34) представляет собой кусочно-постоянную функцию, имеющую не более двух интервалов постоянства и принимающую только предельные значения +у_м и —у_м.

Момент переключения управляющего воздействия зависит от начальных условий x₁₀ и x₂₀. В наиболее распространенном частном случае, когда х₂₀ = 0, оба интервала равны друг другу (рис. 6.5, б) и в сумме составляют

(6.35)

В более общих случаях определение моментов переключения представляет собой довольно громоздкую вычислительную задачу.

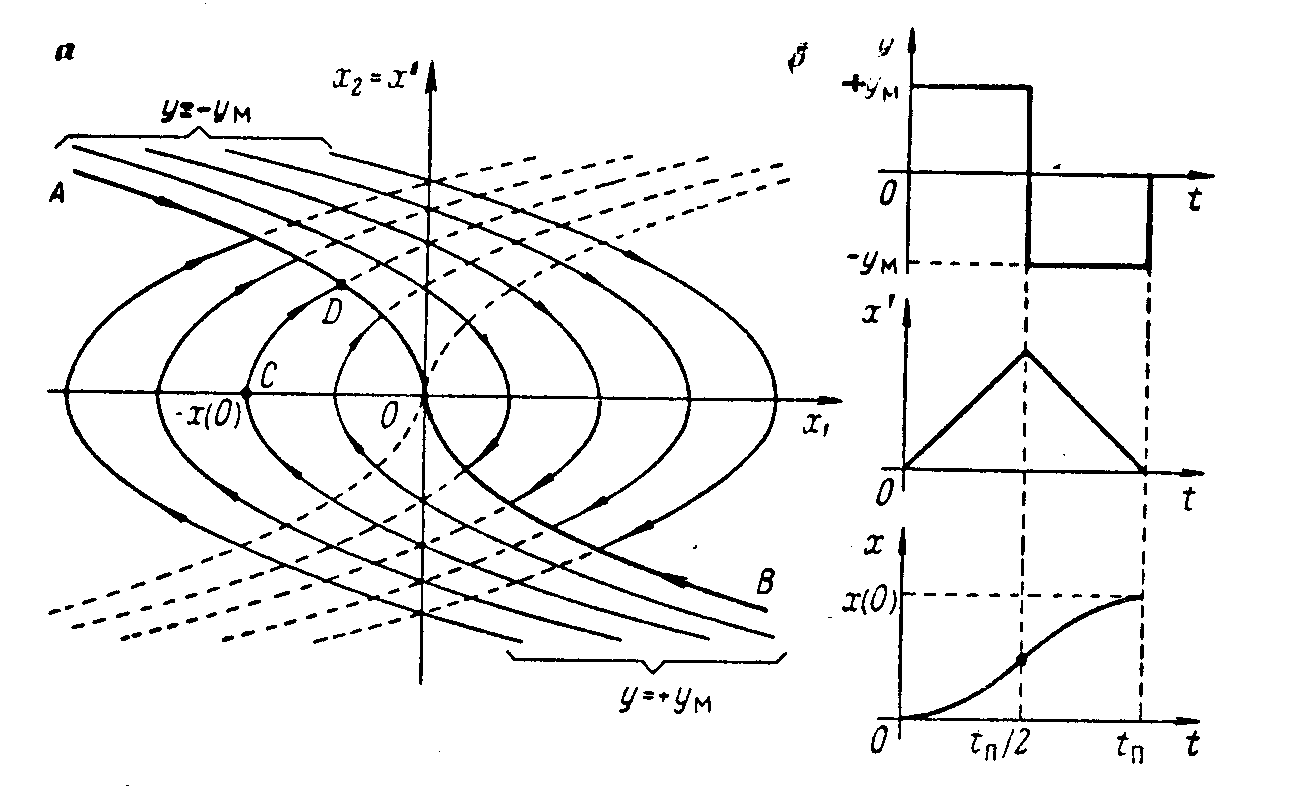
Рис. 6.5. Фазовый портрет (в) и переходные процессы (б) оптимальной системы второго порядка

Полученный закон управления вытекает также из следующих физических соображений. Наибыстрейшее перемещение объекта на величину x₁₀ = х (0) произойдет, если вначале осуществлять разгон с максимально допустимым ускорением +х"_м, а затем после достижения середины пути начать торможение с максимально допустимым замедлением —х"_м (отрицательным ускорением). При этом (см. рис. 13.5, б) скорость перемещения х' на каждом интервале изменяется по линейному закону, а кривая х (t) состоит из ветвей двух парабол.

Синтез управляющего устройства, реализующего максимальное быстродействие в замкнутой системе, осуществим с помощью фазовой плоскости.

Исключая из уравнений (6.29) величину dt, получаем дифференциальное уравнение

(6.36)

Интегрируя выражение (6.36), находим уравнения фазовых траекторий:

при у= + у_м

(6.37)

при y= — у_м

(6.38)

На фазовой плоскости (рис. 6.5, а) уравнению (6.37) соответствует семейство парабол с ветвями, расположенными справа от вершины, а уравнению (6.38) — семейство парабол с ветвями, расположенными слева от вершины. Смещение вершин парабол по оси x₁ определяется постоянными интегрирования С, которые зависят от начальных условий x₁₀ и x₂₀.

Так как по условию задачи процесс должен закончиться в начале координат, то на последнем этапе процесса изображающая точка будет двигаться обязательно по одной из двух парабол, проходящих через начало координат. Причем, согласно общему свойству фазовых траекторий движение к началу координат может происходить лишь по одной ветви каждой параболы: при x₂ >0 — по ветви АО, расположенной во втором квадранте, и при х₂ < 0 — по ветви ВО, расположенной в четвертом квадранте.

Эти две ветви, принадлежащие параболам из разных семейств, можно описать одним общим уравнением

(6.39)

Если в начальном состоянии изображающая точка расположена выше линии АОВ, то под воздействием управления у = —y_м система будет двигаться к завершающему участку ВО по траекториям (6.38). Если же точка расположена ниже линии АОВ, то у = +у_м, и движение происходит по траектории (6.37) до их пересечения с ветвью АО.

В обоих случаях при попадании изображающей точки на линию АОВ происходит переключение управляющего воздействия с одного предельного значения на другое. Таким образом, линия АОВ является линией переключения. Переходным процессам, показанным на рис. 6.5,б, соответствует, конкретная фазовая, траектория CDO.

Теперь, зная уравнение линии переключения, можно синтезировать оптимальное управляющее устройство (рис. 6.6). Оно состоит из двухпозиционного исполнительного устройства ИУ и вычислительного устройства ВУ.

Исполнительное устройство имеет ограниченную выходную величину и описывается функцией

(6.40)

Вычислительное устройство реализует так называемую переключающую функцию

(6.41)

которая на линии переключения (6.39) равна нулю. В точках фазовой плоскости, расположенных правее линии переключения, функция y₁ <0, а управляющее воздействие согласно (6.40) равно у = —у_м. В точках, расположенных левее линии переключения, функция y₁ > 0, а у = +у_м.

Рис. 6.6. Алгоритмическая схема оптимальной системы второго порядка

Рис. 6.7. Фазовый портрет (а) и переходные процессы (б) оптимальной системы с ограниченными ускорением и скоростью

Если у рассматриваемого объекта второго порядка ограничить не только ускорение, но и скорость х' = х₂, то на фазовом портрете оптимальной системы (рис. 6.7, а) появится замкнутая область, за пределами которой действует ограничение х' <x'_м. При достаточно большом начальном отклонении х (0) объект после разгона до предельной скорости х'_м будет некоторое время двигаться с этой постоянной скоростью, а затем начнется торможение с предельным замедлением х"_м (рис. 6.7, б). Такому процессу соответствует фазовая траектория EFGO. Оптимальные процессы с ограниченными значениями скорости и ускорения используют при управлении шахтными подъемными установками.

7. Идентификация систем,

Идентификация – построение оптимальной в некотором смысле модели объекта по наблюдениям за входными и выходными переменными.

Выделяют два типа идентификации:

1. структурная (в широком смысле)

2. параметрическая (в узком)

Основные задачи структурной идентификации: выбор информационных переменных выбор плана объекта, выбор структуры, оценка параметров модели.

Параметрическая идентификация – оценка параметров модели, структура которой известна.

Линейный регрессионный анализ – основа параметрической идентификации.

7.1. Идентифицированность.

САУ является идентифицированной, если по вектору переменных состояний можно определить параметры модели.

Критерий идентифицированности: САУ идентифицирована, если ранг матрицы идентифицированности rank , где n-порядок объекта, .

7.2. Линейный регрессионный анализ.

Ошибка: E=Y-Y_M

J=E² 0

Существуют явные и итерационные методы идентификации.

7.2.1. Явный регрессионный метод.

Для того чтобы осуществить адекватность модели исходному объекту необходимо, чтобы количество наблюдений К было не меньше (n+1), где n-порядок объекта.

K ₁, K₂, T – ?

7.2.2. Итерационный регрессивный метод.

8. Адаптивные системы,.

При проектировании систем автоматического управления обычно исходят из известного характера воздействия на систему и предполагают, что этот характер, а также параметры системы вы процессе функционирования не изменяются или остаются неизменными. Однако в реальных системах характеристики внешних воздействий, а также параметры системы могут изменяться по естественным причинам, например механический износ, Таким образом, синтезированная система управления будет неоптимальной для объекта управления в лучшем случае, или перестанет управлять объектом в худшем случае.

Поэтому необходимо построить такую систему, которая реагировала бы на изменение характеристик внешних воздействий и на изменение параметров объекта. Такие системы называются адаптивными.

8.1. Обобщенная схема адаптивной сау

где Р - регулятор,

О – объект управления,

АА - алгоритм адаптации.

8.2. Классификация адаптивных систем

По замкнутости контуров адаптации.

а) Разомкнутые САУ

Адаптация данных САУ осуществляется по возмущающему воздействию z(t) и по задающему воздействию U(t). В данных системах определяются текущие значения задающего ( U(t)) и возмущающего воздействия (z(t)) и в соответствии с текущей информацией осуществляется перенастройка регулятора. Разомкнутые системы, как правило, применяются редко, так как реакция системы (y(t)) не измеряется.

б) Замкнутые САУ

В замкнутых системах фиксируется реакция системы (y(t)) и задающее воздействие (U(t)) и в зависимости от отклонения выходной величины от заданной, что является следствием изменения параметров объекта, настраивается регулятор.

в) Комбинированные САУ

В комбинированных САУ применяется одновременно адаптация по задающим и возмущающим воздействиям, а также по реакцию системы. То есть данный тип САУ объединяет в себе два предыдущих вида САУ.

По задаче адаптации.

а) САУ со стабилизацией критерия качества управления.

Системы со стабилизацией качества управления поддерживают данный критерий в определенных пределах.

Критерием качества называется показатель, характеризирующий качество управления системы.

Например, в цифровых системах управления по методу переменнного коэффициента усиления таким показателем является быстродействие, а критерий качества имеет вид

б) САУ с автоматической оптимизацией качества управления (системы экстремального управления).

Такие адаптивные системы обеспечивают поиск оптимального значения критерия и осуществляет настройку регулятора в зависимости от этого значения. J=f(x,y,A)

По характеру настройки регулятора.

а) Самонастраивающиеся.

Самонастраивающимися адаптивными САУ называются САУ, в которых в зависимости от изменения параметров объекта изменяются параметры регулятора.

Например , исходным регулятором является ПИ-регулятор:

Однако в процессе функционирования объект изменил параметры, например увеличилась компенсируемая постоянная времени, что влечет за собой изменение (увеличение) , при этом структура регулятора не меняется.

б) Самоорганизующиеся.

Самоорганизующимися адаптивными САУ называются САУ, , в которых в зависимости от изменения параметров объекта изменяется структура регулятора.

Например, в результате изменения параметров объекта ПИ-регулятор не обеспечивает заданные показатели качества системы управления и регулятор меняет свою структуру на ПИД-регулятор.

в) Самообучающиеся.

Самобучающимися адаптивными САУ называются САУ, , в которых в зависимости от изменения параметров объекта изменяется алгоритм управления.

Например, в результате изменения параметров объекта непрерывный характер управления р не обеспечивает заданные показатели качества системы управления и в качестве регулятора применяют цифровой регулятор.

8.3. Применение методов идентификации в адаптивных системах

В адаптивных системах широко применяется процедура идентификации.

В зависимости от реализации различают следующие схемы применения:

1) Адаптивные САУ со встроенной идентификацией.

В процессе функционирования САУ периодически осуществляется процедура идентификации параметров объекта. По полученной модели перенастраивается регулятор.

2) Адаптивная система с эталонной моделью ( ЭМ )

Сигнал с регулятора одновременно подается на объект управления и эталонную модель. Идентификация проводится предварительно, до функционирования САУ при построении эталонной модели. Эталонная модель получается на основе идеальных характеристик объекта.

8.4. Самонастраивающиеся адаптивные системы с автоматической оптимизацией критерия качества управления

Задается некоторый критерий качества J и система настраивается так, чтобы выполнялось условие . В зависимости от оптимизации алгоритма адаптации различают:

поисковые и беспоисковые адаптивные системы.

В поисковых системах автоматическое поддержание критерия качества обеспечивается итерационными методами, а в беспоисковых системах поддержание критерия обеспечивается путем аналитического решения критерия качества.

8.4.2. Поисковые адаптивные сау

Пусть дана исходная САУ и пределен критерий оптимальности как функция некоторых параметров , в качестве параметров могут быть рассмотрены как координаты объекта управления, так и задающие и управляющие воздействия.

Известно, что экстремальное значение критерия достигается при условии:

Однако часто аналитически это уравнения решить либо сложно, либо невозможно, поэтому нп практике применяются итерационные (численные) методы, обеспечивающие:

К итерационным методам относятся:

1. Метод Гаусса – Зейделя;

2. Градиентный метод;

3. Наискорейшего спуска

8.4.2.1. Метод Гаусса – Зейделя

В основе метода лежит исследование производной в точке экстремума

Метод Гаусса-Зейделя предполагает поочередное изменение и определение частных экстремумов при фиксировании всех остальных переменных. Такой цикл повторяется до нахождения экстремума по всем переменным с заданной точностью.

Пример

Пусть критерий оптимальности задан следующей формулой:

Необходимо найти минимум J при начальных значениях

Фиксируем переменную и находим частный экстремум по

Фиксируем переменную и находим частный экстремум по

И так далее до тех пор, пока

8.4.2.2. Градиентный метод

Состоит из двух этапов:

1. Делается пробный шаг по каждому из параметров x_i=x⁰_i+x;

2. Дапее осуществляется рабочий шаг в направлении градиента

Далее повторяется первый этап и так далее, пока градиент:

не станет меьше заданной точности.

8.4.2.3. Метод наискорейшего спуска

Градиентный метод является модификацией градиентного метода. .Движение (поиск оптимального решения) продолжается до тех пор, пока J не перестанет уменьшаться.

8.4.3. Беспоисковые адаптивные сау

В беспоисковых адаптивных САУ обеспечение экстремума может быть осуществлено следующими способами:

1. Предварительное аналитическое нахождение экстремума

и решение данного уравнения программно или аппаратно.

2. С использованием настраиваемой модели.

Процессы, протекающие в модели, являются оптимальными. Алгоритм адаптации осуществляет настройку регулятора таким образом, чтобы значение критерия качества было экстремально.

3. Беспоисковые САУ с вычислением производных

где ЛУ - логическое устройство, определяющее воздействие, обеспечивающее экстремум критерия качества;

ИУ – исполнительное устройство;

ОУ – объект управления;

ДУ – дифференцирующее устройство;

БД – блок деления, обеспечивающий деление .

В системе с помощью ДУ осуществляется вычисление производных . На блоке деления получается сигнал . Логическое устройство ЛУ определяет задающее воздействие , обеспечивающее оптимальное управление объектом.

Литература

1. В. А. Бессекерский, Е. П. Попов Теория систем автоматического управления.— СПб : Профессия, 2004 .— 749 с.

2. В. А. Лукас Теория управления техническими системами: Учеб. пособие для вузов.— Екатеринбург : Изд-во УГГУ, 2005 .— 676 с.

3. Р. Дорф,Р. Бишоп Современные системы управления: Учеб. для вузов— Изд-во «Лаборатория Базовых Знаний», М.: 2004- 832 с.

4. В. Я. Ротач Теория автоматического управления : Учеб. для вузов— М. : Изд-во МЭИ, 2004 .— 399 с.

5. Л. С. Понтрягин Принцип максимума в оптимальном управлении. – М.: Едиториал УРСС, 2004-64 с.

6. Нейросетевые системы управления: Учеб. пособие для вузов/ В. А. Терехов, Д. В. Ефимов, И. Ю. Тюкин. – М.: Высш. шк. 2002.- 183 с.:ил.

7. В. В. Путов Адаптивное управление динамическими объектами: беспоисковые системы с эталонными моделями: Учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2003 .— 92 с.