3.8.1. Алгебраический критерий Шур-Кона

Алгебраический критерий Шур-Кона по характеристическому уравнению замкнутой системы позволяет судить о расположении корней на плоскости z.

Пусть дано характеристическое уравнение замкнутой системы:

(3.64)

Данная система будет устойчива, когда определители Шур-Кона:

и т. д.

где - - сопряженные коэффициенты (для действительных коэффициентов .

Пример

Исследовать устойчивость импульсной системы, характеристическое уравнение замкнутой системы имеет вид

Найдем определители Шур-Кона

=

=

=

По критерию Шур-Кона система устойчива, если нечетные определители – отрицательные, а четные – положительны. Данное условие выполняется, следовательно, система устойчива.

Если система второго порядка, то можно применять упрощенный критерий Шур-Кона: Дискретная САУ будет устойчива, если характеристическое уравнение имеет приведенный вид ( ):

(3.65)

и одновременно выполняются три условия:

1. 

2. (3.66)

3. 

Пример

Исследовать устойчивость импульсной системы, характеристическое уравнение замкнутой системы имеет вид

По критерию Шур-Кона

=

=

Система неустойчива, т. к. второй (четный) определитель отрицательный.

По упрощенному критерию Шур-Кона :

1. 

2. (3.67)

3. 

Система неустойчива, т.к. не выполняется пследнее условие.

Как было сказано выше, методы анализа устойчивости импульсных систем являются аналогами соответствующих методов исследования непрерывных систем. Т. е. для анализа устойчивости импульсных систем можно использовать обычные критерии устойчивости непрерывных систем., но при этом приходится учитывать лишь некоторые особенности импульсных систем.

3.8.2. Критерий Гурвица.

Так, для того чтобы применить критерий Гурвица, необходимо предварительно в уравнении

произвести замену переменной z на переменную  путем подстановки

и получить преобразованное характеристическое уравнение

Корням уравнения (68), расположенным в плоскости корней внутри единичного круга, теперь будут соответствовать корни преобразованного уравнения (70), находящиеся в плоскости корней _k слева от мнимой оси (см. рис. 3.36.). Действительно, если , то модуль числителя в выражении (69) должен быть меньше модуля знаменателя, т.е. . А это возможно лишь в том случае, если вектор _k расположен в левой полуплоскости.

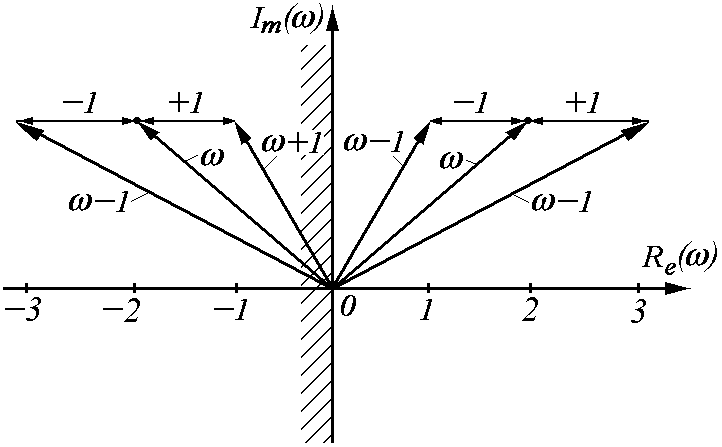
Рис. 3.36.

3.8.3. Критерий Михайлова.

При использовании критерия Михайлова в характеристический полином F(z) подставляют , изменяют  от 0 до /Т и в комплексной плоскости строят годограф вектора F(e^jT). Импульсная система устойчива, если при возрастании  от 0 до /Т характеристический вектор F(e^jT) повернется против часовой стрелки на угол п. Если годограф характеристического вектора проходит через начало координат, то система находится на границе устойчивости. Годографы вектора F(e^jT) для устойчивой и неустойчивой системы второго порядка показаны на рисунке.

Рис. 3.37.