
- •1. Статистический и термодинамический методы исследования. Термодинамическая система. Температура. Идеальный газ. Опытные законы идеального газа.
- •4. Среднее число столкновений и средняя длина свободного пробега молекул. Опытное обоснование молекулярно-кинетической теории.
- •6. Основы термодинамики. Первый закон термодинамики и его применение к изопроцессам.
- •Модели молекул: а- одноатомной, б- двухатомной, в- трехатомной.
- •9. Теплоемкость. Молярная и удельная теплоемкости. Уравнение Майера. Физический смысл универсальной газовой постоянной.
- •10. Изопроцессы. Применение первого начала термодинамики к изопроцессам. Адиабатический процесс. Политропный процесс. Работа газа при адиабатическом процессе.
- •11. Круговой процесс (цикл). Обратимые и необратимые процессы. Кпд кругового процесса.
- •12. Энтропия, изменение энтропии, ее статистическое толкование и связь с термодинамической вероятностью.
- •18. Сжижение газов.
- •19. Свойства жидкостей. Поверхностное натяжение. Смачивание.
- •21. Кристаллические и аморфные твердые тела. Моно- и поликристаллы
- •22. Типы кристаллических твердых тел. Дефекты в кристаллах
- •25. Фазовые переходы I и II рода. Уравнение Клапейрона-Клаузиуса.
- •26. Диаграмма состояния. Тройная точка.
12. Энтропия, изменение энтропии, ее статистическое толкование и связь с термодинамической вероятностью.
Энтропия (S) – термодинамическая функция состояния, которая служит мерой беспорядка (неупорядоченности) системы. Возможность протекания эндотермических процессов обусловлена изменением энтропии, ибо в изолированных системах энтропия самопроизвольно протекающего процесса увеличивается ΔS > 0 (второй закон термодинамики).
Понятие
энтропии было впервые введено
в 1865 году Рудольфом
Клаузиусом.
Он определил изменение
энтропии термодинамической
системы приобратимом
процессе как
отношение общего количества
тепла ![]() к
величине абсолютной
температуры
к
величине абсолютной
температуры ![]() (то
есть тепло, переданное системе, при
постоянной температуре):
(то
есть тепло, переданное системе, при
постоянной температуре):
![]() .
.
В 1877 году Людвиг Больцман установил связь энтропии с вероятностью данного состояния. Позднее эту связь представил в виде формулы Макс Планк:
![]()
где
константа ![]() 1,38·10−23 Дж/К
названа Планком постоянной
Больцмана,
а
1,38·10−23 Дж/К
названа Планком постоянной
Больцмана,
а ![]() — статистический
вес состояния,
является числом возможных микросостояний
(способов), с помощью которых можно
составить данное макроскопическое
состояние. Этот постулат, названный Альбертом
Эйнштейном принципом
Больцмана, положил начало статистической
механике,
которая описывает термодинамические
системы, используя статистическое
поведение составляющих их компонентов
— статистический
вес состояния,
является числом возможных микросостояний
(способов), с помощью которых можно
составить данное макроскопическое
состояние. Этот постулат, названный Альбертом
Эйнштейном принципом
Больцмана, положил начало статистической
механике,
которая описывает термодинамические
системы, используя статистическое
поведение составляющих их компонентов
18. Сжижение газов.
Сжижение газов – перевод вещества из газообразного состояния в жидкое. Сжижение газов достигается охлаждением их ниже критической температуры (Тк) и последующей конденсацией в результате отвода теплоты парообразования. Охлаждение газа ниже ТК необходимо для достижения области температур, при которых газ может сконденсироваться в жидкость
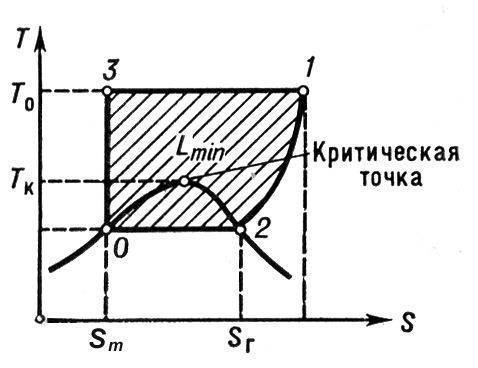
Идеальный цикл сжижения газов.
Изобара 1—2 соответствует охлаждению газа до начала конденсации, изотерма 2—0 — конденсации газа. Площадь ниже 1—2—0 эквивалентна количеству теплоты, которое необходимо отвести от газа при его сжижении, а площадь внутри контура 1—2—0—3 характеризует термодинамически минимальную работу Lmin, необходимую для С. г.:
Lmin= T0(SГ — SЖ) — (JГ - JЖ),
где T0 — температура окружающей среды; SГ, SЖ — энтропии газа и жидкости; JГ, JЖ —теплосодержания (энтальпии) газа и жидкости.
Значения Lmin и действительно затрачиваемой работы LД для сжижения ряда газов даны в таблице.
13----- Второе начало термодинамики. Тепловые двигатели и холодиль ные машины. Теорема Карно. Цикл Карно и его к. п. д. для идеального газа.
Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая, что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю
Из формулировки второго начала термодинамики по Кельвину следует, что вечный двигатель второго рода — периодически действующий двигатель, совершающий работу за счет охлаждения одного источника теплоты, — невозможен. Для иллюстрации этого положения рассмотрим работу теплового двигателя
Цикл Карно́ — идеальный термодинамический цикл. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно. Состоит из 2 адиабатических и 2 изотермических процессов
14---- Силы и потенциальная энергия межмолекулярного взаимодействия
При рассмотрении реальных газов — газов, свойства которых зависят от взаимодействия молекул, надо учитывать силы межмолекулярного взаимодействия. Они проявляются на расстояниях 10–9 м и быстро убывают при увеличении расстояния между молекулами. Такие силы называются короткодействующими.
На рис. 88, а приведена качественная зависимость сил межмолекулярного взаимодействия от расстояния r между молекулами, где Fо и Fп — соответственно силы отталкивания и притяжения, a F — их результирующая. Силы отталкивания считаются положительными, а силы взаимного притяжения — отрицательными.

15---- Уравнение Ван-дер-Ваальса
Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm, а Vm — b, где b — объем, занимаемый самими молекулами.
Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу.
уравнение Ван-дер-Ваальса для моля газа (уравнение состояния реальных газов):
![]()
16--- Изотермы Ван-дер-Ваальса и их анализ
изотермы Ван-дер-Ваальса — кривые зависимости р от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса (61.2) для моля газа.
изотерма называется критической, соответствующая ей температура Tк — критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем Vк, и давление рк называются также критическими. Состояние с критическими параметрами (pк, Vк, Tк) называется критическим состоянием. При низких температурах (Т < Tк ) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.
