3. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и специальной правой частью

Линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами (ЛНДУ) называется уравнение вида

где и некоторые действительные числа.

Уравнение левая часть которого совпадает с левой частью уравнения (..), называется соответствующим однородным уравнением.

Теорема (о структуре общего решения ЛНДУ второго порядка). Общее решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами есть сумма частного решения этого неоднородного уравнения и общего решения соответствующего ему однородного уравнения

Как находить рассматривалось в предыдущем пункте. Нахождение существенно зависит от вида правой части уравнения (..). Будем рассматривать ЛНДУ, у которого правая часть имеет вид:

1. или 2.

где произвольные числа; и многочлены степени и соответственно.

Для этих двух случаев может быть найдено по методу неопределенных коэффициентов, суть которого состоит в следующем. По виду правой части ЛНДУ записывают ожидаемую форму частного решения в форме, соответствующей правой части уравнения с неопределенными коэффициентами. Затем подставляют эту форму частного решения в ЛНДУ и из полученного тождества находят значения коэффициентов.

1. Пусть правая часть ЛНДУ представляет собой произведение показательной функции на многочлен: степень многочлена, постоянная величина. Если то

Тогда частное решение этого уравнения имеет вид:

где кратность, с которой входит в число корней характеристического уравнения; многочлен степени с неопределенными коэффициентами. Очевидно, что может принимать одно из трех значений:

если не является корнем характеристического уравнения;

если однократный корень характеристического уравнения;

если двукратный корень характеристического уравнения.

Отметим, что если то в частном решении не будет сомножителя

Пример… Найти общее решение уравнения

Решение. По теореме о структуре общего решения ЛНДУ второго порядка Значит, решение задачи состоит из двух действий – поиска и

Найдем : характеристическое уравнение Найдем корни квадратного уравнения Следовательно, общее решение однородного уравнения есть функция

Найдем : правая часть Следовательно,

Отсюда, ожидаемая форма частного решения ЛНДУ имеет вид:

где неопределенные коэффициенты.

Найдем первую и вторую производные и подставим их в уравнение:

или

Приравняв коэффициенты при одинаковых степенях в левой и правой частях последнего равенства, получим систему уравнений:

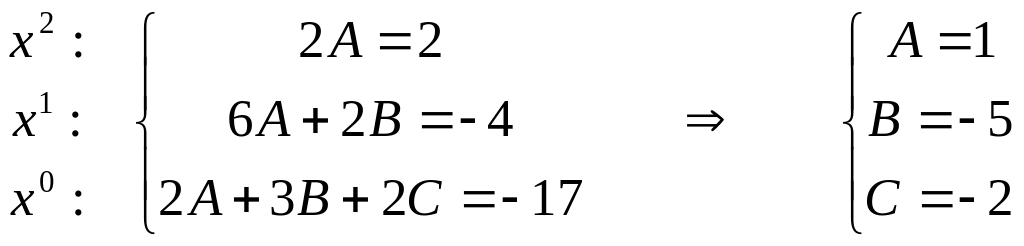
Подставим найденные значения в формулу частного решения . Тогда общее решение ЛНДУ равно

Пример… Найти общее решение уравнения

Решение. По теореме о структуре общего решения ЛНДУ второго порядка Значит, решение задачи состоит из двух действий – поиска и

Найдем характеристическое уравнение Найдем корни квадратного уравнения Следовательно, общее решение однородного уравнения есть функция

Найдем правая часть Следовательно,

Отсюда, ожидаемая форма частного решения ЛНДУ имеет вид:

где неопределенные коэффициенты.

Найдем первую и вторую производные и подставим их в уравнение:

Разделим обе части уравнения на раскроем скобки и приведем подобные:

Приравняв коэффициенты при одинаковых степенях в левой и правой частях последнего равенства, получим систему уравнений:

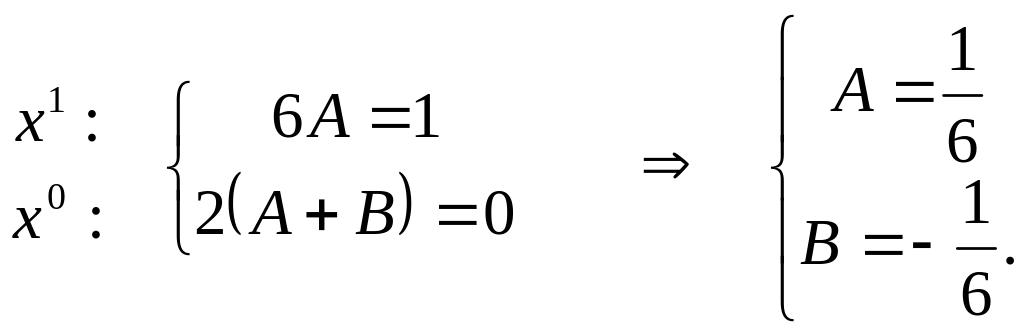
Подставим найденные значения в формулу частного решения . Тогда общее решение ЛНДУ равно

2. Пусть правая часть ЛНДУ представляет собой

где числа

Тогда частное решение этого уравнения имеет вид:

где кратность, с которой чисто мнимое комплексное число входит в число корней характеристического уравнения.

Пример… Найти общее решение уравнения

Решение. По теореме о структуре общего решения ЛНДУ второго порядка Значит, решение задачи состоит из двух действий – поиска и

Найдем : характеристическое уравнение Найдем корни квадратного уравнения Следовательно, общее решение однородного уравнения есть функция

Найдем : правая часть Следовательно, и так как характеристическое уравнение не имеет комплексного корня

Отсюда, ожидаемая форма частного решения ЛНДУ имеет вид:

где неопределенные коэффициенты.

Найдем первую и вторую производные и подставим их в уравнение:

Раскроем скобки и перегруппируем, собрав члены, содержащие и

Приравняв коэффициенты при и в левой и правой частях последнего равенства, получим систему уравнений:

Подставим найденные значения в формулу частного решения . Тогда общее решение ЛНДУ равно