13. Изотермический процесс

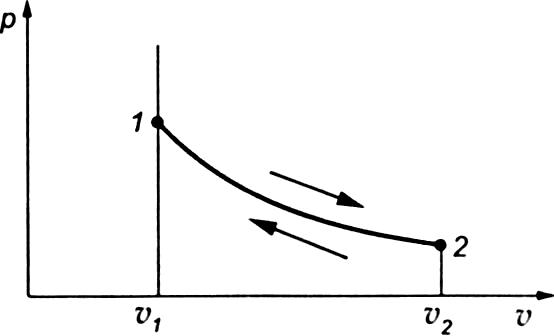Изотермическим процессом называется процесс, протекающий при постоянной температуре: Т= const.

Поскольку в изотермическом процессе Т = const, то уравнение состояния газа pv = RT= const.

В изотермическом процессе в соответствии с законом Бойля—Мариотта справедливо следующее соотношение:

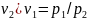(1.11)

или

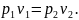
Соотношение (1.11) показывает, что в изотермическом процессе объемы при различных состояниях газа обратно пропорциональны давлениям, соответствующим этим состояниям.

При вычислении внутренней энергии, используя общую формулу (1.6), получим

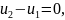
Следовательно, в изотермическом процессе изменение внутренней остается постоянной.

Удельная работа изменения объема в изотермическом процессе определяется уравнением

или

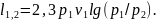(1.12)

На основании первого закона термодинамики

а так как u₂ - u₁ = 0, то

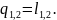
Таким образом, в изотермическом процессе расширения вся подведенная теплота расходуется на внешнюю работу, а при изотермическом процессе сжатия внешняя работа полностью превращается в теплоту.

14. Адиабатный процесс

Адиабатным процессом называют процесс, протекающий без подвода и отвода теплоты:

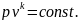(1.13)

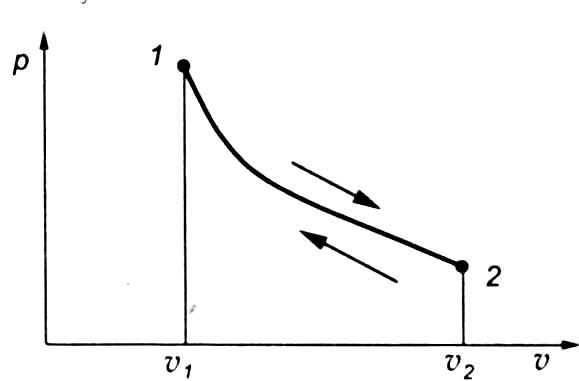где k — показатель адиабаты — величина, равная отношению удельной изобарной теплоемкости к удельной изохорной теплоемкости:

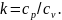
Для идеальных газов k есть величина постоянная, зависящая от природы газа, т. е. от числа атомов в молекуле газа.

Протекание адиабатного процесса без теплообмена с окружающей средой может осуществляться в цилиндре, который имеет идеально теплоизолированные стенки. Однако в природе не существует такой изоляции. Поэтому адиабатный процесс есть идеальный процесс и на практике осуществить его невозможно. Реально можно получить процесс с некоторым приближением к идеальному адиабатному процессу. Например, если процессы протекают очень быстро, т. е. в такое короткое время, что газ не успевает принять или передать теплоту стенкам цилиндра.

Кривая адиабатного процесса называется адиабатой. Она представляет собой неравнобокую гиперболу.

Зависимость между давлением и объемом для двух точек адиабатного процесса имеет вид

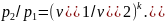(1.14)

Для начального и конечного состояний газа в адиабатном процессе

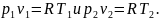
Разделив почленно второе уравнение на первое, получим

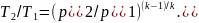(1.16)

Изменение внутренней энергии определяется формулой

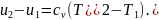
На основании первого закона термодинамики

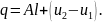
Так как процесс адиабатный, то

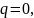
следовательно,

откуда

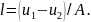
Учитывая, что А — величина постоянная, можно сделать вывод о том, что удельная работа в адиабатном процессе получается только за счет изменения внутренней энергии рабочего тела.

15. Политропный процесс

Политропным процессом называют процесс, в котором могут изме­няться одновременно все параметры газа (р, v, Т), и между газом и окружающей средой осуществляется теплообмен.

Процессы в тепловых машинах, как правило, являются политропными.

Уравнение политропного процесса:

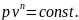(1.17)

где n — показатель политропы.

Если выразить теплоемкость газа в политропном процессе через c_n, то показатель n будет иметь вид

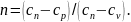
Учитывая, что с_р/с_v = k, получим

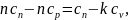
откуда

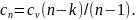
Количество теплоты определяется из уравнения первого закона термодинамики

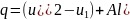
или из уравнения (3):

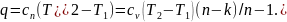(1.18)

Уравнение политропного процесса является общим для всех основных рассматриваемых процессов. Так уравнения изохорного, изобарного, изотермического и адиабатного процессов можно получить из уравнения политропного процесса, если показателю политропы n давать соответствующие значения. Например, если n = ±∞, то уравнение (1.17) примет вид v = const, что соответствует изохорному процессу, если п = 0, то vⁿ = v⁰ = 1, и уравнение (1.17) примет вид р = const, что соответствует изобарному процессу, если п = 1, то уравнение политропного процесса преобразуется в уравнение адиабатного процесса pv^k = const. Таким образом:

• для изохорного процесса n = ±∞,

• для изобарного процесса п = 0,

• для изотермического процесса п = 1,

• для адиабатного процесса п = k.