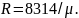6. Законы идеальных газов
В 1662 г. Р. Бойлем, а в 1676 г. независимо от него Э. Мариоттом было доказано, что при постоянной температуре произведение давления газа на его объем постоянно, т. е. в изотермическом процессе расширения или сжатия газа
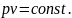
Иначе говоря, при постоянной температуре удельные объемы газа обратно пропорциональны его давлениям:
и
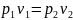(при Т
= const),
где v1 и v2 — удельные объемы в начальном и конечном состояниях газа;
р1 и р2 — соответствующие им давления.
В 1802 г. французский ученый Гей-Люссак открыл закон, согласно которому объем данной массы газа при постоянном давлении меняется линейно с температурой, т. е. для начального и конечного состояний газа
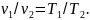
За 15 лет до того, как Гей-Люссак открыл свой закон, французский физик Шарль доказал, что при постоянном удельном объеме изменение давления газа прямо пропорционально его абсолютным температурам:
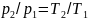(при
v
= const),
или
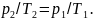
7. Уравнение состояния идеальных газов
Уравнение состояния идеального газа устанавливает связь между всеми тремя основными его параметрами.
Допустим, что идеальный газ, заключенный в цилиндре с поршнем имеет параметры p1, v1 и T1. Если уменьшить давление газа в цилиндре и подвести к нему некоторое количество теплоты, то газ перейдет в новое состояние, где будут иметь место параметры р2, v 2 и Т2
Чтобы установить связь между начальным и конечным состояниями газа, осуществим переход из первого состояния в последнее двумя промежуточными операциями. Сначала уменьшим давление газа от р1 до р2, поддерживая температуру T1 постоянной путем подвода теплоты к газу. Тогда газ окажется в промежуточном состоянии (рис. 2, в) и будет иметь параметры р2, v3 и T1. Затем будем подогревать газ так, чтобы он продолжал расширяться, сохраняя свое давление неизменным, его температура при этом повысится до Т2
Сопоставим эти три состояния газа. Так как в первом состоянии и третьем температуры одинаковы, то между удельными объемами и давлением газа в этих состояниях должна по закону Бойля—Мариотта существовать следующая связь:
,
тогда
.
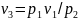Так как в третьем и втором состояниях давления одинаковы, то по закону Гей-Люссака
откуда
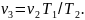
Тогда
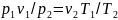
или
.
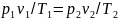Таким образом, отношения произведений давления на удельный объем к абсолютной температуре в любом состоянии газа равны между собой:
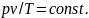
Эту постоянную величину называют удельной газовой постоянной. Обозначив ее буквой R, получим
или
.
Уравнение (называется уравнением идеального газа, или уравнением Клайперона.
Для использования уравнения Клайперона необходимо определить численное значение газовой постоянной для данного газа по справочным материалам. Газовая постоянная становится универсальной, т. е. одинаковой для всех газов, если количество газа выразить в киломолях. Умножив левую и правую часть уравнения (1.1) на мыссу 1 кмоля, получим:
,
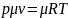где μ — молекулярная масса газа.
На основании закона А. Авогадро, который устанавливает, что при одинаковых температурах и одинаковых давлениях равные объемы различных идеальных газов содержат одинаковое число молекул, было установлено значение универсальной газовой постоянной:
.
Для 1 кмоля газа уравнение состояния можно представить как
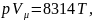(1.2)
где Vμ — объем 1 кмоль газа.
Уравнение (1.2) носит название уравнения Клайперона— Менделеева. Зная значение относительной молекулярной массы μ, можно определить газовую постоянную любого газа:
