2.2. Методы и модели, применяемые в рамках проектирования строительного производства

В настоящее время практически во все отрасли жизнедеятельности человека внедряются автоматизированные системы планирования, организации, оценки, принятия решений для управления сложными системами и процессами, что связано с развитием информационных технологий, совершенствованием возможностей компьютерной техники. Проектирование строительных систем и процессов, в том числе автоматизированное, в обязательном порядке предполагает применение средств математического моделирования, по этой причине ниже приводится классификация и краткая характеристика методов математического моделирования, применяемых для решения задач планирования, организации и управления строительным производством.

Под моделью строительного производства понимается математическое описание взаимосвязей производственных процессов, отображающее с необходимым или возможным приближением к действительности характеристики и параметры технологических, организационных и экономических процессов в строительстве [2].

Объектом моделирования при решении задач управления строительным производством могут быть процессы производства и управления, организационные и информационные структуры, строительные объекты и их комплексы и т.д. Независимо от моделируемого объекта модели строительного производства должны отвечать следующим основным требованиям:

• адекватно отражать существенные черты объекта моделирования;

• отражать динамику строительного производства;

• быть устойчивыми по отношению к несущественным изменениям объекта моделирования;

• обладать простотой и удобством анализа системы.

Задачи организации и управления строительным производством отличаются большой размерностью, высокой степенью сложности взаимосвязи параметров, обладающих чертами – нелинейностью, динамичностью, вероятностным характером, поэтому разработать универсальную модель и единый метод ее реализации достаточно сложно.

Все модели, принимаемые при решении задач организации и управления строительным производством, условно, можно разделить на следующие группы:

1. Математические модели (математического программирования, аналитические и др.).

2. Линейные графические модели (линейные календарные графики, циклограммы).

3. Сетевые модели.

4. Статистические модели.

5. Имитационные логико-арифметические модели.

6. Экспертные системы (модели).

7. Блочно-иерархические модели.

8. Балансовые модели.

9. Логико-смысловые модели.

Математические методы и модели.

Экономической сущностью модели математического программирования обычно является отыскание такого плана, при реализации которого достигается минимум затрат на выполнение определенного объема работ или максимальный эффект при ограниченных ресурсах [ 2 ].

По виду математических выражений различают модели линейного и нелинейного программирования. По степени динамичности модели подразделяются на статические и динамические. Если модель включает целевую функцию, которая обладает свойствами непрерывности, и на переменные не накладываются ограничения целочисленности, то такие модели относятся к классу моделей непрерывного программирования. К классу моделей дискретного программирования относятся такие модели, в которых целевая функция имеет разрывы или на переменные наложено ограничение целочисленности. При детерминированном задании значений целевой функции и ограничений модели относятся к классу детерминированных. Если целевая функция или ограничения заданы случайными величинами, характеризуемыми законами распределения, такие модели относятся к классу моделей статистического программирования.

Наиболее широко в управлении строительным производством применяются модели линейного, нелинейного и динамического программирования.

В общем виде задача линейного программирования формулируется следующим образом:

Определить неотрицательные значения переменных x_i для i от 1 до n , удовлетворяющих системе линейных уравнений

для j от 1 до m минимизирующей линейную функцию

Общая задача нелинейного программирования записывается следующим образом:

Максимизировать (минимизировать) f(x₁, x₂,…,x_n) при условиях g_i(x₁, x₂,…,x_n)  b_i, (i = 1, 2, …, m), (i = 1, 2, …,m; x_i  0).

Основное функциональное уравнение модели динамического программирования имеет следующий вид:

,

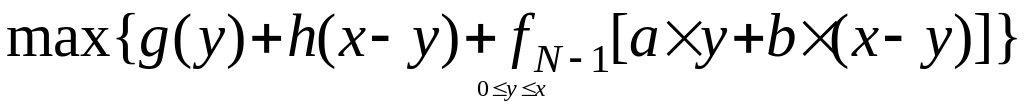где R_N(x, y) – общая отдача от принятой стратегии управления, зависящая от первоначальных затрат у_i и числа этапов управления N;

g(y) + h(x-y) – отдача от первого этапа использования затрат (первоначальные затраты делятся на у и (х-у) и рассматривается отдача от у – g(y) и от (х-у) – h(x-y);

f_N-1 [ay + b(x-y)] – отдача от последующих N-1 этапов управления.

Необходимо отметить, что методы математического программирования применяются, как правило, для решения ресурсных задач – планирования или оптимизации распределения ресурсов строительного производства (складируемых и нескладируемых) во времени и в пространстве с наложением на них определенных ограничений. Модели математического программирования являются эффективным средством решения таких задач строительства, как транспортная задача, оптимальное распределение капиталовложений, распределение трудовых ресурсов, распределения материально-технических ресурсов.