Министерство образования и науки РФ

Федеральное государственное образовательное учреждение

среднего профессионального образования

Кемеровский техникум строительства и эксплуатации

зданий и инженерных сооружений

Основы геодезии

Курс лекций для студентов дневной и заочной форм обучения

Кемерово – 2011

Рассмотрено на заседании Утверждаю:

цикловой комиссии ОПД Зам. директора по УР

Протокол № _________________ «_____» _______2011г.

Председатель ЦК ____________ ____________________

Рекомендовано к изданию учебно-методическим Советом Кемеровского техникума строительства и эксплуатации зданий и инженерных сооружений

«_______»______________2011г. Протокол № ____________________

Рецензенты:

________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Никифорова С.И.

Основы геодезии: Курс лекций для студентов специальности 270802 «Строительство и эксплуатация зданий и инженерных сооружений».

Кемерово: Изд – во Кемеровского техникума строительства и эксплуатации зданий и инженерных сооружений, 2011. – 95с.

Рекомендуется студентам средних профессиональных учебных заведений, обучающихся по специальности 270802 «Строительство и эксплуатация зданий и инженерных сооружений» - Кемерово: Изд-во Кемеровского техникума строительства и эксплуатации зданий и инженерных сооружений.

Никифорова С.И., 2011

Содержание.

Введение __________________________________________________________4

Общие сведения ____________________________________________________5

Масштабы. Условные знаки __________________________________________9

Рельеф местности __________________________________________________14

Ориентирование направлений ________________________________________18

Определение прямоугольных координат _______________________________22

Линейные измерения _______________________________________________26

Технология измерения горизонтальных углов __________________________30

Измерение вертикальных углов ______________________________________39

Способы геометрического нивелирования _____________________________42

Обработка результатов нивелирования ________________________________49

Плановые и высотные сети __________________________________________52

Назначение и виды теодолитных ходов ________________________________55

Камеральная обработка теодолитного хода _____________________________61

Тахеометрическая съёмка ____________________________________________65

Нивелирование поверхности по квадратам ______________________________69

Расчёты при вертикальной планировке участка __________________________71

Трассирование сооружений линейного типа_____________________________73

Введение.

Инженерная геодезия рассматривает комплекс вопросов геодезического обслуживания строительства промышленных и гражданских зданий и сооружений. Решает геодезические задачи, связанные с построением опорной геодезической основы для проведения съёмочных и разбивочных работ; составлением крупномасштабных планов и профилей для проектирования инженерных сооружений; производством разбивочных работ в плане и по высоте при строительстве зданий и сооружений; текущим обслуживанием строительно-монтажных операций; составлением исполнительных чертежей объектов и исследованием их деформаций в процессе строительства и эксплуатации.

Геодезия имеет огромное значение в различных отраслях народного хозяйства. Геодезические работы ведут при планировке, озеленении и благоустройстве. Развитие тяжёлой индустрии, производство электроэнергии, металла, топлива и других отраслей промышленности ставят всё новые задачи перед инженерной геодезией. Комплексная механизация и автоматизация строительно-монтажных операций невозможна без высокой точности геодезических измерений.

В инженерной геодезии всё более широкое применение находят новые методы фотограмметрической съёмки, усовершенствованные автоматические, оптико-механические и электронные приборы, радиогеодезические и спутниковые системы. Исследования деформации земной поверхности и инженерных сооружений в период их строительства и эксплуатации также проводят на основе достижений инженерной геодезии.

Также велика роль геодезии в обороне страны. Карту используют при разработке стратегических планов и проведении военных операций.

Дальнейшее развитие народного хозяйства выдвигает новые задачи перед геодезической наукой, которая должна более активно способствовать развитию всех отраслей промышленности, строительства, транспорта и обороны страны.

Геодезические работы предшествуют и сопутствуют инженерным изысканиям, проектированию, строительству и эксплуатации инженерных сооружений. При проектировании и подготовке выноса проектов зданий и сооружений в натуру составляют разбивочные чертежи. В процессе возведения объектов выполняют контрольные геодезические измерения. После окончания строительства производят исполнительную съёмку и составляют генеральный исполнительный план, используемый при эксплуатации зданий и сооружений. При эксплуатации сооружений ведут систематические геодезические наблюдения за их устойчивостью и прочностью.

Тема : «Общие сведения».

Геодезия – наука об измерениях на земной поверхности, проводимых с целью определения формы и размеров Земли, составления планов и карт, а также решения различных инженерных задач на местности.

Инженерная геодезия - решает задачи, связанные:

• с построением опорной геодезической основы для проведения съёмочных и разбивочных работ;

• составлением крупномасштабных планов и профилей для проектирования инженерных сооружений;

• производством разбивочных работ в плане и по высоте при строительстве зданий и сооружений;

• обслуживанием строительно-монтажных операций;

• составлением исполнительных чертежей объектов;

• наблюдениями за деформациями в процессе строительства.

Физическая поверхность Земли состоит из суши и водной поверхности и имеет сложную форму.

Уровенная поверхность – поверхность воды океанов в состоянии покоя.

Геоид – тело, образованное уровенной поверхностью. Геоид не совпадает ни с одной математической фигурой и представляет собой неправильную форму.

Математическая форма Земли соответствует поверхности эллипсоида, который называется референц – эллипсоид Красовского.

Положение точек на земной поверхности определяется в различных системах координат:

• Система географических координат – за начало отсчёта принимается Гринвичский меридиан и плоскость экватора.

• Система геодезических координат определяет положение точек на поверхности эллипсоида вращения.

• Зональная система прямоугольных координат Гаусса (рис.2).

• Система прямоугольных координат (рис.3).

Рис. 1 Деление на зоны

В такой системе за начало координат для всех зон принимается точка пересечения осевого меридиана данной зоны с экватором. Координатными осями являются ось абсцисс – Х и ось ординат – У.

Абсциссы, отсчитываемые от экватора к северному полюсу, считаются положительными, к южному – отрицательными. Значения ординат от осевого меридиана на восток – положительные, на запад – отрицательные.

Рис.2. Зональная система координат

В геодезии за ось абсцисс принимается направление среднего осевого меридиана зоны, а за ось ординат – направление экватора.

Рис. 3 Система прямоугольных координат

• Полярная система координат. Положение любой точки на плоскости определяется радиус-вектором – r и углом – β, отсчитываемым по ходу часовой стрелки от линии – ОХ (полярной оси) до радиус-вектора (рис.4).

Х А

r

β

О

Рис. 4 Полярная система координат.

Высоты точек могут быть абсолютными и условными. Если высота точки определена от уровенной поверхности, то она считается абсолютной. От любой другой поверхности – условной.

Превышение (h) – разница между высотами точек.

Числовые значения высот точек называются отметками.

В России высоты точек отсчитываются от уровня Балтийского моря.

Рис. 5 Абсолютные и условные отметки.

h_А = Н_А – Н_В

В строительной практике геодезические работы производятся на небольших по размеру участках, которые принимают за плоскость. В результате появляются погрешности в определении расстояний и высот точек. Если изображаемый участок земной поверхности не выходит за пределы круга диаметром 20 км, то его можно принять за плоскость.

На план наносят не сами линии местности, которые часто наклонены к горизонту под некоторым углом, а их горизонтальные проекции.

Проекция измеренной наклонной линии на горизонтальную плоскость, называется горизонтальным проложением.

Тема : «Масштабы топографических

планов и карт. Условные знаки».

Небольшой участок местности, изображённый на бумаге в масштабе 1:1 или меньшем, называется планом. При этом не учитывается кривизна земной поверхности: уровенную поверхность принимают за плоскость.

Для изображения на бумаге больших по размеру участков земной поверхности (круг диаметром более 20 км) или всей Земли составляют сначала планы на отдельные небольшие участки. Затем по математическим законам наносят линии в виде сетки и заполняют её контурами местности и рельефом. Такое изображение больших участков земной поверхности называется картой.

При составлении карт контуры местности проектируют не на горизонтальную плоскость, а на сферическую поверхность. Вследствие чего на карте не сохраняется полное геометрическое подобие контуров местности, нет и постоянного масштаба площадей, так как сферическую поверхность нельзя развернуть на плоскость без складок и разрывов. Это составляет главное отличие плана от карты. На плане масштаб в любой части остаётся постоянным.

План – уменьшенное подобное изображение проекции контуров небольшого участка местности на горизонтальную плоскость.

Карта – уменьшенное подобное изображение проекции контуров местности на горизонтальную плоскость с учётом кривизны Земли.

Все существующие карты по назначению делятся на общегеографические и специальные.

Общегеографические карты в зависимости от масштаба и полноты изображения делятся на обзорные (масштаб мельче 1:1 000 000) и топографические.

Топографические карты являются наиболее подробными. По ним можно выполнять точные измерения при проектировании инженерных сооружений, а также при решении различных инженерных задач. В практике проектирования и строительства зданий и сооружений наиболее широкое применение получили карты масштаба 1:10 000 и крупнее. Их можно использовать как планы.

Специальные карты отличаются от топографических детальным изображением отдельных элементов.

Планы, на которых изображена только ситуация местности, называются ситуационными или контурными.

Планы, на которых кроме предметов местности изображён ещё и рельеф, называются топографическими.

Профиль – уменьшенное изображение вертикального сечения земной поверхности по какому-либо направлению местности.

Разрез – уменьшенное изображение вертикального сечения верхнего слоя земной коры.

В строительном производстве планы, карты и профили используют при разработке проектов строительства.

План, на котором изображён проект размещения всего комплекса сооружений и коммуникаций объекта, называется генеральным планом объекта.

По мере завершения отдельных этапов строительства или отдельных сооружений объекта, результаты строительства наносятся условными обозначениями на генеральный план. Этот документ называется исполнительным генеральным планом. Он служит для оперативного управления строительством объекта.

Масштаб – отношение длины отрезка на плане к соответствующей ему горизонтальной проекции на местности.

Масштаб представляет собой правильную дробь, в которой числитель показывает число единиц на плане, знаменатель – число одноимённых единиц на местности. Масштаб бывает численный (1:500; 1:1000; 1:2000 и т.д.) и графический. Графический делится на линейный и поперечный.

Линейный масштаб представляет собой шкалу с делениями, соответствующими данному численному масштабу.

2 0 2 4 6 8 10

Рис.6 Линейный масштаб

Для более точного построения плана или определения длин линий пользуются поперечным масштабом.

Рис. 7 Поперечный масштаб

Считается, что 0,1 мм – наименьшее расстояние, различаемое человеческим глазом. Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм плана называется точностью масштаба. t = 0,1 мм • М

Для обозначения на планах и картах различных объектов пользуются условными знаками, которые делятся на контурные (масштабные) и внемасштабные, также существуют линейные и поясняющие условные знаки.

Масштабными называют условные знаки, которые служат для изображения объектов местности с соблюдением масштаба карты или плана. Они дают возможность определить не только местоположение предмета, но и его размеры.

Внемасштабные – условные знаки, служащие для изображения объектов, размеры которых не отображаются в данном масштабе карты или плана.

Линейные – условные знаки, служащие для изображения объектов линейного протяжения (автодороги, ж/д дороги, ЛЭП, границы, реки и т.д.).

Рис. 8. Условные знаки:

а – для топографических планов (І – масштабные, ІІ – внемасштабные);

б – для геодезических и строительных чертежей.

Окончание рис.8.

Тема : «Рельеф местности и его изображение на топографических картах».

Рельеф – совокупность неровностей земной поверхности. В зависимости от характера рельефа местность подразделяют на горную, холмистую и равнинную.

Различают пять топографических форм рельефа: гора, котловина, хребет, лощина, седловина.

Гора – куполообразная или коническая возвышенность земной поверхности. В ней выделяют: вершина – самая высокая часть; склоны или скаты, которые расходятся от вершин в разные стороны; подошва – основание возвышенности. Небольшая гора называется холмом или сопкой, искусственный холм – курганом.

Котловина – чашеобразное замкнутое со всех сторон углубление.

Хребет – возвышенность, вытянутая в одном направлении и образованная двумя противоположными скатами. Линия встречи скатов называется осью хребта или водоразделом. Наиболее низкие места водораздела называются перевалами.

Лощина – вытянутое в одном направлении желобообразное углубление с наклоном в одну сторону. Склоны лощины пересекаются по линии, которая называется осью лощины или водосливной линией. Широкая лощина с пологим дном называется долиной, а узкая с крутыми склонами – балкой. В горной местности узкая лощина называется ущельем.

Седловина – понижение между двумя соседними горными вершинами или возвышенностями.

На крупномасштабных планах и картах, служащих для нужд строительства, рельеф изображается горизонталями.

Горизонталь – замкнутая кривая линия, все точки которой имеют одну и ту же высоту, принятую за начальную.

Рис. 9. Формы рельефа местности:

а – основные формы рельефа; б – изображение горизонталями.

Разность высот двух соседних горизонталей называется высотой сечения рельефа.

Заложение – расстояние между двумя смежными горизонталями.

Горизонтали обладают следующими свойствами:

• все точки, лежащие на одной горизонтали, имеют одинаковую высоту;

• все горизонтали должны быть непрерывными;

• горизонтали не могут пересекаться или раздваиваться;

• расстояния между горизонталями в плане характеризуют крутизну ската – чем меньше расстояние (заложение), тем круче скат;

• кратчайшее расстояние между горизонталями соответствует направлению наибольшей крутизны ската;

• водораздельные линии и оси лощин пересекаются горизонталями под прямыми углами;

• горизонтали, изображающие наклонную плоскость, имеют вид параллельных прямых.

Отметки горизонталей подписывают в разрыве горизонтали. Отметки горизонталей всегда кратны высоте сечения рельефа.

Если точка расположена на горизонтали, то её отметка равна отметке горизонтали. Если точка расположена между горизонталями, то через неё проводят прямую линию, перпендикулярную двум соседним горизонталям. Её отметка вычисляется по следующей формуле (рис.10):

Н_А = Н_м.г. + h, где

Н_А – отметка определяемой точки;

Н_м.г. – отметка младшей горизонтали;

d₁ – расстояние от меньшей горизонтали до данной точки (в мм);

d₂ – расстояние между горизонталами (в мм);

h – сечение рельефа. 100,5

100,0

d₂ •

d₁

Рис. 10 Определение отметки точки.

Уклон линии i – отношение превышения h к её заложению d. Уклон i является мерой крутизны ската (рис.11).

i = = tg γ

h = Н_В – Н_А (превышение равно разнице отметок точек)

В

h

γ

А d

Н_А Н_В

Уровенная поверхность

Рис. 11 Определение уклона линии

Следовательно, уклон линии это тангенс угла наклона её к горизонту. Уклоны линий выражают в процентах или промилях. Обычно крутизну ската и уклоны определяют графически с помощью графиков заложений.

Для построения профиля по заданной на карте линии, выбирают масштаб горизонтальный (обычно равен масштабу карты) и вертикальный в 10 раз крупнее. По заданной линии измеряются расстояния между горизонталями и характерными точками перегибов рельефа. Отметки точек откладывают в данном масштабе.

Рис. 12 Построение профиля местности.

Тема : «Ориентирование направлений».

При проведении геодезических работ на строительной площадке возникает необходимость в определении положения линий на местности относительно какого-либо направления, принятого за начальное.

За начальные направления в геодезии принимаются направления:

• Направление истинного меридиана;

• Направление магнитного меридиана;

• Направление среднего осевого меридиана зоны.

Направление истинного меридиана определяется с помощью астрономических наблюдений, магнитного – магнитной стрелки компаса. Направление истинного и магнитного меридианов не совпадает, а образует угол – склонение магнитной стрелки.

Угол δ, отсчитываемый от северного направления истинного меридиана Ν_и до магнитного меридиана Ν_м, называется склонением магнитной стрелки.

Склонение может быть восточным – положительным и западным – отрицательным. При производстве строительно-монтажных работ применяют прямоугольную систему координат, в которой за исходное направление принимается направление среднего осевого меридиана зоны.

Угол γ, отсчитываемый от северного направления истинного меридиана Ν_и до параллели осевому меридиану Ν_о, называется сближением меридианов.

Сближение может быть восточным – положительным и западным – отрицательным.

Для ориентирования линий на местности служат горизонтальные углы: азимуты, румбы и дирекционные углы.

Азимутом А называется угол, отсчитываемый по ходу часовой стрелки от северного направления меридиана до данной линии. Изменяется в пределах от 0^ᵒ до 360^◦.

Ν _и Ν_м

Ν_о

γ

δ

О

Рис. 13 Ориентирование линий на местности

В зависимости от начала отсчёта, азимуты бывают истинными и магнитными.

Истинным азимутом А_и называется угол, отсчитываемый по ходу часовой стрелки от северного направления истинного меридиана до данной линии.

Магнитным азимутом А_м называется угол, отсчитываемый по ходу часовой стрелки от северного направления магнитного меридиана до данной линии.

Дирекционным углом α называется угол, отсчитываемый по ходу часовой стрелки от северного направления осевого меридиана зоны до данной линии.

Все углы изменяются в пределах от 0^◦ до 360^ᵒ.

А_и = α + γ;

А_и = А_м + δ; отсюда

α + γ = А_м + δ;

α = А_м + δ – γ

Ν_и Ν_м

Ν_о

А_и

О А_м α

В

Рис. 14 Азимуты и дирекционные углы

Азимуты и дирекционные углы бывают прямые и обратные.

Ν_о Ν_о

α_АВ

В

α_АВ α_ВА

А

Рис. 15 Прямые и обратные дирекционные углы

α_ВА = α_АВ + 180^ᵒ ; А_ВА = А_АВ + 180^ᵒ – γ ;

Для удобства вычислений пользуются табличными острыми углами, которые называются румбами.

Румбом r называется острый угол между ближайшим северным или южным направлением меридиана и ориентируемой линией.

Румб изменяется в пределах от 0^ᵒ до 90^ᵒ. Для ориентирования линий кроме числового значения румба необходимо указать четверть, в которой он находится.

Зависимость между дирекционными углами и румбами показана на рисунке 16.

Рис. 16 Зависимость между дирекционными углами и румбами

Четверть	Дирекционный угол – α	Румб – r
І четв. СВ	α = r	r = α
ІІ четв. ЮВ	α = 180ᵒ – r	r = 180ᵒ – α
ІІІ четв. ЮЗ	α = 180ᵒ + r	r = α – 180ᵒ
ІV четв. СЗ	α = 360ᵒ – r	r = 360ᵒ – α

Тема : «Определение прямоугольных координат. Прямая и обратная геодезические задачи».

Участки, занятые под строительные площадки, сравнительно небольших размеров, поэтому их можно считать расположенными на плоскости. Положение любой точки на плоскости определяется координатами.

Для определения прямоугольных координат точки, проведём через неё прямые, параллельные осям координат. С помощью измерителя и масштабной линейки измеряем расстояния от точки до координатной сетки. Координаты точки определяются по формулам:

Х_В = Х_n + Х

У_В = У_n + У где

Х_n , У_n – координаты квадрата, внутри которого находится точка В.

Х, У – приращения координат, измеряемые от точки В до сторон квадрата.

Рис. 17. Определение прямоугольных координат.

На строительных площадках обычно принимается условная система координат, начало которой расположено в юго-западной части строительного объекта.

Предположим, на плоскости изображены две взаимно перпендикулярные прямые, которые называются прямоугольными осями координат (рис.18).

Рис. 18.

Точка пересечения осей О называется началом координат. Так как длины отрезков можно откладывать во все стороны (на 360º), то под координатами имеют в виду длины отрезков осей со знаком плюс или минус. Оси координат, пересекаясь в точке О, образуют на плоскости четыре четверти: I, II, III и IV. Тогда знаки по осям абсцисс и ординат будут следующие:

Четверти	I	II	III	IV
Ось абсцисс – Х	+	–	–	+
Ось ординат – У	+	+	–	–

Сущность прямой геодезической задачи состоит в том, что по координатам исходной точки А и полярному углу α направления АВ, требуется определить координаты другой точки В. Так как в практике прямоугольные координаты не измеряют, то для решения задачи измеряют полярный угол α и расстояние d (рис.19).

Рис. 19. Решение прямой и обратной геодезических задач.

Дано: Решение:

Х_А Х_В = Х_А Х

У_А У_В = У_А У

α Х = d , У = d

d

Определить:

Х_В, У_В

Для выноса проекта на местность бывает необходимо по данным прямоугольных координат найти значение дирекционного угла и длину линии между заданными точками. Это и составляет сущность решения обратной геодезической задачи.

Дано: Решение:

Х_А, У_А tg α_А-В = = ; по знакам числителя и знаменателя

Х_В, У_В Определяем название румба линии АВ, а следовательно и

дирекционный угол.

Определить: α_А-В, d_А-В d_А-В = = = = ;

d_А-В = = ;

Рассмотрим примеры решения задач.

Дано: Решение:

Х₁ = 255,35 м Х₂ = Х₁ Х ; У₂ = У₁ У; α = 155^ᵒ 30^′ ; ЮВ: r = 24^ᵒ 30^′

У₁ = 538,80 м Х = d = 98,37 0,90996 = 89,51 м (–)

α = 155^ᵒ 30^′ У = d = 98,37 0,41469 = 40,79 м (+)

d = 98,37 м Х₂ = 255,35 – 89,51 = 165,84 м

Определить: У₂ = 538,80 + 40,79 = 579,59 м

Х₂, У₂

Дано: Решение:

Х₁ = 287,35 м Х_1-2 = Х₂ – Х₁ = 155,85 – 287,35 = – 131,50 м

У₁ = 572,82 м У_1-2 = У₂ – У₁ = 482,32 – 572,82 = – 90,50 м

Х₂ = 155,85 м tg α_1-2 = = = 0,6882 ;

У ₂ = 482, 32 м т.к. Х и У имеют знак (–),

Определить: румб линии будет ЮЗ tg r = 0,6882; r_1-2 = 34^ᵒ 32^′ ,

α_1-2 ; d_1-2 ; соответственно α_1-2 = 180^ᵒ + 34^ᵒ 32^′ = 214^ᵒ 32^′

d_1-2 = = = = ;

d_1-2 = = 159,64 м ; d = = 159,63 м

d_1-2 = = = 159,63 м

за окончательное значение принимаем 159,63 м.

Тема: «Сущность, виды геодезических

измерений. Линейные измерения».

Измерения на земной поверхности проводят с целью установления связи между отдельными точками. Эти измерения позволяют получить данные для решения разнообразных инженерных задач. Для съёмки многоугольника или ломаной линии измеряются прямые линии и углы поворота линий. Если участок местности имеет наклон, измеряются углы наклона прямых линий, чтобы получить их горизонтальные проложения. Чтобы изобразить рельеф местности, определяют высоты точек относительно уровенной поверхности. Таким образом, основными измерениями в геодезии являются линейные и угловые.

При выполнении геодезических работ на местности закрепляют и обозначают точки. В зависимости от срока службы, точки закрепляют временными или постоянными знаками (рис.20).

Рис. 20.

Вертикальная плоскость, проходящая через конечные точки линии, называется створом.

Измерение линий на местности – один из самых распространённых видов геодезических измерений. Без измерения линий не обходится ни одна геодезическая работа. Линии измеряют на горизонтальной, вертикальной и наклонной плоскостях. Их производят рулетками, землемерными лентами, инварными проволоками, а также различными дальномерами. Перед работой мерные ленты и рулетки компарируют, в результате чего мерный прибор может оказаться длиннее или короче контрольного метра.

Процесс сравнения мерного прибора с контрольным метром, называется компарированием.

По результатам компарирования определяют поправку за компарирование, а длину ленты определяют:

l = l_о + Δl_к + Δl_t , где

l_о – номинальная длина ленты;

Δl_к – поправка за компарирование;

Δl_t – поправка за температуру;

Сначала определяют поправку за температуру:

Δl_t = α (t – t_о) l_о , где

α = 12,5 · 10^-6 – коэффициент линейного расширения стали;

t – температура при измерении линий;

t_о – температура при компарировании (принимается равной 20º).

Измерение линий состоит в том, что мерный прибор последовательно откладывают между начальной и конечной точками в створе измеряемой линии. При подготовке створа линии к измерению, её концы фиксируют кольями, штырями, обрезками труб и т.п.; расчищают полосы шириной 1,5 – 2 м от растительности и остатков снесённых строений; забивают колья в местах перегибов местности. Линию на местности обозначают вешками (примерно через 100 м).

Вешение линий производят приёмами «от себя» и «на себя». При вешении «от себя» один мерщик становится с вехой 1 на исходной точке, а второй – на конечной точке устанавливает веху 2 такой высоты, чтобы она была видна с исходной точки. Второй мерщик перемещает веху 3 по створу линии до конечной точки. Между вехами измеряются расстояния. При вешении «на себя» мерщик выставляет вешку в створе двух других вех, имея их перед собой.

Для контроля линию измеряют вторично в обратном направлении. За окончательное значение принимают среднее арифметическое от измерений в прямом и обратном направлениях. Измерения считают выполненными, если расхождения в результатах прямого и обратного направлениях не превышают:

1:3000 от измеряемой длины – при благоприятных условиях измерений (твёрдое покрытие);

1:2000 – при средних условиях измерений (ровная поверхность грунта);

1:1000 – при неблагоприятных условиях измерений (болотистая, заросшая, кочковатая местность, измерения по снегу).

При построении карты и плана местности пользуются горизонтальными проекциями линии местности. Линейные измерения производят по поверхности рельефа местности, имеющего уклоны. Для приведения наклонно измеренных линий к горизонтальным, в результаты измерений вводится поправка за наклон линии к горизонту – ΔD. Чтобы получить проекцию – d измеренной на местности линии – АВ длиной – D, необходимо измерить угол наклона – γ (рис.2). Горизонтальное проложение определяется:

d = D · или d = D – ΔD

где ΔD = 2D ·

Горизонтальные проложения обычно вычисляются по специальным таблицам. Если известны превышения между точками А и В, то поправку ΔD вычисляют:

ΔD =

Рис. 21.

При больших углах наклона местности, измерения линий ведут отдельными не большими отрезками по 5 – 10 м, стараясь уложить концы мерного прибора горизонтально. Суммарная поправка в измеренную линию вычисляется:

Δl = Δl_h + Δl_к + Δl_t

Измерение линий на местности производят непосредственно и косвенно. Непосредственные измерения производят мерными приборами, а косвенные дальномерами различных типов. В настоящее время широкое применение получили лазерные дальномеры.

Тема: «Угловые измерения. Технология измерения горизонтальных углов».

Принцип измерения горизонтального угла состоит в следующем. Предположим на поверхности Земли имеются три точки А, В и С, расположенные на разных высотах над уровнем моря (рис.22). Требуется определить горизонтальную проекцию угла АВС. Спроектировав эти точки на произвольную горизонтальную плоскость, получим их горизонтальные проекции А₁, В₁, С₁. Линии В₁С₁ и В₁А₁ являются горизонтальными проекциями ВС и ВА; угол А₁В₁С₁ = β является горизонтальной проекцией угла АВС. Угол β – линейный угол двугранного угла, составленного вертикальными плоскостями АА₁В₁ и СС₁В₁. Для определения его значения в градусной мере, круг с градусными делениями располагаем над точкой В так, чтобы его центр оказался на отвесной линии ВВ₁. Если вращать вертикальную плоскость, проходящую через точку В, вокруг отвесной линии ВВ₁, последовательно совмещая её сначала с точкой С, а затем с точкой А, то величина угла β будет равна разности дуг а – с, выраженной в градусной мере.

Рис. 22.

На местности измерения горизонтальных и вертикальных углов производится прибором, называемым теодолитом. Теодолиты в зависимости от точности разделяются на высокоточные, точные и технические. К последней группе относятся теодолиты, применяемые в строительное- монтажном производстве (Т – 30, 2Т - 30), средняя квадратическая погрешность измерения углов в таких теодолитах составляет 30ʹʹ. Схема устройства теодолита представлена на рисунке 23. Теодолит имеет стеклянный или металлический лимб, разделённый по окружности на 360º. Над лимбом установлен вращающийся круг –алидада.

К подставкам теодолита прикреплена зрительная труба, вращающаяся в вертикальной плоскости вокруг оси НН₁.

Ось ZZ₁ является вертикальной осью вращения прибора. В горизонтальное положение теодолит приводится с помощью трёх подъёмных винтов (17) и цилиндрического уровня (4). На оси вращения трубы наглухо с ней прикреплён вертикальный круг (9). Он может располагаться справа или слева от зрительной трубы; первое положение называется «круг право» – КП, второе положение «круг лево» – КЛ. В комплект теодолита входят буссоль, штатив и отвес. Теодолит крепится к штативу с помощью станового винта. Вращающиеся части теодолита снабжены закрепительными винтами (1,2,8) для закрепления их в неподвижное состояние и наводящими винтами (3,5,16) для точного ориентирования прибора по заданному направлению (рис.24).

Рис. 23

1 – лимб горизонтального круга

2 – алидада горизонтального круга

3 – зрительная труба

4 – подставка

5 – алидада вертикального круга

6 – лимб вертикального круга

7 – уровень при горизонтальном

8 – подъёмные винты

9 – головка штатива

10 – становой винт

J J₁ – вертикальная ось вращения теодолита

U U₁ – ось цилиндрического уровня горизонтального круга

Н Н₁ – горизонтальная ось вращения трубы

V V₁ – визирная ось зрительной трубы

Чтобы обеспечить ожидаемую точность измерения углов, теодолит должен удовлетворять определённым оптико – механическим и геометрическим условиям. Первые условия обычно гарантирует завод – изготовитель. Геометрические условия чаще всего подвержены изменениям в процессе работы и транспортировки прибора. Поэтому геометрические условия необходимо проверять перед началом полевых работ. При геодезическом обслуживании строительно-монтажных работ малейшее несоблюдение этих условий вызовет брак, особенно при монтаже строительных конструкций. В связи с этим требуется систематически выполнять поверки теодолита. Каждая поверка состоит из двух частей: 1) выявления нарушения или соблюдения данного условия; 2)исправления (юстировки) положения соответствующей части инструмента для устранения нарушения поверяемого условия.

Рис.24

Поверки – это действия, которыми контролируют правильность взаимного расположения осей.

1 – я поверка.

Ось цилиндрического уровня при алидаде горизонтального круга должна быть перпендикулярна вертикальной оси вращения теодолита ( U U_{1 ┴} J J₁).

Порядок подготовки. Перед выполнением поверки проводят предварительное нивелирование теодолита. Для этого устанавливают уровень параллельно плоскости двух подъёмных винтов и вращением этих винтов в разные стороны приводят пузырёк уровня в нульпункт. Далее поворачивают верхнюю часть теодолита на 90º и вращением третьего винта приводят пузырёк уровня на середину.

Порядок поверки. Устанавливают уровень в плоскости двух подъёмных винтов, вращением этих винтов в разные стороны, приводят пузырёк уровня в нульпункт. Ослабляют закрепительный винт алидады и поворачивают верхнюю часть теодолита на 180º. Если пузырёк уровня остался на середине или сместился менее чем на одно деление, то условие выполнено. В противном случае проводят юстировку.

Порядок юстировки. Действуя исправительными винтами, перемещают пузырёк уровня к нульпункту на половину дуги отклонения, другую половину устраняют подъёмными винтами. Эти действия повторяют до тех пор, пока пузырёк уровня будет отклоняться от середины не более чем на одно деление.

Исправительные винты вращают с помощью специальной шпильки. Если пузырек уровня требуется сместить по направлению к исправительным винтам, то следует ослабить верхний винт и подтянуть нижний. Перемещение пузырька начинают с ослабления одного из винтов. Вращают их в одном направлении.

2 – я поверка.

Визирная ось зрительной трубы должна быть перпендикулярна горизонтальной оси вращения трубы (V V_{1 ┴} Н Н₁).

Порядок подготовки. Приводят вертикальную ось теодолита в отвесное положение (нивелирование теодолита). Выполняют также, как и перед первой поверкой.

Порядок поверки.

Закрепляют лимб и поворотом алидады наводят перекрестие сетки нитей на точку, примерно расположенную на одном уровне с теодолитом. Берут отсчёт по горизонтальному кругу – КЛ, результат записывают в журнал (табл.1). Переводят трубу через зенит и наводят зрительную трубу на ту же точку, берут отсчёт по горизонтальному кругу – КП, результаты заносят в журнал.

Погрешность, которую называют коллимационной, вычисляют по формуле:

С =

Если коллимационная погрешность по абсолютной величине не превышает двойной точности отсчётного устройства, условие выполнено.

│С│ 2t

Если │С│ 2t, производят юстировку.

Порядок юстировки. Вычисляют свободный от влияния коллимационной погрешности отсчёт:

N =

и устанавливают его на лимбе (табл.1). Перекрестие сетки нитей при этом сойдёт с наблюдаемой точки. С помощью исправительных винтов, сетку нитей совмещают с изображением точки. После выполнения юстировки, поверку повторяют.

Таблица 1.

Точкавизирования	Отсчёт по горизонтальному кругу		Вычисления
	КЛ	КП
До юстировки
1	30º 29ʹ	210º 21ʹ	С1 = = + 4ʹ 2t = 2ʹ
После юстировки
1	30° 24ʹ	210° 25ʹ	N = 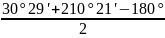= 30°25ʹ С2 = = – 30ʹʹ

3 – я поверка.

Горизонтальная ось вращения зрительной трубы должна быть перпендикулярна оси вращения прибора (НН_{1 ┴} JJ₁).

При подготовке к поверке необходимо вертикальную ось теодолита привести в отвесное положение (нивелирование теодолита).

Порядок поверки. На расстоянии 20 – 30 м от стены здания устанавливают теодолит и наводят перекрестие сетки нитей на точку М в верхней части стены. Опускают зрительную трубу до уровня высоты теодолита и отмечают на стене точку М₁, на которую проецируется перекрестие сетки нитей. Переводят трубу через зенит и повторяют те же действия при другом положении круга, отмечают точку М₂ (рис.25).

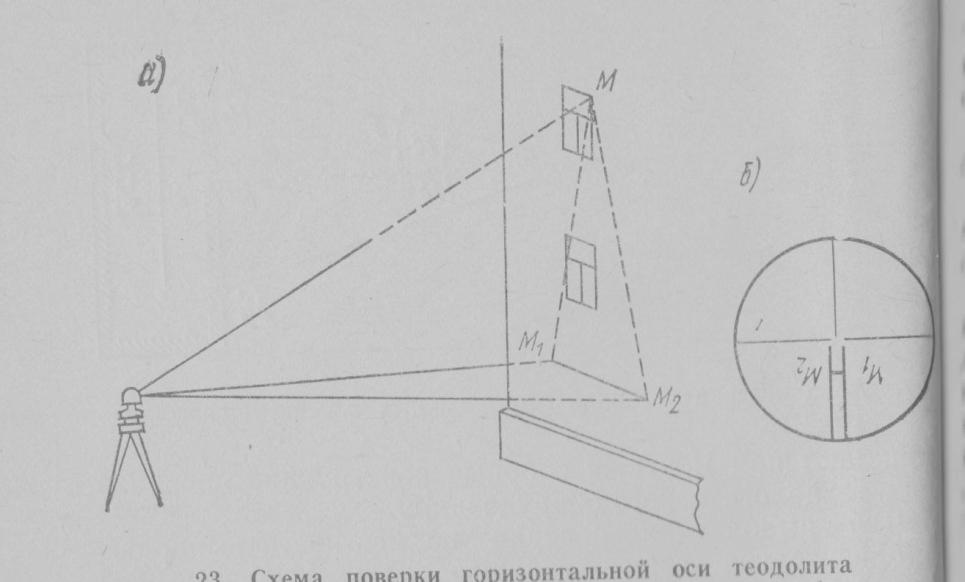
Рис.25

Если в поле зрения трубы отрезок ММ₁ укладывается в биссекторе сетки нитей, то условие считают выполненным.

Юстировку производят только в оптико-механических мастерских, либо на заводе изготовителе.

4 – я поверка.

Сетка нитей зрительной трубы должна быть поставлена правильно.

Порядок поверки. Для выполнения поверки приводят теодолит в рабочее положение (нивелируют). Наводят зрительную трубу на точку (которую можно обозначить на стене здания) так, чтобы изображение её оказалось совмещённым с одним из концов вертикальной сетки нитей. Затем плавно перемещают зрительную трубу вверх или вниз наводящим винтом. Если изображение точки совпадёт с нитью на всём её протяжении, то условие выполнено. В противном случае производят юстировку.

Порядок юстировки. Ослабляют винты, закрепляющие окулярную часть, и поворачивают её вместе с сеткой нитей до совмещения вертикальной нити с наблюдаемой точкой. После этого повторяют поверку 2.

Для измерения горизонтальных углов выверенный теодолит устанавливают в вершине измеряемого угла, производят центрирование и нивелирование инструмента (приводят теодолит в рабочее положение).

Центрирование теодолита заключается в том, чтобы отвес располагался над центром геодезического знака и одновременно столик штатива принял бы горизонтальное положение (на глаз).

Нивелирование теодолита состоит в установке вертикальной оси прибора в отвесное положение (подготовка к первой поверке).

Измерение горизонтальных углов производится полным приёмом, который состоит из двух полуприёмов.

1-й полуприём – (КП). Для измерения горизонтального угла закрепляют лимб горизонтального круга и при откреплённой алидаде наводят зрительную трубу на заднюю точку В по ходу визирования. Закрепив закрепительными винтами алидаду и зрительную трубу, совмещают перекрестие сетки нитей с точкой В наводящими винтами алидады и зрительной трубы. Берут отсчёт по горизонтальному кругу (в_n), результат заносят в журнал измерения горизонтальных углов (табл.2). Открепляют зрительную трубу и вращением алидады наводят её на переднюю точку А. Берут отсчёт по горизонтальному кругу (а_n), результат заносят в журнал измерения горизонтальных углов. Вычисляют значение угла в полуприёме как разницу между отсчётами на заднюю и переднюю точки (рис.7).

Рис.26

β_n = в_n - а_n

2-й полуприём – (КЛ). Переводят трубу через зенит, открепляют алидаду и наводят на заднюю точку В. Берут отсчёт по горизонтальному кругу (в_л). Затем наводят на переднюю точку А и берут отсчёт (а_л). Результаты заносят в журнал измерения горизонтальных углов. вычисляют значение угла во втором полуприёме.

β_л = в_л – а_л

Журнал измерения горизонтальных углов.

Пример оформления. Таблица 2.

Точка стояния	Точка визирования	Отсчёты по горизонтальному кругу	Значение угла из полуприёма	Среднее значение угла
А	2 КП 1	87º 47ʹ 53º 21ʹ	34º 26ʹ	34º 25ʹ 30ʹʹ
	2 КЛ 1	267º 46ʹ 233º 21ʹ	34º 25ʹ

Вычислив значения угла в первом и втором полуприёмах, сравнивают их величины. Расхождения значений углов в полуприёмах по абсолютной величине не должны превышать двойной точности отсчитывания теодолита.

│Δβ│ = │β_л - β_n│ 2t

Если условие соблюдается, то за окончательное значение принимают среднее .

β =

Если условие нарушено, угол измеряют заново.

Тема: « Технология и контроль измерений и вычислений вертикальных углов».

Вертикальный угол – это угол между горизонтальной плоскостью и направлением визирной оси на какую-либо точку (рис.27).

Рис.27

Для измерения вертикальных углов служит вертикальный круг теодолита. При измерении вертикальных углов визирная ось зрительной трубы должна быть параллельна нулевому диаметру лимба. Если это условие нарушено, то при горизонтальном положении визирной оси вместо нуля будет другое значение. Этот отсчёт называют местом нуля и обозначают МО.

Место нуля - это отсчёт по вертикальному кругу при горизонтальном положении визирной оси и положению пузырька уровня при алидаде вертикального круга в нульпункте или горизонтальности отсчётного индекса у теодолитов с компенсатором при вертикальном круге.

Место нуля исправного теодолита будет величина постоянная и не должна превышать двойной точности отсчитывания теодолита. Если МО превышает допустимое значение, то производят его исправление. Для этого сначала вычисляют вертикальный угол γ.

МО 2t

При работе с теодолитом Т – 30 место нуля вычисляют по формуле:

МО =

Угол наклона – γ вычисляют:

γ = МО – КП + 180° или γ = КЛ - МО

При работе с теодолитом 2Т – 30 место нуля вычисляют:

МО =

Угол наклона – γ вычисляют:

γ = МО – КП или γ = КЛ – МО

Исправление МО.

Вращением наводящего винта зрительной трубы устанавливают на вертикальном круге отсчёт, равный вертикальному углу γ. При этом пузырёк уровня на горизонтальном круге должен находиться в нуль-пункте. Затем, действуя вертикальными исправительными винтами при сетке нитей, смещают сетку так, чтобы её горизонтальная нить совпала с изображением точки визирования. После закрепления сетки повторно определяют МО.

Вертикальные углы – углы наклона измеряют при двух положениях круга (круг «лево» – КЛ и круг «право» – КП). Для измерения наводят зрительную трубу на точку, берут отсчёт по вертикальному кругу (КП). Переводят трубу через зенит, наводят на ту же точку и берут отсчёт по вертикальному кругу (КЛ). Подставляют значения в соответствующие формулы и вычисляют углы наклона (пример прилагается). Все значения заносят в журнал измерения вертикальных углов (табл.3).

Углы наклона могут быть положительные и отрицательные.

Положительный угол образуется разностью между направлением на предмет, расположенный выше уровня горизонтальной оси вращения трубы, и направлением, соответствующим горизонтальному положению визирной оси.

Отрицательный угол – угол между горизонтальным положением визирной оси трубы и направлением на точку, расположенную ниже горизонтальной оси вращения трубы.

1

+γ

А -γ

2

Рис.28

Журнал измерения вертикальных углов.

Пример оформления. Таблица 3.

Точка стояния	Точка визирования	Отсчёт по вертикальному кругу	МО место нуля вертикального круга	γ Угол наклона
А	1 КЛ	1° 09ʹ	– 0° 00ʹ 30ʹʹ	1° 09ʹ 30ʹʹ
	1 КП	178° 50ʹ
А	2 КЛ	356° 54ʹ	0° 00ʹ 00ʹʹ	– 3° 06ʹ
	2 КП	183° 06ʹ

Пример вычислений (для теодолита – Т-30).

При измерении на точку 1 (точка расположена выше линии горизонта).

МО₁ = = – 0° 00ʹ 30ʹʹ

γ₁ = – 0° 00ʹ 30ʹʹ – 178° 50ʹ + 180° = + 1° 09ʹ 30ʹʹ

γ₂ = 1° 09ʹ – ( – 0° 00ʹ 30ʹʹ) = + 1° 09ʹ 30ʹʹ

При измерении на точку 2 (точка расположена ниже линии горизонта).

МО₂ = = = 0° 00ʹ 00ʹʹ

γ₂ = 0° 00ʹ – 183° 06ʹ + 180° = – 3° 06ʹ

γ₂ = 356° 54ʹ – 0° 00ʹ – 360° = – 3° 06ʹ

Тема: «Принцип и способы геометрического нивелирования. Устройство нивелира».

Нивелирование проводится для определения высот точек земной поверхности, необходимых для изучения рельефа местности и изображения его на планах и картах. Обычно определяют превышения между отдельными точками и, зная абсолютную отметку одной из них, вычисляют отметки остальных. В геометрическом нивелировании превышения определяются с помощью горизонтального луча визирования и вертикальных реек, по которым берутся отсчёты. Горизонтальное визирование осуществляется геодезическим прибором – нивелиром.

Геометрическое нивелирование осуществляют способами:

• Нивелирование из середины

• Нивелирование вперёд.

Нивелирование из середины. При нивелировании из середины в точках устанавливают рейки, а между ними посередине – нивелир (рис.29).

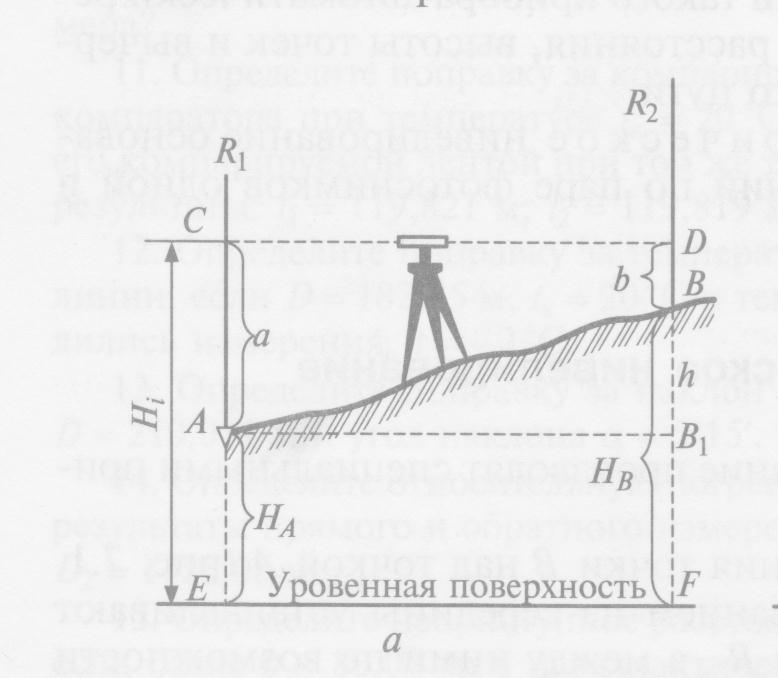
Рис.29

Для определения превышения точки В над точкой А, устанавливают рейки в этих точках R₁ и R₂, а между ними нивелир. Последовательно визируют на рейки средней горизонтальной нитью зрительной трубы, берут отсчёты: а – по задней рейке и b – по передней рейке. Превышение h определится, как отсчёт по задней рейке минус отсчёт по передней рейке.

h = а – b

Превышение может быть положительным если а , и отрицательным при а .

Зная абсолютную отметку Н_А точки А, можно определить отметку точки В

Н_В = Н_А + h,

т.е. отметка передней точки равна отметке задней точки плюс превышение h между ними.

Н_В = Н_А + а - b

Если с одной стоянки нивелира производят нивелирование нескольких точек, то отметки этих точек принято считать через горизонт инструмента.

Горизонтом инструмента называется высота луча визирования над уровенной поверхностью.

Горизонт инструмента – ГИ равен отметке задней точки плюс отсчёт по рейке, установленной в этой точке:

ГИ = Н_А + а,

тогда при определении отметки любой точки, в эту точку ставят рейку и берут отсчёт и производят вычисления:

Н_В = ГИ – b,

т.е. отметка любой точки равна горизонту инструмента минус отсчёт по рейке, установленной в данной точке.

Нивелирование вперёд. Для определения превышения при нивелировании вперёд над точкой с известной отметкой устанавливают нивелир, а в другую точку (отметку которой нужно найти) ставят рейку. Рулеткой измеряют высоту инструмента – i (от верха колышка до визирной оси зрительной трубы), а по рейке берут отсчёт – b (рис.30).

h = i – b

Превышение h равно высоте инструмента минус отсчёт по передней рейке. Следовательно, зная отметку исходной точки А и вычисленное превышение, определяют отметку точки В.

Н_В = Н_А + h

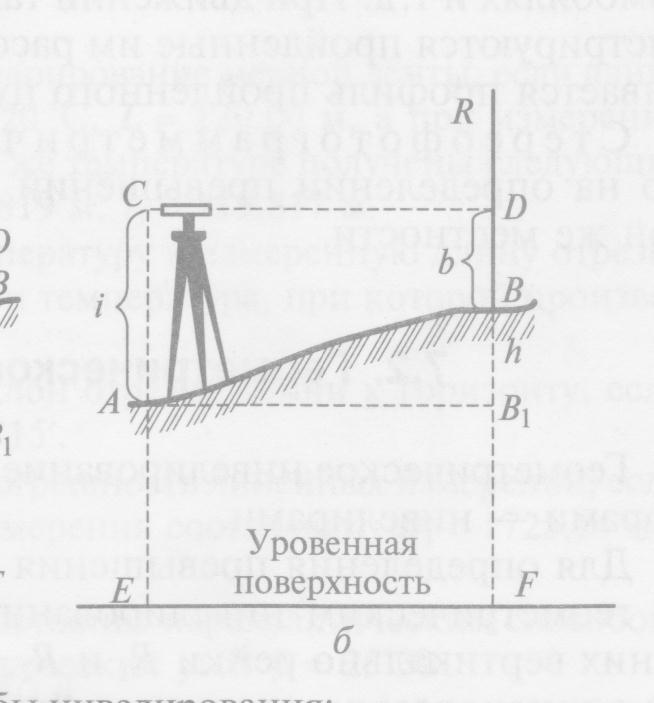
Рис.30

В тех случаях, когда расстояния между начальной и конечной точками превышает допустимое расстояние между нивелиром и рейкой или когда превышения между конечными точками значительно больше длины рейки, выполняют сложное нивелирование (рис.31).

Рис.31

Для этого расстояние между конечными точками разбивают на отрезки и последовательно определяют превышения h₁, h₂, h₃, и т. д.

h₁ = а₁ – b₁ ; h₂ = а₂ – b₂ ; h₃ = а₃ – b₃ ;

Тогда превышение h_АВ между конечными точками А и В, определяется:

h_АВ = h₁ + h₂ + h₃ + … + h_n

Зная отметку начальной точки Н_А, вычисляют отметку конечной точки:

Н_В = Н_А + h_АВ

Нивелиры в зависимости от точности разделяются на высокоточные, точные и технические. Рассмотрим глухой нивелир с цилиндрическим уровнем типа Н – 3, который относится к классу точных. Главным требованием, предъявляемым к таким нивелирам, является параллельность оси цилиндрического уровня и визирной оси трубы. Нивелир Н – 3 состоит из верхней части, несущей зрительную трубу – 6 с цилиндрическим – 7 и круглым – 3 уровнями, наводящим – 11, элевационным – 4 и закрепительным – 9 винтами, и нижней, представляющей собой подставку с

Тремя подъёмными винтами – 1 и прижимной пластиной – 10 (рис.32).

Рис.32

Установка нивелира в рабочее положение производится таким же способом, как и первая поверка теодолита, но исправление уровня производится элевационным винтом.

ZZ₁ – вертикальная ось вращения нивелира;

VV₁ – визирная ось зрительной трубы;

UU₁ – ось цилиндрического уровня;

ОО₁ – ось круглого уровня.

На рисунке 33 изображено взаимное расположение осей нивелира.

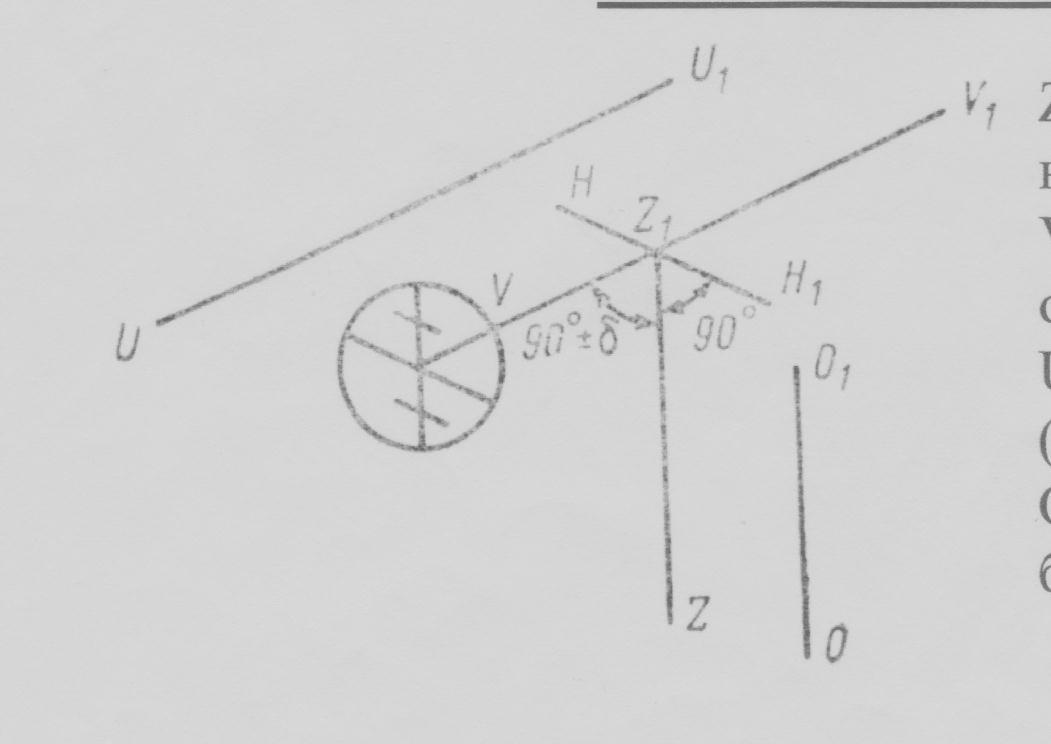
Рис.33

1 – я поверка.

Ось круглого уровня ОО₁ должна быть параллельна оси вращения нивелира ZZ₁ (ОО₁ || ZZ₁).

Вращением подъёмных винтов приводят пузырёк уровня на средину и поворачивают его на 180°. Если условие выполнено, пузырёк уровня останется на средине. При уходе пузырька уровня – одну половину отклонения от середины исправляют вращением подъёмных винтов (в любом порядке), а другую половину – исправительными винтами уровня. Эти действия повторяют до выполнения условия.

2 – я поверка.

Визирная ось трубы должна быть параллельна оси цилиндрического уровня ( VV_{1 ┴} UU₁ ). ( Главное условие).

Это условие выполняют двойным нивелированием способом «вперёд». Для этого закрепляют колышками линию АВ (рис.34) длиной 50-60 м. Нивелир устанавливают так, чтобы окуляр зрительной трубы находился над точкой А, и измеряют высоту прибора i ₁ . Элевационным винтом тщательно приводят пузырёк цилиндрического уровня в нуль-пункт и берут отсчёт по рейке, установленной на точке В. Если визирная ось не параллельна оси уровня I₁М₁, то вместо точки М₁ возьмём отсчёт b₁ в точке N₁.

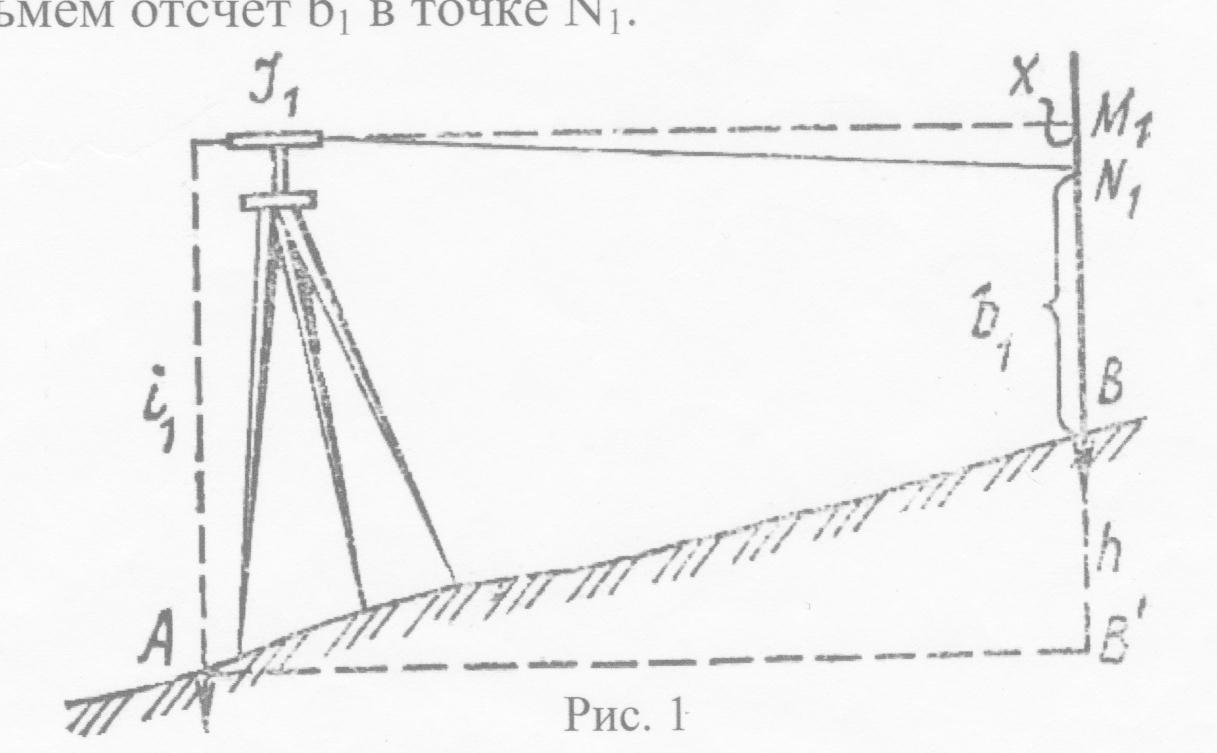
Рис.34

Затем нивелир и рейку меняют местами (рис.35), измеряют высоту прибора i₂ и берут отсчёт b₂ по рейке в точке А.

Величину Х, полученную влиянием не параллельности визирной оси и оси уровня, вычисляют по формуле:

Х = 0,5 ( i₁ + i₂ ) – 0,5 ( b₁ + b₂)

Если Х по абсолютной величине не превышает 4 мм, условие считают выполненным. Если условие нарушено, вычисляют правильный отсчёт по рейке – b_О. Как следует из рисунка 15, этот отсчёт равен:

b_О = b₂ + Х

Для юстировки, элевационным винтом, наводят среднюю нить на этот отсчёт. Исправительными винтами цилиндрического уровня приводят пузырёк уровня в нуль-пункт. После юстировки поверку повторяют до полного выполнения условия:

Х ≤ | 4 мм |.

I

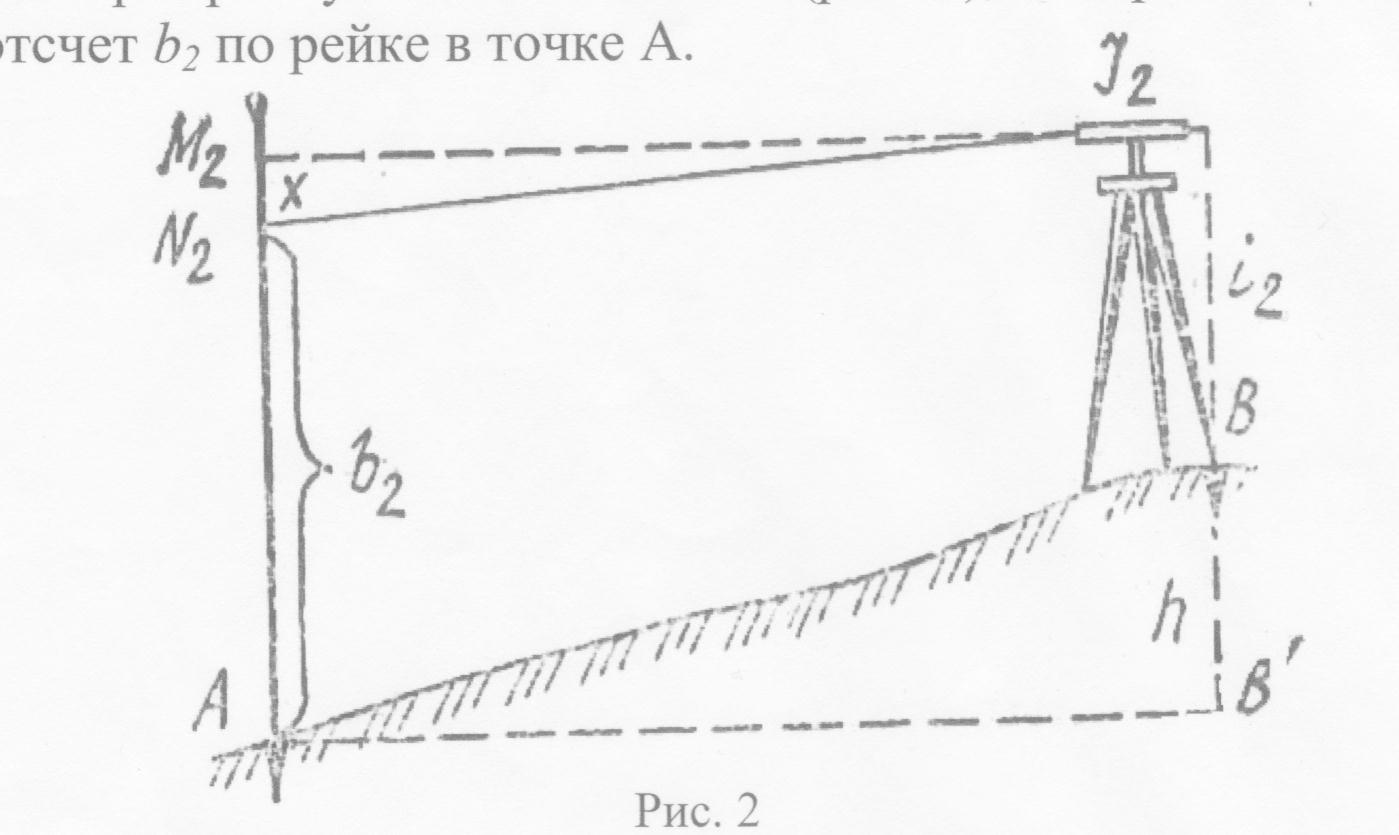
Рис.35

3 – я поверка.

Горизонтальная нить сетки должна быть перпендикулярна основной оси нивелира .

По круглому уровню приводят основную ось нивелира в отвесное положение. Замечают какую-либо точку на средней линии сетки нитей в одном из углов поля зрения трубы и поворачивают верхнюю часть прибора по азимуту. Если наблюдаемая точка в противоположном углу поля зрения трубы не сошла с нити, условие выполнено. Если условие нарушено, ослабляют крепёжные винты и пластину с сеткой нитей поворачивают до совмещения с траекторией движения наблюдаемой точки.

Тема: «Технология нивелирования. Вычислительная обработка результатов нивелирования».

В практике встречаются два основных вида геометрического нивелирования: продольное, когда нивелирование ведётся по направлению какой-либо трассы местности, и нивелирование площадей, выполняемое в основном для топографической съёмки.

В соответствии с заданной точностью, видом нивелирования, типом прибора и рее к будет изменяться порядок нивелирных работ. Независимо от названных условий должны соблюдаться общие условия нивелирования.

Станции выбираются так, чтобы обеспечивалась хорошая видимость на рейки, и чтобы визирный луч проходил выше поверхности земли не менее чем на 30 см. Расстояния от обеих реек до прибора должны быть по возможности одинаковые.

Нивелирование начинают с репера или с точки, отметка которой известна. Нивелир размещают примерно посередине между точками. На начальной и определяемой точках устанавливают рейки.

При взятии отсчётов по рейке нужно придерживаться следующего правила:

В момент взятия отсчёта по рейке, концы контактного уровня должны быть совмещены.

Порядок нивелирования на станции.

1. С помощью подъёмных винтов, пузырёк круглого уровня выводят в нульпункт.

2. Наводят трубу нивелира на заднюю рейку и при помощи фокусирования добиваются её чёткого изображения.

3. Пользуясь элевационным винтом, совмещают изображение концов пузырька контактного уровня и берут отсчёт по чёрной стороне рейки. Результаты записывают в журнал нивелирования.

4. Наводят трубу на переднюю точку (совмещают концы контактного уровня) и берут отсчёт по чёрной стороне рейки. Результаты записывают в журнал нивелирования.

5. Вычисляют превышение.

6. Поворачивают переднюю рейку красной стороной (совмещают концы контактного уровня) и берут отсчёт. Результаты записывают в журнал нивелирования.

7. Наводят трубу на заднюю точку (совмещают концы контактного уровня) и берут отсчёт по красной стороне рейки. Результаты записывают в журнал нивелирования.

8. Вычисляют превышение.

9. Устанавливают рейки на промежуточные точки и делают отсчёты по чёрной стороне рейки.

Расхождения в превышениях, вычисленных по чёрной и красной сторонам реек, не должны отличаться более чем на 4 мм. Если это условие выполнено, вычисляют среднее превышение. После контроля наблюдений на одной станции, переходят на другую станцию и проводят наблюдения в той же последовательности.

Образец записей и вычислений приведён в таблице 4.

Предварительная обработка результатов нивелирования заключается в постраничном контроле:

1. Подсчитывается сумма отсчётов по задней рейке – Σа и передней рейке – Σв.

Σа = 24355, Σв = 31362.

Так как суммы отсчётов по рейкам берутся по чёрной и красной сторонам, все значения делятся пополам.

= = – = – 3504

2. Подсчитывается сумма вычисленных превышений – Σh_выч. = – 7007.

= = – 3504

3. Подсчитывается сумма средних превышений – Σh_ср. = – 3504

Таблица 4.

№ станций	№ пикетов	Отсчёты по рейке, мм			Превышения, мм			Горизонт инструмента, м		Абсолютная отметка, м
		задний	передний	промежуточный		вычисленные	средние
1	Rр	1415 (1)									92,274
		6101 (4)				+1200 (5)
	0		0215 (2)			+1198 (6)	+1199 (7)
			4903 (3)								93,473
2	0	0596							94,069		93,473
		5283				– 1313
	+65			0085		– 1312	– 1313				93,984
	1		1909								92,160
			6595
3	1	0265									92,160
		4952				– 2207
	2		2472			– 2207	– 2207				89,953
			7159
4	2	0528									89,953
		5215				– 1183
	3		1711			– 1183	– 1183				88,770
			6398
Σ		24355	31362			– 7007	– 3504
Σа – Σв = 24355 – 31362 = – 7007 Σh = – 7007

Тема: «Назначение и виды геодезических

съёмок. Плановые и высотные сети».

Для составления планов и карт, решения различных геодезических задач, в том числе геодезического обеспечения строительства, на поверхности Земли располагают ряд точек, связанных между собой единой системой координат.

Совокупность закрепляемых на местности или зданиях точек, положение которых определено в единой системе координат, называют геодезическими сетями.

Геодезические сети подразделяются на плановые и высотные. Плановые служат для определения координат Х и У геодезических пунктов, высотные – для определения их высот Н.

Основными методами определения координат точек государственной сети являются:

1. Метод триангуляции;

2. Метод трилатерации;

3. Метод полигонометрии.

Определение высот точек производится нивелированием.

Плановые сети на местности строятся в виде геометрических фигур: треугольников, четырёхугольников, ломаных линий. При этом некоторые углы и стороны измеряются, а все остальные вычисляются. Для вычисления плановых координат вершин выбранных точек кроме элементов геометрических фигур необходимо знать ещё дирекционный угол стороны одной из фигур и координаты одной из вершин. Геодезические сети подразделяются на четыре вида: государственные, сгущения, съёмочные и специальные. Государственные геодезические сети – ГГС служат основой для создания всех остальных видов сетей.

Началом единого отсчёта плановых координат в России служит центр круглого зала Пулковской обсерватории в Санкт-Петербурге.

Государственные плановые геодезические сети являются главной геодезической основой топографических съёмок всех масштабов и подразделяются на четыре класса. Сеть первого класса имеет наибольшую точность и охватывает всю территорию страны. Сеть каждого последующего класса строится на основе сетей высших классов (рис.36). В настоящее время для построения государственных сетей используются спутниковые методы измерений.

Построение таких сетей предполагается осуществить в течение десяти ближайших лет.

Сети сгущения создаются для дальнейшего увеличения плотности государственных сетей. Плановые сети сгущения подразделяют на 1-й и 2-й разряды.

Съёмочные сети – это тоже сети сгущения, но с ещё большей плотностью. С точек съёмочных сетей производится съёмка предметов местности и рельефа для составления планов и карт различных масштабов.

Специальные геодезические сети создаются для геодезического обеспечения строительства сооружений.

Рис.36.

Государственная сеть триангуляции и полигонометрии.

Способ триангуляции состоит в том, что на местности строят сеть примыкающих друг к другу треугольников (рис.37), в которых измеряют все углы и хотя бы одну из сторон. Стороны остальных треугольников вычисляют по формулам тригонометрии. Решая прямую геодезическую задачу, определяют координаты опорных пунктов.

Способ трилатерации сводится к построению на местности смежных треугольников и геодезических четырёхугольников с измерением в каждом из них всех сторон и диагоналей.

Углы получают из тригонометрических вычислений, после чего определяют координаты опорных пунктов.

Рис.37. Сеть триангуляции.

Способ полигонометрии сводится к построению на местности ломаных линий с измерением сторон, углов поворота и примычных углов. По измеренным углам и сторонам, имея координаты исходной точки и дирекционный угол исходного направления, вычисляют координаты вершин полигона, которые являются опорными пунктами.

Государственные высотные геодезические сети создают для распространения по всей территории единой системы высот. За начало высот в России принят средний уровень Балтийского моря. Между пунктами государственных высотных геодезических сетей 1-го класса размещают пункты сетей 2-го, 3-го и т.д. классов. Для решения ограниченного круга вопросов при изысканиях, строительстве и эксплуатации зданий и сооружений создают высотную сеть технического класса. Нивелирные сети на строительных площадках создают на базе плановых сетей.

Тема: «Назначение и виды теодолитных

ходов. Состав полевых работ».

Для выноса проекта в натуру на строительной площадке создают геодезическую разбивочную опорную сеть (которая относится к специальным геодезическим сетям). Пункты опорной сети закрепляют постоянными знаками, сохраняют на весь период строительства и располагают таким образом, чтобы с них было удобно производить разбивочные работы. В строительной практике определение координат точек часто производится с помощью полигонометрии. Самый распространённый вид съёмочного планового обоснования – теодолитные ходы, опирающиеся на один или два исходных пункта.

Теодолитный ход – это система ломаных линий, углы между которыми измерены на местности теодолитом, а стороны мерным прибором.

Если теодолитный ход (полигон) опирается на один исходный пункт, он считается замкнутым; на два – разомкнутым. Разомкнутые теодолитные ходы используют в основном при строительстве сооружений линейного типа (ж/д., автодорог, трубопроводов, ЛЭП и т.д.). Замкнутые – при строительстве гражданских, общественных и производственных зданий.

Для ориентирования полигонов на местности и передачи координат на точки теодолитного хода производят его привязку к геодезическим пунктам более высокого класса. Привязка состоит в том, что определяется положение хотя бы одной точки относительно точек более высокого класса; измеряется между ними расстояние и примычный угол.

Плановая привязка – это передача координат и дирекционных углов с пунктов привязки на точки теодолитного хода.

Замкнутые теодолитные ходы создаются в виде многоугольников, в которых измеряются все внутренние углы и расстояния между точками (рис. 39). Разомкнутые теодолитные ходы создаются в виде ломаных линий (вдоль сооружений линейного типа), где измеряются правые или левые по ходу углы и расстояния между точками (рис. 38).

ΔI 1

Δ II 2 3 ΔIII

Рис. 38. ΔIV

I; II; III; IV – пункты государственной геодезической сети (твёрдые пункты);

1; 2; 3 – точки теодолитного хода;

γ₁ ; γ₂ – примычные углы;

β₁; β₂; β₃ – измеренные углы (левые);

А 1

D_В-1 β₂ D_1-2

γ₁

В 2

γ₂

D_4-В D_2-3

β₂

4 D_3-4 3

Рис. 39.

А; В – пункты государственной геодезической сети (твёрдые пункты);

1,2,3,4 – точки теодолитного хода;

γ₁ ; γ₂ – примычные углы;

β₁; β₂; β₃; β₄; β₅ – внутренние измеренные углы (правые по ходу лежащие);

D_В-1 ; D_4-В – расстояние между твёрдым пунктом и точками теодолитного хода;

D_1-2; D_2-3; D_3-4 – расстояния между точками теодолитного хода.

При строительстве зданий чаще используются замкнутые теодолитные ходы, поэтому будем рассматривать измерения и вычисления в этих ходах.

В замкнутых теодолитных ходах дирекционные углы сторон полигона вычисляются по формуле:

а) при внутренних измеренных углах вправо по ходу лежащих

α = α_n-1 + 180º - β_исп.

Дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180º и минус, исправленный горизонтальный угол вправо по ходу лежащий (рис.40).

с

1 α_1-2

5 2

4 3

Рис.40

б) при внутренних измеренных углах влево по ходу лежащих

α = α_n-1 + β_исп. - 180º

Дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс, исправленный горизонтальный угол влево по ходу лежащий и минус 180º (рисунок составьте самостоятельно).

Если при вычислении уменьшаемый угол окажется меньше вычитаемого, то к уменьшаемому прибавляется 360º. Если вычисленный дирекционный угол окажется больше 360º, то из него вычитают полный круг (360º).

В задачу теодолитной съёмки входит съёмка предметов местности (зданий, сооружений, отдельно стоящих деревьев и т.д.); контуров сельскохозяйственных и лесных угодий; путей сообщения; гидрографии (рек, озёр, болот).

Съёмка местности состоит из подготовительных, полевых и камеральных работ. К подготовительным относятся следующие работы:

• Выяснение необходимости съёмки и выбор её масштаба;

• Составление календарного плана и сметы на работы;

• Расчёт необходимого количества рабочих и транспорта;

• Составление списка на необходимые инструменты, оборудование, материалы.

К полевым работам при теодолитной съёмке относятся:

• Рекогносцировка участка местности;

• Закрепление знаками точек теодолитного хода;

• Измерение углов и сторон теодолитного хода;

• Привязка теодолитного хода к геодезическим пунктам более высокого класса.

Рекогносцировка участка, т.е. его обход и осмотр, производится для того, чтобы получить представление о размерах участка, сложности ситуации, условиях для измерения углов и линий и условиях привязки теодолитного хода к пунктам геодезической сети более высокого класса. В процессе рекогносцировки выбирают местоположение точек теодолитного хода таким образом, чтобы на привязку ситуации местности к вершинам и сторонам хода затрачивалось меньше труда и времени.

Вершины теодолитного хода закрепляют постоянными или временными знаками, в зависимости от места их нахождения и срока службы. В процессе закрепления составляют схему, на которой показывают расположение вершин и сторон хода относительно ситуации местности. Эта схема используется при выполнении работ по измерению углов и длин сторон теодолитного хода.

Углы между сторонами теодолитного хода измеряют теодолитом одним полным приёмом (при КП и КЛ). Расхождение значений в полуприёмах не должны превышать двойной точности (t) отсчитывания теодолита

|Δβ| 2t

Длины линий в ходах измеряют рулетками, мерными лентами, дальномерами оптическими и электронными, а также широко применяемые в настоящее время лазерными дальномерами. Каждую сторону измеряют дважды в прямом и обратном направлениях. Расхождения в измеренных значениях не должны превышать от измеряемой длины линии

|Δl |

При съёмке составляется абрис, в котором схематически зарисовывают ситуацию местности, показывают все снимаемые точки, записывают результаты всех выполняемых угловых и линейных измерений. Абрис составляется отдельно для каждой стороны теодолитного хода (рис.41).

Полевым контролем измерения внутренних углов в полигоне будет сумма всех углов – Ʃβ_изм. Из математики известно, что сумма внутренних углов в многоугольнике определяется по формуле:

Ʃβ_теор. = 180º · (n – 2), где

n – число углов в многоугольнике.

Результаты, полученные при измерениях, содержат в себе ошибки. Разность между измеренной и теоретической суммой называется невязкой и обозначается – ƒ. Следовательно, угловая невязка – ƒ_β будет равняться разности между измеренной и теоретической суммой, т.е.

ƒ_β = Ʃβ_изм. – Ʃβ_теор.

Полученная угловая невязка сравнивается с допустимой:

ƒ_{β доп.} = 1ʹ· t · , где

t – точность теодолита;

n – число углов в полигоне.

Установив, что угловая невязка не превышает допустимого предела, а длины линий измерены с точностью не больше , приступают к камеральной обработке теодолитного хода.

Рис. 41.

Тема: «Камеральная обработка

теодолитного хода».

После выполнения полевых работ производится камеральная обработка результатов измерений. Камеральная обработка начинается с тщательной проверки всех записей и вычислений в полевых журналах. По измеренным значениям горизонтальных углов и горизонтальным проложениям производится вычисление координат точек теодолитного хода, путём решения прямой геодезической задачи. По вычисленным координатам строится план теодолитного хода, на котором выполняется плановая привязка здания, путём решения обратной геодезической задачи.

Вычислительная обработка теодолитного хода ведётся по этапам:

1. Контроль угловых измерений.

2. Уравнивание углов.

3. Контроль линейных измерений.

4. Уравнивание приращений координат.

5. Вычисление координат точек.

I этап - Контроль угловых измерений.

1. Вычисляется сумма измеренных углов в полигоне – Σβ_изм.

2. Вычисляется теоретическая сумма углов в замкнутом полигоне

Σβ_теор. = 180º · (n – 2), где

n – число углов в полигоне.

3. Вычисляется угловая невязка в полигоне – ƒ_β, которая получается в результате погрешности при измерении горизонтальных углов

ƒ_β = Σβ_изм. – Σβ_теор.

4. Вычисляется допустимая угловая невязка

ƒ_{β доп.} = 2 t , где

t – точность теодолита

n – число углов в полигоне.

II этап- Уравнивание углов.

5. Если ƒ_β ƒ_{β доп.}, то её распределяют с обратным знаком на все углы поровну

δ_β =

6. Вычисляются исправленные значения с учётом поправок

β = β_изм. δ

Сумма исправленных углов должна равняться теоретической сумме

Σβ = Σβ_теор.

7. По исходному дирекционному углу и исправленным значениям углов вычисляются дирекционные углы последующих сторон

α_n = α_n-1 + 180º - β_n

контролем вычислений является получение исходного дирекционного угла.

8. По вычисленным дирекционным углам, определяются румбы и их названия, используя формулы зависимости между дирекционными углами и румбами.

III этап- Контроль линейных измерений.

9. Вычисляется периметр теодолитного хода – Р.

10. По румбам и горизонтальным проложениям сторон полигона вычисляются приращения координат

Х = d · cos r

У = d · sin r

Знаки приращений координат зависят от направления линий, т.е. от названия румбов линий.

11. Вычисляются невязки в приращениях координат

ƒ_Х = Σ Х

ƒ_У = Σ У

12. Вычисляется абсолютная линейная невязка

ƒ_абс. =

13. Вычисляется относительная линейная невязка

ƒ_отн. =

14. Полученную относительную невязку сравнивают с допустимой

ƒ_доп. =

если ƒ_отн. ƒ_доп., то вычисленные невязки в приращениях координат распределяются с обратным знаком пропорционально длинам сторон.

IV этап- Уравнивание приращений координат.

15. Вычисляются поправки в приращения координат

δ_Х = · d

δ_У = · d

64

16. Вычисляются исправленные приращения координат

_испр. = δ

_испр. = δ

17. Вычисляется сумма исправленных приращений

Σ _испр. = 0

Σ _испр. = 0