
- •Вопросы к экзамену
- •1. Неопределенный интеграл
- •2. Определенный интеграл
- •Производная интеграла по переменному верхнему пределу
- •Формула Ньютона – Лейбница
- •Замена переменной и интегрирование по частям
- •3. Приложения определенного интеграла. Несобственные Интегралы
- •Формула площадей
- •Полярные координаты [править]
- •Площадь поверхности [править]
- •Объем тела вращения Вращение по оси X [править]
- •Вращение по оси y [править]
- •Формула объемов
- •Длина плоской кривой (длина графика функции)
- •6.)Несобственные интегралы. Сходимость. Признак сравнения
- •Абсолютная сходимость [править]
- •Условная сходимость [править]
- •4. Функции многих переменных (1) Дифференцируемость функции двух переменных, полный дифферен- циал.
- •Полный дифференциал
- •(3) Производная неявно заданной функции
- •(4) Производная по направлению и градиент
- •(5) Градиент и линии уровня. Уравнение касательной к линии уровня
- •(6) Градиент функции трех переменных. Уравнение касательной плоскости к поверхности уровня
- •(9)(10) Экстремум функции двух переменных. Первое необходимое условие экстремума
- •(11) Достаточное условие экстремума функции двух переменных
- •5. Ряды
- •Понятие числового положительного ряда
- •Признаки сравнения для положительных числовых рядов
- •4)Обобщенный гармонический ряд
- •Знакопеременный ряд Править
- •Абсолютная сходимость
- •Признаки абсолютной сходимости[править] Признак сравнения[править]
- •Признак сходимости рядов с монотонно убывающими членами[править]
- •Признак Лейбница сходимости знакочередующегося ряда
- •Свойства степенных рядов (без доказательства)
- •Ряд Тейлора (вывод разложения)
- •Разложение e X, cosx, sinx в ряд Тейлора
- •6.Комплексные числа
- •Алгебраическая форма
- •Тригонометрическая форма
- •7. Дифференциальные уравнения
- •Метод последовательных приближений [править]
- •4)Линейный дифференциальный оператор и его свойства
- •4)Свойства решений однородного уравнения
5. Ряды
(1) Признак сравнения рядов с положительными членами
Понятие числового положительного ряда
В общем
виде положительный
числовой ряд можно
записать так: ![]() .
Здесь:
.
Здесь:
![]() –
математический значок суммы;
–
математический значок суммы;
![]() – общий
член ряда (запомните
этот простой термин);
– общий
член ряда (запомните
этот простой термин);
![]() –
переменная-«счётчик». Запись
–
переменная-«счётчик». Запись ![]() обозначает,
что проводится суммирование от 1 до
«плюс бесконечности», то есть, сначала
у нас
обозначает,
что проводится суммирование от 1 до
«плюс бесконечности», то есть, сначала
у нас ![]() ,
затем
,
затем ![]() ,
потом
,
потом ![]() ,
и так далее – до бесконечности. Вместо
переменной
иногда
используется переменная
,
и так далее – до бесконечности. Вместо
переменной
иногда
используется переменная ![]() или
или ![]() .
Суммирование не обязательно начинается
с единицы, в ряде случаев оно может
начинаться с нуля
.
Суммирование не обязательно начинается
с единицы, в ряде случаев оно может
начинаться с нуля ![]() ,
с двойки
,
с двойки ![]() либо
с любого натурального
числа.
либо
с любого натурального
числа.
В соответствии
с переменной-«счётчиком» любой ряд
можно расписать развёрнуто:
![]() –
и так далее, до бесконечности.
–
и так далее, до бесконечности.
Будем
считать, что ВСЕ слагаемые ![]() –
это неотрицательные
ЧИСЛА.
То есть, на данном уроке речь пойдет
о положительных
числовых рядах.
–
это неотрицательные
ЧИСЛА.
То есть, на данном уроке речь пойдет
о положительных
числовых рядах.
Признаки сравнения для положительных числовых рядов
Существуют два признака сравнения, один из них я буду называть просто признаком сравнения, другой – предельным признаком сравнения.
Сначала рассмотрим признак сравнения. На практике он встречается довольно редко, но эта статья была бы неполной без данной информации.
Признак
сравнения: Рассмотрим
два положительных числовых ряда
и ![]() . Если
известно,
что ряд
– сходится,
и выполнено неравенство
. Если
известно,
что ряд
– сходится,
и выполнено неравенство ![]() (для
(для ![]() ),
то ряд
тоже
сходится.
),
то ряд
тоже
сходится.
Иными словами: Из сходимости ряда с бОльшими членами следует сходимость ряда с меньшими членами.
Исследовать
ряд на сходимость ![]()
Заглядываем
в «пачку» обобщенного гармонического
ряда и находим похожий ряд: ![]() .
Из теории известно, что он сходится.
Теперь нам нужно показать, что всех
значений
справедливо
неравенство
.
Из теории известно, что он сходится.
Теперь нам нужно показать, что всех
значений
справедливо
неравенство ![]() .
.
Если
,
то ![]() Если
,
то
Если
,
то ![]() Если
,
то
Если
,
то ![]() Если
Если ![]() ,
то
,
то ![]() ….
И
так далее.
….
И
так далее.
Оформить решение можно так: “ Сравним исследуемый ряд со сходящимся рядом . Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство , значит, по признаку сравнения исследуемый ряд сходится вместе с рядом . ” В принципе, можно расписать и подробнее, указав, что неравенство выполняется для нескольких первых членов.
Проанализируем
признак сравнения и решенный пример с
неформальной точки зрения. Все-таки,
почему ряд
сходится?
А вот почему. В теории доказано, что
ряд
сходится,
значит, он имеет некоторую конечную сумму ![]() :
: ![]() .
Если все члены ряда
меньше соответствующих
членов ряда
,
то ясен пень, что сумма ряда
не
может быть больше числа
,
и тем более, не может равняться
бесконечности!
.
Если все члены ряда
меньше соответствующих
членов ряда
,
то ясен пень, что сумма ряда
не
может быть больше числа
,
и тем более, не может равняться
бесконечности!
Аналогично
можно доказать сходимость «похожих»
рядов: ![]() ,
, ![]() ,
, ![]() и
т.д.
и
т.д.
!
Обратите внимание,
что во всех случаях в знаменателях у
нас находятся «плюсы». Если есть минусы,
то рассматриваемый признак
сравнения может не дать результата.
Например, рассмотрим ряд ![]() .
Попробуйте аналогично сравнить его со
сходящимся рядом
.
Попробуйте аналогично сравнить его со
сходящимся рядом ![]() ,
выпишите несколько неравенств для
первых членов. Вы увидите, что
неравенство
не
выполняется и
признак не дает нам ответа.
Придется использовать другой признак,
чтобы выяснить, сходится этот ряд или
нет.
,
выпишите несколько неравенств для
первых членов. Вы увидите, что
неравенство
не
выполняется и
признак не дает нам ответа.
Придется использовать другой признак,
чтобы выяснить, сходится этот ряд или
нет.
(2) Признак Даламбера
При́знак д’Аламбе́ра (или Признак Даламбера) — признак сходимости числовых рядов, установлен Жаном д’Аламбером в 1768 г.
Если для числового ряда
![]()
существует
такое число ![]() ,
, ![]() ,
что начиная с некоторого номера
выполняется неравенство
,
что начиная с некоторого номера
выполняется неравенство
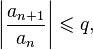
то данный ряд абсолютно сходится; если же, начиная с некоторого номера
![]()
то ряд расходится.
Признак сходимости д’Аламбера в предельной форме [править]
Если существует предел
![]()
то
рассматриваемый ряд абсолютно сходится
если ![]() ,
а если
,
а если ![]() —
расходится.
—
расходится.
Замечание. Если ![]() ,
то признак д′Аламбера не даёт ответа
на вопрос о сходимости ряда.
,
то признак д′Аламбера не даёт ответа
на вопрос о сходимости ряда.
Доказательство [править]
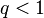 ,
тогда существует
,
тогда существует 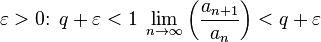 ,
существует
,
существует 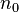 ,
для любого
,
для любого 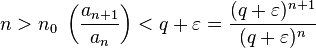 .
Ряд
из
.
Ряд
из 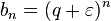 сходится
(как геометрическая прогрессия). Значит,
ряд из
сходится
(как геометрическая прогрессия). Значит,
ряд из 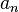 сходится
(по признаку сравнения).
сходится
(по признаку сравнения).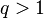 ,
тогда существует
,
тогда существует 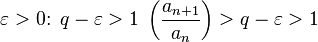 .
. 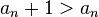 для
любого
для
любого 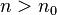 .
Тогда
не
стремится к нулю и ряд расходится.
.
Тогда
не
стремится к нулю и ряд расходится.
(3) Интегральный признак Коши
Интегральный
признак Коши́-Макло́рена —
признак сходимости убывающего
положительного числового
ряда.
Признак Коши-Маклорена даёт возможность
свести проверку сходимости ряда к
проверке сходимости несобственного
интеграла соответствующей
функции на ![]() ,
последний часто может быть найден в
явном виде.
,
последний часто может быть найден в
явном виде.
Формулировка теоремы [править]
-
Пусть для функции f(x) выполняется:
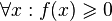 (функция
принимает неотрицательные значения)
(функция
принимает неотрицательные значения)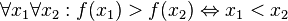 (функция
монотонно убывает)
(функция
монотонно убывает)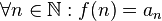 (соответствие
функции ряду)
(соответствие
функции ряду)
Тогда ряд
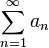 и
несобственный интеграл
и
несобственный интеграл  сходятся
или расходятся одновременно.
сходятся
или расходятся одновременно.
Набросок доказательства [править]
Набросок доказательства [править]
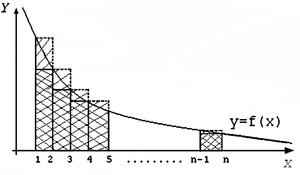
Построим на графике f(x) ступенчатые фигуры как показано на рисунке
Площадь большей фигуры равна
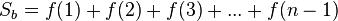
Площадь меньшей фигуры равна
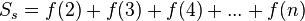
Площадь криволинейной трапеции под графиком функции равна
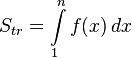
Получаем
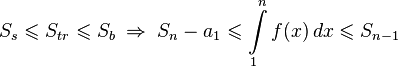
Далее доказывается с помощью критерия сходимости знакоположительных рядов.
Примеры [править]
 расходится
так как
расходится
так как 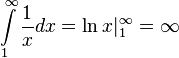 .
. сходится
так как
сходится
так как 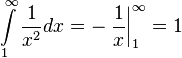 .
.
Оценка остатка ряда [править]
Интегральный
признак Коши позволяет
оценить остаток ![]() знакоположительного
ряда. Из полученного в доказательстве
выражения
знакоположительного
ряда. Из полученного в доказательстве
выражения
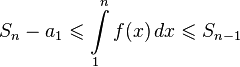
с помощью несложных преобразований получаем:
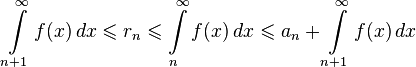 .
.
