
- •Вопросы к экзамену
- •1. Неопределенный интеграл
- •2. Определенный интеграл
- •Производная интеграла по переменному верхнему пределу
- •Формула Ньютона – Лейбница
- •Замена переменной и интегрирование по частям
- •3. Приложения определенного интеграла. Несобственные Интегралы
- •Формула площадей
- •Полярные координаты [править]
- •Площадь поверхности [править]
- •Объем тела вращения Вращение по оси X [править]
- •Вращение по оси y [править]
- •Формула объемов
- •Длина плоской кривой (длина графика функции)
- •6.)Несобственные интегралы. Сходимость. Признак сравнения
- •Абсолютная сходимость [править]
- •Условная сходимость [править]
- •4. Функции многих переменных (1) Дифференцируемость функции двух переменных, полный дифферен- циал.
- •Полный дифференциал
- •(3) Производная неявно заданной функции
- •(4) Производная по направлению и градиент
- •(5) Градиент и линии уровня. Уравнение касательной к линии уровня
- •(6) Градиент функции трех переменных. Уравнение касательной плоскости к поверхности уровня
- •(9)(10) Экстремум функции двух переменных. Первое необходимое условие экстремума
- •(11) Достаточное условие экстремума функции двух переменных
- •5. Ряды
- •Понятие числового положительного ряда
- •Признаки сравнения для положительных числовых рядов
- •4)Обобщенный гармонический ряд
- •Знакопеременный ряд Править
- •Абсолютная сходимость
- •Признаки абсолютной сходимости[править] Признак сравнения[править]
- •Признак сходимости рядов с монотонно убывающими членами[править]
- •Признак Лейбница сходимости знакочередующегося ряда
- •Свойства степенных рядов (без доказательства)
- •Ряд Тейлора (вывод разложения)
- •Разложение e X, cosx, sinx в ряд Тейлора
- •6.Комплексные числа
- •Алгебраическая форма
- •Тригонометрическая форма
- •7. Дифференциальные уравнения
- •Метод последовательных приближений [править]
- •4)Линейный дифференциальный оператор и его свойства
- •4)Свойства решений однородного уравнения
(9)(10) Экстремум функции двух переменных. Первое необходимое условие экстремума
Положим, что имеется некоторая функция с двумя переменными
Определение: Точка называется точкой экстремума (максимума или минимума)
функции , если есть соответственно наибольшее или наименьшее значение функции в некоторой окрестности точки .
При этом значение называется экстремальным значением функции (соответственно максимальным или минимальным). Говорят также, что функция имеет в точкеэкстремум (или достигает в точке экстремума).
Теперь определим достаточные условия для экстремума функции двух переменных. Так же как и для функции одной переменной, необходимый признак экстремума в случае многих переменных не является достаточным. Это значит, что из равенства нулю частных производных в данной точке вовсе не следует, что эта точка обязательно является точкой экстремума. Возьмем функцию Ее частные производные равны нулю в начале координат, однако функция экстремума не достигает. В самом деле, функция , будучи равной нулю в начале координат, имеет в любой близости к началу координат как положительные значения (в первом и третьем координатных углах), так и отрицательные (во втором и четвертом координатных углах), и значит, нуль не является ни наибольшим, ни наименьшим значением этой функции.
Достаточные условия экстремума для функции нескольких переменных носят значительно более сложный характер, чем для функции одной переменной. Мы рассмотрим эти условия без доказательства только для функции двух переменных.
Пусть точка является стационарной точкой функции
, т. е.
Вычислим в точке значение вторых частных производных функции и обозначим их для краткости буквами A, B и C:
Если , то функция имеет в точке экстремум: при A<0 и C<0 и минимум при A>0 и C>0 (Из условия следует, что A и C обязательно имеют одинаковые знаки).
Если, то точка не является точкой экстремума.
Если, то неясно, является ли точка точкой экстремума и требуется дополнительное исследование.
(11) Достаточное условие экстремума функции двух переменных
Пусть функция
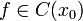 непрерывна
в
непрерывна
в 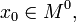 и
существуют конечные или бесконечные
односторонние производные
и
существуют конечные или бесконечные
односторонние производные 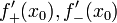 .
Тогда при условии
.
Тогда при условии
![]()
![]() является
точкой строгого локального максимума.
А если
является
точкой строгого локального максимума.
А если
![]()
то является точкой строгого локального минимума.
Заметим, что при этом функция не дифференцируема в точке
Пусть функция
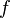 непрерывна
и дважды дифференцируема в точке
.
Тогда при условии
непрерывна
и дважды дифференцируема в точке
.
Тогда при условии
![]() и
и ![]()
является точкой локального максимума. А если
и ![]()
то является точкой локального минимума.
Пусть функция дифференцируема
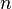 раз
в точке
и
раз
в точке
и 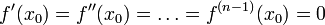 ,
а
,
а 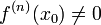 .
.
Если
чётно
и ![]() ,
то
-
точка локального максимума. Если
чётно
и
,
то
-
точка локального максимума. Если
чётно
и ![]() ,
то
-
точка локального минимума. Если
нечётно,
то экстремума нет.
,
то
-
точка локального минимума. Если
нечётно,
то экстремума нет.
(12) Условный экстремум. Метод множителей Лагранжа (простейший слу-
чай)
Пусть на открытом множестве G Rn заданы функции.
yi=fi(x) i=1,2,3,…,m (6.1)
x=(x1,x2,…,xn).Обозначим через Е множество точек x G , в которых все функции fii=1,2,3,…,m обращаются в нуль:
E={x: fi(x)=0, i=1,2,3,…,m, x G} (6.2)
Уравнения
fi(x)=0, i=1,2,3,…,n (6.3)
будем называть уравнениями связи.
Определение : пусть на множестве G задана функция y=f0(x) .Тогда x(0) E называется точкой условного экстремума (принят также термин “относительный экстремум”) функции f0(x) относительно (или при выполнении) уравнений связи (6.3) , если она является точкой обычного экстремума этой функции , рассмотриваемой только на множестве Е.
Составим функцию Лагранжа в виде линейной комбинации функции и функций
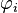 ,
взятых с коэффициентами,
называемыми множителями
Лагранжа —
,
взятых с коэффициентами,
называемыми множителями
Лагранжа — 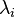 :
:
![]()
где ![]() .
.
Составим систему из
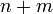 уравнений,
приравняв к нулю частные
производные функции
Лагранжа
уравнений,
приравняв к нулю частные
производные функции
Лагранжа 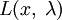 по
по 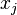 и
.
и
.Если полученная система имеет решение относительно параметров
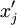 и
и 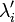 ,
тогда точка
,
тогда точка 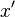 может
быть условным экстремумом, то есть
решением исходной задачи. Заметим, что
это условие носит необходимый, но не
достаточный характер.
может
быть условным экстремумом, то есть
решением исходной задачи. Заметим, что
это условие носит необходимый, но не
достаточный характер.
