(3) Производная неявно заданной функции
Функция вида 
называется
неявной. Дифференцируя обе части этого
тождества по х (пользуясь
правилом дифференцирования сложной
функции), считая, что y есть
функция от x ,
получим уравнение первой степени
относительно y' .
Из этого уравнения легко находят y' .
Пример. 
Решение: Дифференцируя
по 
обе
части уравнения, получим
;
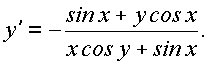
(4) Производная по направлению и градиент
Пусть в
некоторой области 
задана
функция 
и
точка 
.
Проведем из точки 
вектор 
,
направляющие косинусы которого 
.
На векторе
,
на расстоянии 
от
его начала рассмотрим точку 
,
т.е.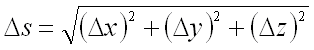 
.
Будем предполагать, что функция и ее частные производные первого порядка непрерывны в области .
Предел
отношения 
при 
называется производной
от функции
в
точке
по
направлению вектора
и
обозначается 
,
т.е.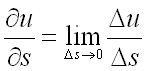
.
Для
нахождения производной от функции
в
заданной точке 
по
направлению вектора 
используют
формулу: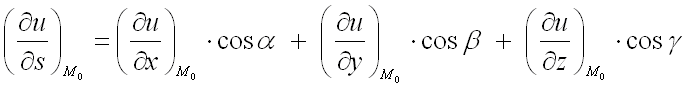 
,
где
–
направляющие косинусы вектора
,
которые вычисляются по формулам:
.
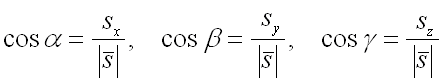Пусть
в каждой точке некоторой области
задана
функция
.
Вектор,
проекциями которого на оси координат
являются значения частных производных
этой функции в соответствующей точке,
называется градиентом
функции
и
обозначается 
или 
(читается
«набла у»):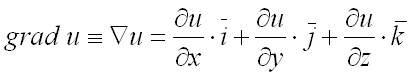 
.
При этом говорят, что в области определено векторное поле градиентов.
Для
нахождения градиента функции
в
заданной точке
используют
формулу:
.
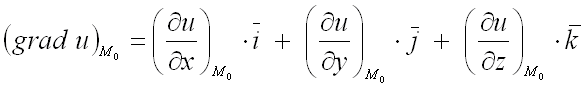Свойства градиента
1. Производная
в данной точке по направлению
вектора
имеет
наибольшее значение, если направление
вектора
совпадает
с направлением градиента. Это наибольшее
значение производной равно 
.
2. Производная по направлению вектора, перпендикулярного к вектору , равна нулю.
(5) Градиент и линии уровня. Уравнение касательной к линии уровня
Определение. Градиентом Функции Z=F(M)
в точке М(х; у) называется вектор,
координаты которого равны соответствующим
частным производным 
и
,
взятым в точке М(х; у).
Обозначение. 
Определение. Линией уровня функции U=F(X, Y) называется линия F(X, Y)=С на плоскости XOy, в точках которой функция сохраняет постоянное значение U=C.
Линии уровня геометрически изображаются на плоскости изменения независимых переменных в виде кривых линий. Получение линий уровня можно представить себе следующим образом. Рассмотрим множество С, которое состоит из точек трехмерного пространства с координатами (X, Y, F(X, Y)=Const), которые, с одной стороны, принадлежат графику функции Z=F(X, Y), с другой - лежат в плоскости, параллельной координатной плоскости ХОУ, и отстоящей от неё на величину, равную заданной константе. Тогда для построения линии уровня достаточно поверхность графика функции пересечь плоскостью Z=Const и линию пересечения спроектировать на плоскость ХОУ. Проведенное рассуждение является обоснованием возможности непосредственно строить линии уровня на плоскости ХОУ.
Линия уровня - это линия в плоскости ху, которая задается уравнением y^2-4y+x+2 = С, где С -произвольная константа. Каждому значению С соответствует своя линия уровня. ЧТобы линия уровня проходила через точку А(1,1), надо подставить координаты этой точки в уравнение: 1^2-4+1+2=С, т.е. С=0. Значит линия уровня заданной функции z=y^2-4y+x+2, которая проходит через точку А(1,1), задается уравнением y^2-4y+x+2=0. Уравнение ее касательной в точке А(1,1) имеет вид (уравнение касательной для неявно заданной кривой): -2(у-1)+(х-1)=0, т.е. х=2у-1. Ответ: х=2у-1