6.)Несобственные интегралы. Сходимость. Признак сравнения

Пусть функция f(x) определена на полуоси   и интегрируема по любому отрезку [a,b], принадлежащему этой полуоси. Предел интеграла 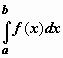  при   называется несобственным интегралом функции f(x) от a до   и обозначается  .  Итак, по определению, 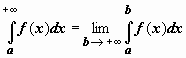 . Если этот предел существует и конечен, интеграл   называется сходящимся; если предел не существует или бесконечен, интеграл называется расходящимся. 

Абсолютная сходимость [править]

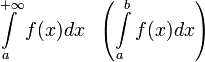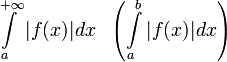Интеграл   называется абсолютно сходящимся, если  сходится. Если интеграл сходится абсолютно, то он сходится.

Условная сходимость [править]

Интеграл 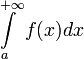  называется условно сходящимся, если   сходится, а 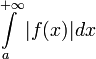  расходится.

Признаки сравнения

 Признаки сравнения

     1. Если две функции f(x) и φ(x) для всех значений x из полуотрезка [a, +∞] не принимают отрицательных значений и к тому же

f(x) ≤ φ(x)     (6)

то   сходится, если сходится интеграл  , и   расходится, если расходится  .

     2. Если x → +∞

     (7)

причем c > 0, c ≠ ∞ и f(x) ≠ 0 для всех достаточно больших x, то интегралы   и   либо оба сходятся, либо оба расходятся.

     3. Если сходится  , то сходится и  , где k - величина постоянная.

     Эти признаки распространяются и на интегралы вида  , но относятся только к указанным выше функциям.

     4. Для решения вопроса о сходимости интеграла   в том случае, когда функция f(x) является знакопеременной в промежутке [a, +∞], можно применить такую теорему:

     Если несобственный интеграл   от абсолютной величины функции f(x) сходится, то сходится и интеграл  .

4. Функции многих переменных (1) Дифференцируемость функции двух переменных, полный дифферен- циал.

Пусть функция z=f(x, y) определена в некоторой области D на плоскости xOy. Возьмем

точку (x, y)∈D и выбранным значениям x и y дадим любые приращения ∆x и ∆y, но такие,

чтобы точка (x+∆x, y+∆y)∈D.

Определение. Функция z=f(x, y) называется дифференцируемой в точке (x, y)∈D, если

полное приращение ∆x=f(x+∆x, y+∆y)-f(x,y) этой функции, отвечающее приращениям ∆x,

∆y аргументов, можно представить в виде

∆z=A∆x+B∆y+α(∆x, ∆y)∆x+β(∆x, ∆y)∆y (1),

где A и B не зависят от ∆x и ∆y (но вообще зависят от x и y), а α(∆x, ∆y) и β(∆x, ∆y)

стремятся к нулю при стремлении к нулю ∆x и ∆y.

Если функция z=f(x, y) дифференцируема в точке (x, y), то часть A∆x+B∆y приращения

функции, линейная относительно ∆x и ∆y, называется полным дифференциалом этой

функции в точке (x, y) и обозначается символом dz:

dz=A∆x+β∆y (2)

Таким образом, ∆z=dz+α⋅∆ x+β⋅∆ y

Полный дифференциал

Полный дифференциал, функции f (x, у, z,...) нескольких независимых переменных — выражение

 ,

в случае, когда оно отличается от полного приращения

Df = f (x + Dx, y + Dy, z + Dz,…) - f (x, y, z, …)

на величину, бесконечно малую по сравнению с

(2) Производная сложной функции (цепное правило)

"Двухслойная" сложная функция записывается в виде где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.  Если f и g - дифференцируемые функции, то сложная функция   также дифференцируема по x и ее производная равна Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!  Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.  Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".

Пример 1

Найти производную функции  . Решение. Поскольку  , то по правилу производной сложной функции получаем