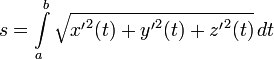4. Замена переменной и интегрирование по частям

Теорема 17.4. Если выполнены условия: 1) функция /(х) непрерывна на отрезке [а, Ь\, 2) отрезок [а, Ь\ является множеством значений функции х = ф(/), определенной на отрезке а < / < р и имеющей на нем непрерывную производную: 3) ф (а) = а, ф (р) = Ь, то справедлива формула

Теорема 17.5. Если функции Имеют непрерывные про

Изводные на отрезке , то справедлива формула

(

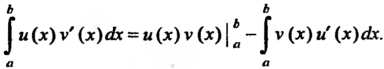3. Приложения определенного интеграла. Несобственные Интегралы

1. Формула площадей

Площадь, заключённая между графиком непрерывной функции на интервале   и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:

Площадь, заключённая между графиками двух непрерывных функций   на интервале   находится как разность определённых интегралов от этих функций:

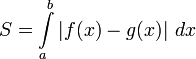
Полярные координаты [править]

В полярных координатах: площадь, ограниченная графиком функции   и лучами   вычисляется по формуле:

.

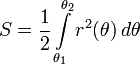Площадь поверхности [править]

Основная статья: Площадь поверхности

Для определения площади кусочно гладкой поверхности в трёхмерном пространстве используют ортогональные проекции к касательным плоскостям в каждой точке, после чего выполняют предельный переход. В результате, площадь искривлённой поверхности A, заданной вектор-функцией  , даётся двойным интегралом^[1]:

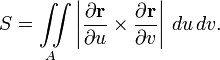
2. Объем тела вращения Вращение по оси X [править]

Объём тела, образуемого вращением вокруг оси   фигуры, ограниченной функцией   на интервале  , осью   и прямыми   и   равен:

Вращение по оси y [править]

Объём тела, образуемого вращением вокруг оси   фигуры, ограниченной функцией   на интервале  , осью   и прямыми   и   равен:

Альтернативные формулы вычисления  :

 и 

3. Формула объемов

V =a³

Формула объема куба

Формула объема призмы V =S_oh

Формула объема параллелепипеда V =S_o минус h

Формула объема прямоугольного параллелепипеда V =a b h

Формула объема пирамиды

V =	1	So - h
	3

Формула объема правильного тетраэдра

V=	a3√2
	12

Формулы объема цилиндра

• V = π R² h

• V = S_o h

Формулы объема конуса

V =	1	π R2 h
	3

V =	1	Soh
	3

Формула объема шара

V =	4	π R3
	3

4. Длина плоской кривой (длина графика функции)

Чтобы вычислить длину отрезка кривой, вновь представим ее себе как ломаную с бесконечно малыми звеньями ds. Когда точка (x,y) движется вдоль одного звена, ее координата xувеличивается на dx, а y -- на dy, причем мы уже знаем как найти связь этих дифференциалов. Остается заметить, что по теореме Пифагора ds² = dx² + dy², и что длина всего отрезка кривой равна сумме длин звеньев ломаной, т.е.

.

Напр., длина половины единичной окружности, обозначаемая как π, есть длина дуги кривой, заданной уравнением x² + y² = 1 при x = − 1..1 и  . Связь дифференциалов дается равенством xdx + ydy = 0, поэтому

.

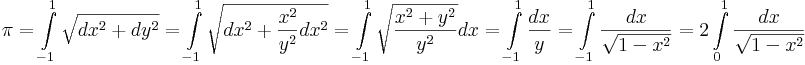Эту формулу можно проверить, сравнив измеренную длину полуокружности и ту, что получается, если в этой "сумме" взять dx малым но конечным. Напр., если отрезок x = 0..1 делится всего на N частей, то dx = 1 / N и

.

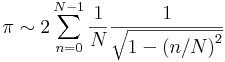При N = 10⁵ эта формула дает вполне нормальный результат 3.135. На самом деле, формула плоха из-за того, что знаменатель обращается на одном из концов отрезка в нуль.

(5) Длина кривой, заданной параметрически (на плоскости и в пространстве)

Пусть непрерывная кривая   задана параметрически:

,

(1)

где  . Рассмотрим всевозможные разбиения интервала значений параметра   на   отрезков:  . Соединив точки кривой   отрезками прямых, мы получим ломаную линию. Тогда длина отрезка кривой определяется как точная верхняя грань суммарных длин всех таких ломаных.

Всякая непрерывная кривая имеет длину, конечную или бесконечную. Если все функции в (1) являются функциями ограниченной вариации, то длина кривой существует и конечна. В математическом анализе выводится формула для вычисления длины   отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:

(2)

Формула подразумевает, что   и длина отсчитывается в сторону возрастания параметра t. Если рассматриваются два разных направления отсчёта длины от точки кривой, то часто удобно приписать дуге на одном из этих направлений знак минус.

В n-мерном случае вместо (2) имеем аналогичную формулу:

.

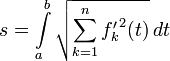Можно также вычислить длину кривой   через криволинейный интеграл I рода: