Метод последовательных приближений [править]
Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:
Это условие необходимо для сходимости ряда Лиувилля — Неймана:
который
и является решением уравнения. 
— 
-ая
степень интегрального оператора 
:
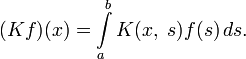
Впрочем,
такое решение является хорошим
приближением лишь при достаточно
малых 
.
Этот метод применим также и при решении уравнений Вольтерра 2-го рода. В таком случае, ряд Лиувилля - Неймана сходится при любых значениях , а не только при малых.
(3) Линейное уравнение n-го порядка. Общий вид, однородное и неодно-
родное уравнение
Уравнение n-го порядка для одной неизвестной функции z независимого переменного t с постоянными коэффициентами имеет вид:
|
(2.1) |
где a1,,an - постоянные числа (действительные или комплексные). К уравнению (2.1), очевидно, применима теорема существования и единственности, причем интервалом определения решений этого уравнения будет вся действительная ось. (См. соответствующую формулировку в первом параграфе первой главы). Решения уравнения (2.1) будут построены в явном виде и тем самым установлена еще раз теорема существования. Теорема единственности будет использоваться по существу для доказательства того, что найдены все решения данного уравнения.
4)Линейный дифференциальный оператор и его свойства
Пусть 
—
оператор, результат применения которого
к некоторой 
раз
дифференцируемой функции 
дается
формулой
,
(3.4)
Где 
, 
,
…, 
, 
–
некоторые функции.
Этот оператор можно записать символически
.
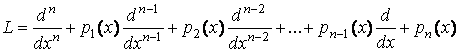(3.5)
Отметим два свойства оператора .
1. Свойство аддитивности. Оператор от суммы функций равен сумме операторов от каждого слагаемого, то есть
.
Действительно,
.
2. Свойство
однородности. Постоянный
множитель можно выносить за знак
оператора, то есть, если 
,
то
.
Имеем:
.
Из этих двух свойств следует, что оператор линейный. Поэтому оператор называется Линейным дифференциальным оператором.
Следовательно,
для любой линейной комбинации функций 
, 
,
…, 
будет
.
Используя оператор и учитывая равенство (3.4), представим неоднородное линейное дифференциальное уравнение (3.2) в виде
.
(3.6)
Однородное линейное дифференциальное уравнение (3.3) примет вид
.
(3.7)
Свойство линейности оператора используется для исследования и отыскания решений линейных дифференциальных уравнений высших порядков.