7. Свойства степенных рядов (без доказательства)

Так как степенные ряды сходятся равномерно на [- r, r], 0 < r < R  (§4, сл. 2), выполняются все

свойства равномерно сходящихся рядов :

1. Сумма степенного ряда – непрерывная функция.

2. Степенной ряд можно почленно интегрировать и дифференцировать. Радиусы сходимости

полученных рядов равны радиусу сходимости исходного.

{Эти свойства непосредственно следуют из равномерной сходимости степенных рядов .

  Последнее утверждение легко проверяется признаками Коши или Даламбера (

8. Ряд Тейлора (вывод разложения)

Если функция   в некотором интервале раскладывается в степенной ряд по степеням  , то это разложение единственно и задается формулой: Примечания: Надстрочный индекс   в последнем слагаемом обозначает производную «энного» порядка. Вместо буквы «а» в литературе часто можно встретить букву  .

Данная формула получила имя некоего англичанина Тейлора (ударение на первый слог).

На практике процентах в 95-ти приходится иметь дело с частным случаем формулы Тейлора, когда  :

Это разложение в ряд обычно называют именем шотландца Маклорена (ударение на второй слог). Разложение Маклорена также называют разложением Тейлора  по степеням  .

Вернемся к таблице разложений элементарных функций и выведем разложение экспоненциальной функции: Как оно получилось? По формуле Маклорена: Рассмотрим функцию  , тогда:

Теперь начинаем находить производные в точке ноль: первую производную, вторую производную, третью производную и т.д.  Это просто, поскольку при дифференцировании экспонента превращается в саму себя:

И так далее….

Совершенно очевидно, что 

Подставляем единицы в формулу Маклорена и получаем наше табличное разложение!

Аналогично можно вывести некоторые другие табличные разложения (но далеко не все выводятся именно так).

9. Разложение e X, cosx, sinx в ряд Тейлора

Функция f(x) = sinx. Получаем f(x) = sinx; f(0) = 0 (0) = 1;/2); f(x) = cosx = sin( x + f (0) = 0;/2); f(x) = -sinx = sin(x + 2f (0)=-1;/2); f(x) = -cosx = sin(x + 3f ………………………………………… f⁽ⁿ⁾n/2); f(x) = sin(x + ⁽ⁿ⁾n/2);(0) = sin( f⁽ⁿ⁺¹⁾/2); f(x) = sin(x + (n + 1)⁽ⁿ⁺¹⁾/2); + (n + 1)) = sin(( Итого: 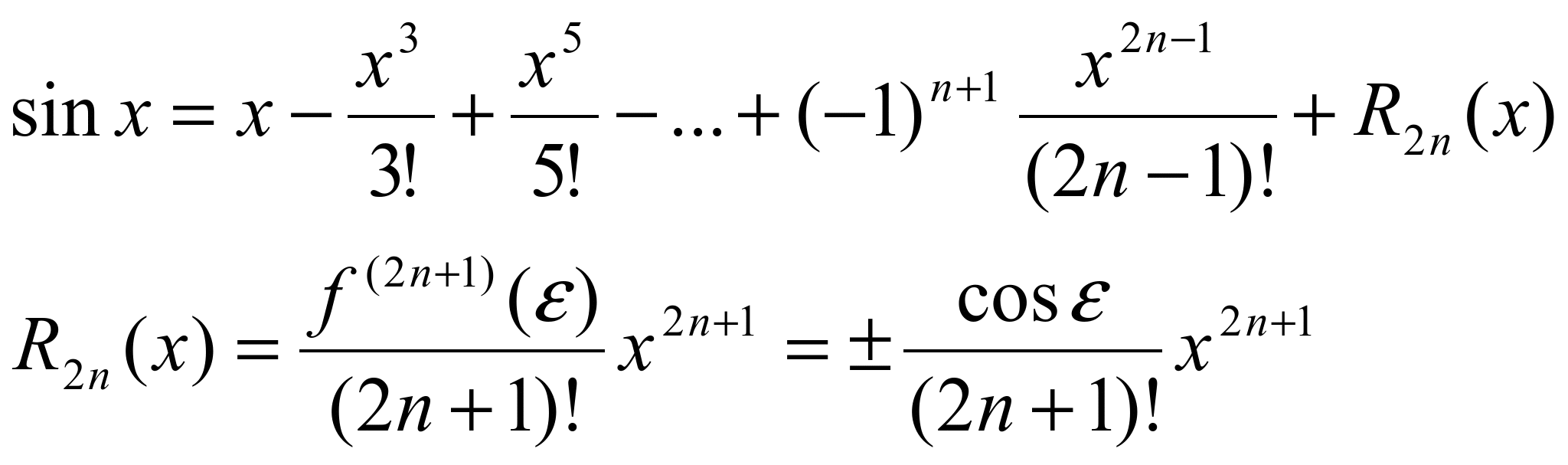 ^ Функция f(x) = cosx. Для функции cosx, применив аналогичные преобразования, получим:

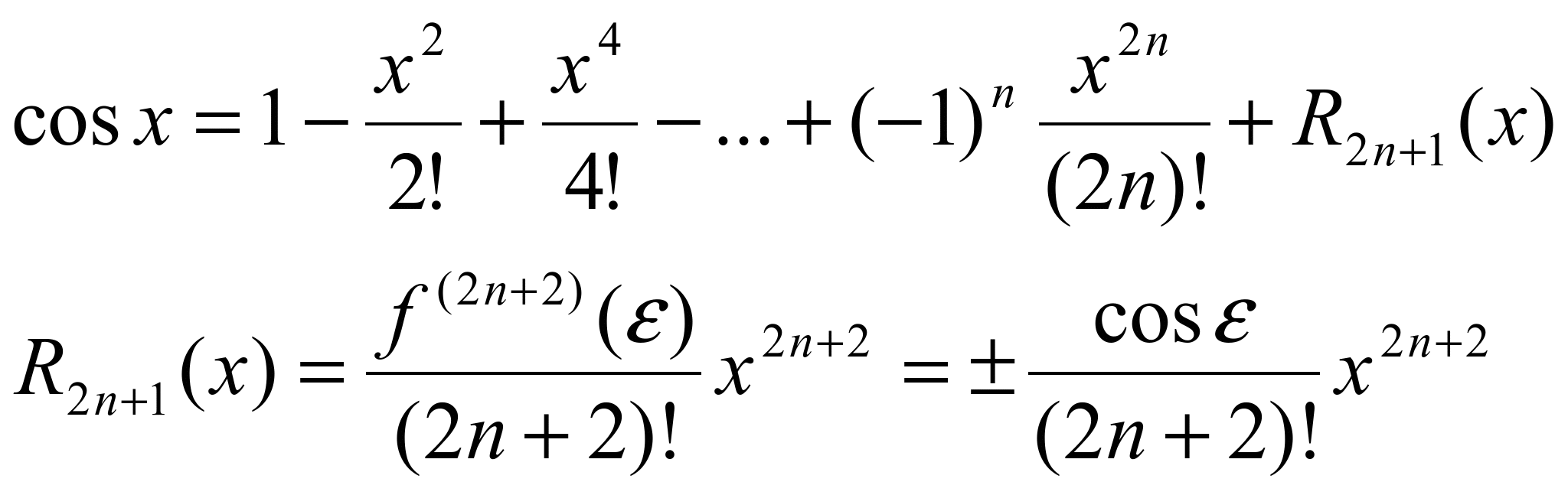
6.Комплексные числа

(1) Алгебраическая форма комплексного числа. Тригонометрическая форма комплексного числа

Ко́мпле́ксные^[1] чи́сла (устар. Мнимые числа^[2]), — расширение поля вещественных чисел, обычно обозначается  . Первоначально обнаружены в результате формального решения некоторых квадратных уравнений, в которых квадрат корня уравнения должен быть отрицательным^[3].

Алгебраическая форма

Запись комплексного числа   в виде  , где   и  , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что  ):