Вопросы к экзамену

1. Неопределенный интеграл

(1) Первообразная. Теорема о множестве первообразных для данной функции.

Первообрáзной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Теорема 1. Если   и   — две  первообразные для функции f (х) в некотором промежутке, то разность между ними в этом промежутке равна постоянному числу.  Из этой теоремы следует, что если известна какая-нибудь первообразная F (х) данной  функции f (х), то все множество первообразных для f (х) исчерпывается функциями F (х) + С.  Выражение F (х) + С, где F (х) —  первообразная функции f (х) и С — произвольная  постоянная, называется неопределенным интегралом от функции f (х) и обозначается символом  , причем f (х) называется подынтегральной функцией ;   — подынтегральным выражением,  х — переменной  интегрирования;  ∫ — знак неопределенного интеграла.

(2) Неопределенный интеграл и его свойства

Неопределенный интеграл — это множество первообразных функции f(x). Обозначается символом  . , где F(x) — некоторая первообразная функции f(x), C — произвольная постоянная.

Свойства неопределенного интеграла

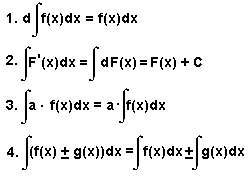
(3) Интегрирование методом замены переменной

Технически метод замены переменной в неопределенном интеграле реализуется двумя способами:

– Подведение функции под знак дифференциала. – Собственно замена переменной.

Одним из наиболее мощных методов интегрирования является замена переменной в интеграле. Поясним суть этого метода. Пусть  , тогда

Но в силу инвариантности формы дифференциала равенство   остается справедливым и в случае, когда   — промежуточный аргумент, т.е.  . Это значит, что формула   верна и при  . Таким образом,

, или  .

Итак, если   является первообразной для   на промежутке  , а   — дифференцируемая на промежутке   функция, значения которой принадлежат  , то   — первообразная для  , и, следовательно,

Эта формула позволяет свести вычисление интеграла   к вычислению интеграла  . При этом мы подставляем вместо  переменную  , а вместо   дифференциал этой переменной, т. е.  . Поэтому полученная формула называется формулой замены переменной под знаком неопределенного интеграла. Она используется на практике как "слева направо", так и "справа налево". Метод замены переменной позволяет сводить многие интегралы к табличным. После вычисления интеграла   надо снова заменить   на  .

(4) Интегрирование по частям

По частям берутся интегралы следующих видов:

1)  ,  ,   – логарифм, логарифм, умноженный на какой-нибудь многочлен.

2)  ,  – экспоненциальная функция, умноженная на какой-нибудь многочлен. Сюда же можно отнести интегралы вроде   – показательная функция, умноженная на многочлен, но на практике процентах так в 97, под интегралом красуется симпатичная буква «е». … что-то лирической получается статья, ах да… весна же пришла.

3)  ,  ,   – тригонометрические функции, умноженные на какой-нибудь многочлен.

4)  ,   – обратные тригонометрические функции («арки»), «арки», умноженные на какой-нибудь многочлен.