
- •3.Деление на двузначное и трехзначное число
- •1) Решение простых задач с недостающими данными.
- •2) Решение пар простых задач, в которых число, полученное в ответе на вопрос первой задачи, является одним из данных во второй задаче.
- •3. Два способа введения составных задач.
- •4.Методика обучения решению задач в два действия, включающих простые задачи на нахождение суммы и на нахождение остатка
- •5.Методика работы над составными задачами
- •3.Пример ознакомления с задачами на пропорциональное деление
- •1.Классификация задач на нахождение четвертого пропорционального
- •1.Присчитывание и отсчитывание
- •2.Прибавление и вычитание по частям
- •4Перестановка слагаемых
- •1. Нумерационные случаи
- •2. Сложение и вычитание целых тысяч
- •3. Сложение и вычитание целых тысяч на основе правил арифметических действий
4Перестановка слагаемых
Правило перестановки слагаемых: От перестановки слагаемых сумма не изменяется.
Свойство перестановки слагаемых (переместительное свойство сложения) используется в 1 классе при знакомстве с вычислительными приемами вида а + 5, а+ 6, а+ 7, а + 8 и а + 9.
№7 Вычислительные приемы для многозначных чисел
Способы устных вычислений
Устные приемы сложения и вычитания многозначных чисел изучаются в 4 классе четырехлетней начальной школы в следующем порядке:
1. Нумерационные случаи
а) Случаи вида:
99 999 + 1 345 ООО - 1 560 999 + 1
560 ООО - 1 399 999 + 1 40 ООО - 1
При выполнении вычислений данного вида ссылаются на принцип построения натурального ряда чисел: добавление к числу единицы дает число, следующее по счету; вычитание единицы дает число, предшествующее по счету.
Например: 399 999 + 1 — добавляя к числу 1, получаем число следующее. Следующее за числом 399 999 число 400 000, значит 399 999 + 1 = 400 000.
б) Случаи вида:
30 000 + 1 000 650 999 - 900 600 000 + 5
60 345 - 5 345 000 - 45 000 800 700 + 1 000
При выполнении вычислений данного вида ребенок должен хорошо знать принцип поразрядного строения чисел в десятичной системе счисления.
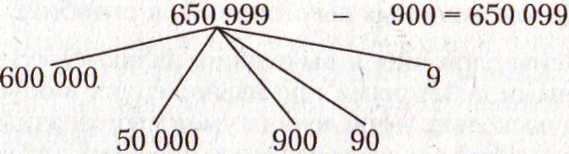
2. Сложение и вычитание целых тысяч
Сложение и вычитание вида 32 000 + 2 000, 690 000 - 50 000 является первым вычислительным приемом, с которого начинается формирование устных вычислений в объеме многозначных чисел.
Для освоения этого приема ребенок должен хорошо представлять разрядный состав многозначного числа. Рассматривая 32 000 как 32 тыс. и 2 000 как 2 тыс., прием 32 000 + 2 000 вычисляется, как 32 тыс. + 2 тыс. Ответ 34 тыс. затем рассматривается, как 34 000 и записывается результат вычислений. Таким образом, действия целыми тысячами рассматриваются как действия разрядными единицами, вычисления в этом случае сводятся к табличным вычислениям в пределах 10, 20 или 100.
3. Сложение и вычитание целых тысяч на основе правил арифметических действий
Учебник математики для 4 класса практически не предлагает вычислений соответствующего вида, однако учителя часто используют их на устном счете.
К этим случаям относятся вычисления вида: 70 200 + 400, 600 100 - 99,3 008 + 351,425 100 - 24 100 и т. п.
При вычислениях используется знание десятичного состава многозначных чисел и понимание того, что во всех случаях действия затрагивают только часть первого числа (первое число может рассматриваться как сумма). Таким образом действия могут выполняться только с частью первого числа.
Например: Вычисляя сумму 70 200 + 400, можно отдельно сложить 400 и 200, а затем их сумму прибавить к числу 70 000. Фактически используется правило прибавления числа к сумме.
При выполнении вычислений в случае 425 100 - 24 100 используется правило вычитания числа из суммы. 425 100 рассматривается, как сумма 400 000 и 25 100. Из одного из слагаемых вычитается 24 100 (25 100 - 24 100 = 1 000), и полученный результат складывается с первым слагаемым: 400 000 + 1 000 = 401 000.
В основе всех этих случаев лежит хорошее знание разрядного состава многозначных чисел и умение выполнять устные вычисления целыми разрядами.
Способы письменных вычислений (в столбик)
Письменные приемы сложения и вычитания являются основными вычислительными действиями при вычислениях в объеме многозначных чисел, поскольку вычисления в уме с многозначными числами представляют собой слишком сложную проблему для всех детей. Использование письменных алгоритмов вычислений в этих условиях является психологически и методически оправданным.
Усвоение детьми нумерации четырехзначных и многозначных чисел позволяет им осуществить перенос умения складывать и вычитать числа «столбиком» из области трехзначных чисел на область многозначных чисел.
При знакомстве с письменными приемами сложения и вычитания в объеме многозначных чисел проводится аналогия с алгоритмом письменного сложения и вычитания в пределах 1000:
1) Письменное сложение и вычитание любых многозначных чисел выполняется так же, как сложение и вычитание трехзначных чисел.
2) При записи столбиком, как и при сложении трехзначных чисел следует записывать разряд под соответствующим разрядом, и складывать сначала единицы, потом десятки, а потом сотни, потом тысячи и т. д. (справа налево).
Считается, что дети хорошо научены выполнять действия сложения и вычитания в столбик, поэтому в учебнике 4 класса не предусмотрено распределение случаев сложения и вычитания по уровням сложности.
Первыми рассматриваются различные случаи с переходами через разряд как при сложении, так и при вычитании: 3 126 + 4 232; 25 346 - 13 407.
Затем рассматриваются случаи вычитания с нулями в уменьшаемом:
600 - 25; 1 ООО - 124; 30 007 - 648.
Эти случаи являются наиболее сложными, поскольку требуют «заема» разрядных единиц не из соседних, а из далеко отстоящих разрядов. Эти случаи полезно сначала сопровождать подробной пояснительной записью на доске, чтобы дети понимали и видели, откуда появляются девятки в «пустых» разрядах.
Например:
В![]() ычитаю
единицы. Из 7 нельзя вычесть 8. Пробую
занять единицу в соседнем разряде.
ычитаю
единицы. Из 7 нельзя вычесть 8. Пробую
занять единицу в соседнем разряде.
В разряде десятков, сотен и тысяч нет разрядных единиц, поэтому «заем» возможно произвести только из разряда десятков тысяч: 30 тыс. - 1 тыс. = 29 тыс. Подписываем 29 над 30.
«Занятую» тысячу представляем в виде суммы 1 тыс. = 1000 = = 990 + 10.
Подписываем над разрядами сотен и десятков девятки, а из 10 единиц вычитаем 8, получаем 2 единицы, Но в разряде единиц было 7 единиц. Добавляем их к полученным 2 единицам и пишем в разряде единиц 9.
Вычитаем: 9 дес. - 4 дес. = 5 дес. Пишем 5 в разряде десятков. 9 сот. - 6 сот. = 3 сот. Пишем 3 в разряде сотен.
От десятков тысяч осталось 29 тыс. Пишем 9 в разряде тысяч, 2 — в разряде десятков тысяч.
При изучении сложения и вычитания многозначных чисел рекомендуется повторять и закреплять названия компонентов и результатов действий; свойства нахождения неизвестных компонентов действий при проверке результатов вычислений; рассматривать закономерности изменения суммы и разности при изменении одного из компонентов действий.
Чтобы стимулировать ребенка к использованию умения самостоятельно вычислять в столбик, следует предлагать задания, не позволяющие механического использования калькулятора для вычисления результата. Это различные задания на нахождение ошибки в записях или цифрах вычислений, на прикидку округленных результатов вычислений, на восстановление пропущенных цифр в компонентах действий, на выбор верных ответов из предложенных и т. п. Учителю следует помнить, что механический характер вычислительных действий при вычислениях с многозначными числами быстро приводит к утомлению детей, что провоцирует появление ошибок. Поэтому не стоит задавать подряд больше трех примеров на вычисления с многозначными числами.
№ 26 Методика изучения дробей
В начальных классах, с целью подготовки к изучению дробей в 5 классе, по традиционной программе во 2 классе изучаются доли величины, их обозначение и сравнение, нахождение доли числа и числа по его доле; в 3 классе - образование дробей, их чтение и запись, сравнение дробей (простейшие случаи), нахождение части числа. Все эти вопросы раскрываются на наглядной основе.
К концу обучения в начальной школе учащиеся должны уметь: 1. Показывать и называть доли прямоугольника, круга и отрезка. 2. Читать и записывать доли в виде дроби со знаменателем, не превышающим число 10. 3. Решать задачи на нахождение доли числа и числа по его доле. 4. Показывать и называть часть прямоугольника, круга, отрезка. 5. Читать и записывать обыкновенные дроби со знаменателем, не превышающим числа 10; пользуясь записью дроби, сказать, на сколько равных частей, долей разделена величина и сколько таких частей взято. 6. Уметь сравнивать дроби, опираясь во всех случаях на рисунок. 7. Решать задачи на нахождение дроби числа.
Ознакомление с долями
Основная задача при ознакомлении с долями - научить детей практически образовать доли по математической записи и обратно: записывать доли, исходя из практических действий. Например, чтобы получить одну третью долю круга, надо круг разделить на три равные части и взять одну такую часть; если круг разделили на шесть равных частей и взяли одну часть - это значит одна шестая доля круга.
При ознакомлении с долями у каждого ученика должны быть наглядные пособия, с которыми он работает, дублируя действия учителя. Предварительно создавая проблемную ситуацию, учитель мотивирует необходимость изучения новых чисел. После этого объявления темы, предлагает учащимся взять свои квадраты (заранее приготовлены) и просит их перегибанием разделить на две равные части (показывает как надо делать). Разрезав по линии сгиба, учитель наложением показывает учащимся, что две половинки равные и одну половинку называет "это одна вторая доля квадрата". После этого просит их показать одну вторую долю своего квадрата. Далее выясняют, что целый квадрат состоит из двух вторых частей.
Далее учащиеся аналогичным образом получают одну четвертую долю квадрата. После этого показываем запись долей: 1/2 и объясняем: число 2 показывает, что квадрат разделили на две равные части, а число 1 показывает, что взяли одну такую часть и т.д.
Закрепляя понятие доли, учащимся предлагаются вопросы:
1) Объясните, как получить 1/2 долю круга?
2) Что означает выражение " 1/5 отрезка"?
3) Круг разделили на 7 равных частей. Как назовете одну такую часть?
4) Отрезок разделили на 4 разные части. Можно ли одну часть назвать "одной четвертой долей отрезка"?
5) Назовите, какая доля прямоугольника закрашена и запишите эту долю (рис.115). Что обозначают в этой записи числа, записанные выше черты и ниже черты?
Ознакомление с дробями
Образование дробей, как и образование долей рассматривается с помощью наглядных пособий.
Р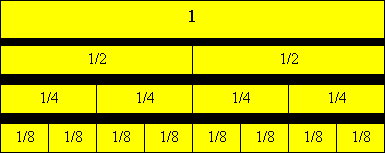 азделите
круг на 4 равные части. Как назвать
каждую такую часть? (Одна четвертая
круга.) Покажите две четвертые доли. Вы
получили дробь - две четвертых. Это
записывают так 2/4. Сколькими частями
вы покажете дробь 3/4? (Три четвертые
доли.) Мы записали дроби 2/4, 3/4. Что
показывает число 4? (Число 4 показывает,
на сколько равных частей разделили
круг.) А что показывают числа 2 и 3?
(Сколько таких равных частей взяли.)
Дроби 2/4 и 3/4 читают так: две четвертых,
три четвертых. А теперь прочитайте
упражнение учебника и объясните, как
получены указанные дроби.
азделите
круг на 4 равные части. Как назвать
каждую такую часть? (Одна четвертая
круга.) Покажите две четвертые доли. Вы
получили дробь - две четвертых. Это
записывают так 2/4. Сколькими частями
вы покажете дробь 3/4? (Три четвертые
доли.) Мы записали дроби 2/4, 3/4. Что
показывает число 4? (Число 4 показывает,
на сколько равных частей разделили
круг.) А что показывают числа 2 и 3?
(Сколько таких равных частей взяли.)
Дроби 2/4 и 3/4 читают так: две четвертых,
три четвертых. А теперь прочитайте
упражнение учебника и объясните, как
получены указанные дроби.
После ознакомления с дробями учащиеся выполняют упражнения:
1) на объяснение образования дробей по готовому рисунку;
2) на запись дробей по готовому рисунку;
3) изображение дробей с помощью отрезка (например, покажи 3/5 отрезка);
4) на сравнение дробей в основном по изображению равных прямоугольников.
Учащимся предлагается начертить 4 одинаковых прямоугольника: В первом целом прямоугольнике запишем число 1. Второй прямоугольник разделите на 2 равные части и запишите полученные доли. Сколько вторых долей в целом прямоугольнике? Третий прямоугольник разделите на 4 равные части и запишите полученные доли. Сколько четвертых долей в целом прямоугольнике? Сколько четвертых долей в половине? Что больше: одна вторая или одна четвертая? Запишем так: (1/2 > 1/4). Какие числа знаки поставим, чтобы следующие равенства и неравенства были верными: 1/2 = □ /4, 3/4 * 1/2, 2/4 * 3/4? Следующий прямоугольник делится на 8 равных частей и учащиеся отвечают на аналогичные вопросы.
Сравнение дробей можно иллюстрировать отрезками, рассуждая при этом так: "на отрезке покажу 2/5 и 3/4: для этого его разделю на 5 равных частей и возьму 2 части; такой же отрезок разделю на 4 равные части и возьму 3 части. Вижу, что второй от резок, отмеченный дугой, длиннее и поэтому 3/4 > 2/5.
№ 24 Задачи и содержание работы по изучению элементов геометрии
Тема «Элементы геометрии» занимает значительное место в программе по математике и изучается в течение всего периода начального обучения. Как правило, отдельные вопросы, относящиеся к теме, не выделяются в отдельные блоки, а переплетаются с изучением основного – арифметического – материала. Отдельно представлено измерение площади, углов, объема пространственных фигур и геометрических моделей числового ряда (числовой (координатный) луч).
Сравнительно большой объем в курсе начальной школы отводится на изучение геометрического материала. Это объясняется двумя основными причинами:
1) работа с геометрическими объектами позволяет активно использовать наглядно-действенный, наглядно-образный и наглядно-логический уровни мышления, которые наиболее близки младшим школьникам и опираясь на которые дети выходят на высшую ступень в своем развитии – словесно-логический уровень;
2) увеличение объема изучения геометрического материала в начальных классах, особенно связанного с объемными фигурами, способствует более эффективной подготовке учеников к изучению систематического курса геометрии, что позволяет снизить у школьников основного и старшего звена школы существенные трудности, возникающие при изучении геометрии.
Перечислим основные задачи изучения темы «Элементы геометрии»:
– уточнение и обобщение геометрических представлений, полученных в дошкольном возрасте;
– обогащение геометрических представлений школьников, формирование некоторых основных геометрических понятий (фигура, плоскостные и пространственные фигуры, основные виды плоскостных и пространственных фигур, их иерархическая связь между собой и т.д.);
– развитие плоскостного и пространственного воображения школьников;
– подготовка к изучению систематического курса геометрии в основном звене школы.
Решение первой задачи, особенно на первом этапе обучения, предполагает уточнение терминологии, которой пользуются дети, а также осознание признаков, позволяющих отнести геометрические фигуры к соответствующей категории.
Еще до школы практически все дети знакомятся с такими геометрическими фигурами, как круг, квадрат, треугольник, прямоугольник, овал. С ними же они сталкиваются и на уроках математики. Учителю необходимо использовать каждую ситуацию, когда дети в своей речи используют слова «кружок», «квадратик» и т.п., для замещения этих названий математическими «круг», «квадрат», «треугольник» и т.д. Так же важно, чтобы учитель следил и за собственной речью – не говорил: «Нарисуйте три кружка...» Дети постепенно овладеют правильной терминологией.
Сравнивая знакомые фигуры между собой, дети начинают осознавать, в чем заключается сходство и различие фигур. Так, они замечают, что в треугольнике меньше сторон и углов, чем в квадрате. Уже на этом этапе дети устанавливают связь между названием «треугольник» и числом углов в этой фигуре.
После установления связи между названием и числом углов треугольника необходимо продолжить эту линию и предложить детям дать другое название квадрату. Однако переключение со знакомого, привычного названия фигуры на новое может оказаться для учеников слишком трудным. В этом случае выйти на термин «четырехугольник» можно при рассмотрении произвольного четырехугольника, а затем подвести под этот термин и такие знакомые фигуры, как квадрат и прямоугольник.
Приведенная выше работа подготавливает почву для решения одного из важных аспектов решения второй задачи – формирования общего способа классификации многоугольников по числу углов. Предлагая регулярно для рассмотрения многоугольники с различным количеством углов, помогая детям найти их названия, учитель продвигает детей в осознании этого способа классификации.
С первых уроков начинается знакомство с простейшими геометрическими фигурами – точкой и линией – на уровне наглядного восприятия моделей этих фигур как в виде изображения их на чертеже, так и в качестве элементов реальных объектов, окружающих детей.
На протяжении всего обучения в начальной школе дети занимаются сравнением и выявлением свойств различных плоскостных и объемных геометрических фигур, связей между ними, их классификацией. Такой подход к изучению материала способствует сознательному овладению знаниями и продвижению детей в развитии.
Чтобы ученики представили себе такое понятие, как бесконечность прямой, мы предлагаем сначала использовать такую практическую работу: как можно более длинные, толстые и яркие нитки наматывают примерно поровну на 2 катушки. Таких пар катушек нужно заготовить вдвое меньше, чем учеников в классе. Дети выходят в коридор или на пришкольный участок, делятся на пары. Учитель дает каждой паре один из заготовленных комплектов, каждый ученик берет одну катушку, и пары становятся лицом друг к другу, туго натягивая разделяющую их часть нитки. По команде учителя пары начинают медленно расходиться в противоположные стороны, разматывая натянутую нитку.
Если у кого-то из детей кончается нитка, но есть место для продолжения движения, можно привязать дополнительный кусок нитки, но можно этого и не делать.
После завершения практической работы необходимо обсудить с детьми причины, по которым им пришлось остановиться, и что можно было сделать, чтобы продолжить движение. Таких причин две:
– закончилась нитка, и в этом случае поможет увеличение длины нитки;
– нет возможности двигаться дальше, так как на пути возникло препятствие, и в этом случае нужно представить, что препятствие убрано с пути каким-либо способом.
В качестве следующего шага можно использовать такой прием: на доске чертится часть прямой. Учитель спрашивает, можно ли эту прямую продолжить, сделать длиннее. Возможно, дети сразу догадаются, что можно. Если такой ответ получен, нужно предложить рассказать, как это можно сделать (приложить линейку к части начерченной линии и начертить дальше). Учитель выполняет эту операцию и спрашивает, можно ли еще продолжить эту прямую. Постепенно прямая продолжается до краев доски. А дальше можно? Очевидно, дети скажут, что дальше чертить нельзя. На этом этапе устанавливается, что причина не в том, что прямая не может продолжаться, а в том, что кончилась доска. Дальше учитель предлагает детям представить, какой длины можно было бы начертить прямую, если ее чертить не на доске, а на стене, на полу класса, в коридоре, на земле во дворе и т.д. Так постепенно у учащихся формируется понимание возможности неограниченного продолжения прямой.
После знакомства с прямой рассматривают фигуры, которые являются ее частями: луч и отрезок. Прямую, луч и отрезок сравнивают между собой, устанавливают отличие луча от отрезка и от прямой. При знакомстве с отрезком основное внимание уделяется его ограниченности с двух сторон, а луча – с одной стороны.
Можно использовать такой вариант знакомства с отрезком: на доске изображаются две точки. Затем формулируется задание: соединить точки линией. Учитель не должен торопиться с разъяснениями – нужно предоставить ученикам время для самостоятельного выполнения задания. Только после этого несколько учеников показывают на доске свои решения, используя одну и ту же пару точек. На доске получается чертеж, на котором две точки соединены несколькими разными линиями. Очень важно так подобрать решения детей, чтобы были выявлены все допущенные ошибки (например, вместо того чтобы соединить точки линией, ученик проводит линию через две точки, то есть концы линии не находятся в данных точках) и были представлены все принципиально разные варианты решений. Если среди них будет отрезок, учителю останется только сконцентрировать внимание учеников на этом решении, выделив его среди других, что нетрудно сделать, так как все остальные решения, очевидно, будут кривыми линиями. Кроме того, дети легко заметят, что эта линия является самой короткой. Если среди предложенных детьми решений отрезка не окажется, учитель предлагает выполнить задание.
Дальнейшее продвижение в знакомстве с геометрическим материалом тесно связано с взаимным расположением различных линий, особенно прямых, лучей и отрезков, что приводит к знакомству с различными новыми геометрическими фигурами (углами, ломаными линиями, многоугольниками и т.д.).
Весь остальной геометрический материал изучается аналогично, начиная с основополагающего понятия и постепенно расширяя и углубляя тему. Такое построение материала является второй особенностью изучения элементов геометрии, хотя относится не только к нему.
№ 20 СМЫСЛ ДЕЙСТВИЯ УМНОЖЕНИЯ
Действие умножения рассматривается как суммирование одинаковых слагаемых.
С теоретико-множественной точки зрения умножению соответствуют такие предметные действия с совокупностями (множествами, группами предметов) как объединение равных (равночисленных) совокупностей. Поэтому, прежде, чем знакомиться с символикой записи действий и вычислениями результатов действий, ребенок должен научиться моделировать на предметных совокупностях все эти ситуации, понимать (т. е. правильно представлять) их со слов учителя, уметь показывать руками как процесс, так и результат предметного действия, а затем характеризовать их словесно.
Виды заданий, предлагаемые до знакомства с символикой действия умножения (в 1 и 2 классе):
1. Посчитай двойками (тройками, пятерками).
2. Нарисуй рисунок: «На трех тарелках по 2 апельсина». Сосчитай, сколько всего апельсинов.
3. Найди лишнюю запись: 2 + 2
2 + 2 + 2
2 + 2 + 2 + 2
2 + 3 + 2 + 2 + 2
Найди значение каждого выражения наиболее удобным способом.
4![]() .
Сделай запись выражения по рисунку:
.
Сделай запись выражения по рисунку:
Виды заданий, используемые для усвоения смысла умножения при знакомстве с этим действием:
а) На соотнесение рисунка и математической записи:.:Рассмотри рисунок и объясни записи:
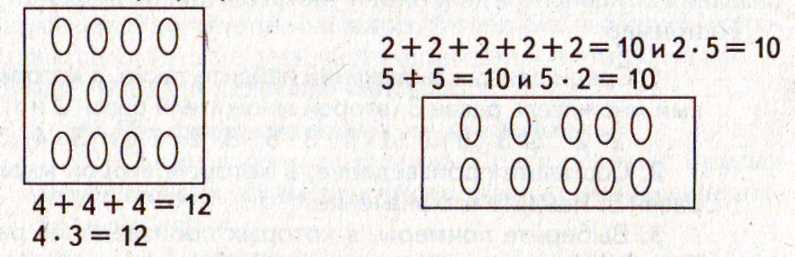 б)
На нахождение суммы одинаковых
слагаемых:Рассмотри рисунки и закончи
записи:
б)
На нахождение суммы одинаковых
слагаемых:Рассмотри рисунки и закончи
записи:
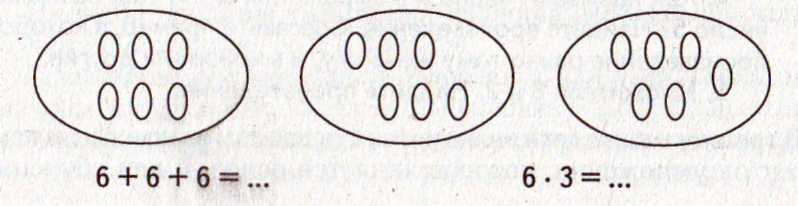
в) На замену сложения умножением: Замени, где возможно сложение умножением и вычисли результаты: 5+5+5+5 1+1+1+1+1 5+6+3
42 + 42 0 + 0 + 0 + 0 + 0 4 + 6 + 8
г) На понимание смысла определения действия умножения:
Рассмотри записи и объясни, какое число берется слагаемым и сколько раз берется слагаемым это число: 6 • 4 = 24 9 • 3 = ...
6 + 6 + 6 + 6 = 24 9 + 9 + 9 = ...
Выражение вида 3 • 5 называют произведением. Числа 3 и 5 в этой записи называют множителями.
Запись вида 3 • 5 = 15 называют равенством. Число 15 называют значением выражения. Поскольку число 15 в данном случае получено в результате умножения, его также часто называют произведением.
Поскольку названия компонентов действия умножения вводятся по соглашению (детям сообщаются эти названия и их необходимо запомнить), педагог активно использует задания на распознавание компонентов действий и употребления их названий в речи.
Например:
1. Среди данных выражений найдите такие, в которых первый множитель равен 3 (второй множитель равен 2 и т. д.):
2• 2 7• 3 6• 2 1• 6 3• 5 3• 2 7• 3 3• 4 3• 1
2. Составьте произведение, в котором второй множитель равен 5. Найдите его значение.
3. Выберите примеры, в которых произведение равно 6. Подчеркните их красным цветом. Выберите примеры, в которых произведение равно 12. Подчеркните их синим цветом.
7 • 3 6 • 1 2 • 2 2 • 3 6 • 2 3 • 2 2 • 6
4. Как называют число 4 в выражении 5 • 4? Как называют число 5? Найдите произведение. Составьте пример, в котором произведение равно тому же числу, а множители другие.
5. Множители 8 и 2. Найдите произведение.
В 3-м классе дети знакомятся с правилом взаимосвязи компонентов умножения, которое является основой для обучения нахождению неизвестных компонентов умножения при решении уравнений:
Если произведение разделить на один множитель, то получится другой множитель.
Например: Решите уравнение 6 • х = 24. (В уравнении неизвестен множитель. Чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель. х= 24:6, х = 4.)
От перестановки множителей произведение не меняется.
Способ знакомства детей с этим правилом (законом) обусловлен ранее введенным смыслом действия умножения. Используя предметные модели множеств, дети сосчитывают результаты группировки их элементов разными способами, убеждаясь, что результаты не меняются от изменения способов группировки.
Счет элементов рисунка (множества) парами по горизонтали совпадает со счетом элементов тройками по вертикали. Рассмотрение нескольких вариантов подобных случаев дает учителю основание произвести индуктивное обобщение (т. е. обобщение нескольких частных случаев в обобщенном правиле) о том, что перестановка множителей не меняет значение произведения.
Смысл действия деления
Действие деления рассматривается в начальной школе как действие, обратное умножению.
С теоретико-множественной точки зрения смыслу деления соответствует операция разбиения множества на равночисленные подмножества. Таким образом, процесс нахождения результатов действия деления связан с предметными действиями двух видов:
а) разбиение множества на равные части (например, 8 кружков разложили в 4 коробки поровну — раскладывают 8 кружков по одному в 4 коробки, а затем считают, сколько кружков получилось в каждой коробке);
б) разбиение множества на части по сколько-то в каждой части (например, 8 кружков разложили в коробки по 4 штуки — раскладывают 8 кружков по 4 штуки в коробки, а затем считают, сколько получилось коробок; деление по этому принципу в методике называют «деление по содержанию»).
Используя подобные предметные действия и рисунки, дети находят результаты деления.
Выражение вида 12:6 называют частным. Число 12 в этой записи называют делимым, а число 6 — делителем. Запись вида 12 : 6 = 2 называют равенством. Число 2 называют значением выражения. Поскольку число 2 в данном случае получено в результате деления, его также часто называют частным.
Задания, требующие распознавания компонентов действий и употребления их названий в речи.
1. Среди данных выражений найдите такие, в которых делитель равен 3:
2:2 6:3 6:2 10:5 3:1 3-2 15:3 3-4
2. Составьте частное, в котором делимое равно 15. Найдите его значение.
3. Выберите примеры, в которых частное равно 6. Подчеркните их красным цветом. Выберите примеры, в которых частное равно 2. Подчеркните их синим цветом.
4. Как называют число 4 в выражении 20: 4? Как называют число 20? Найдите частное. Составьте пример, в котором частное равно тому же числу, а делимое и делитель — другие.
5. Делимое 8, делитель 2 . Найдите частное.
В 3 классе дети знакомятся с правилом взаимосвязи компонентов деления, которое является основой для обучения нахождению неизвестных компонентов деления при решении уравнений:
Если делитель умножить на частное, то получится делимое.
Если делимое разделить на частное, то получится делитель.
Например:Решите уравнение 16 : х= 2. (В уравнении неизвестен делитель. Чтобы найти неизвестный делитель, нужно делимое разделить на частное. х= 1.6 : 2, х= 8.)
№ 3 Этапы решения задачи
Процесс решения каждой арифметической задачи осуществляется поэтапно, независимо от способа решения.
Рассмотрим возможный план работы учащихся над задачей:
1.Анализ текста задачи;
2. Схематическая запись условия;
3. Поиск решения; составление плана решения;
4. Осуществления плана решения задачи;
5. Проверка полученного ответа.
Этот план может существенно меняться, если задача решается устно или составлена по иллюстрации.
1.Анализ текста задачи. Основное назначение этапа – осмыслить ситуацию, отраженную в задаче; выделить условие и требования, назвать данные и искомые, выделить условия и требования, назвать данные и искомые, выделить величины и зависимости между ними (явные и неявные).
На этом этапе решения задачи используют следующие приемы.
1. О чем эта задача?
2. Что требуется найти в задаче?
3. Что означают слова 'за все это время'?
4. Что в задаче известно о движении каждого из участников его?
5. Что дальше известно?
6. Что является искомым: число, значение величины, вид некоторого отношения?
Большую помощь в осмыслении содержания задачи и создания основы для поиска решения задачи оказывает переформулировка текста задачи – замена данного в нем описания ситуации другим, сохраняющим все отношения, связи и количественные характеристики, но и более явно их выражающим.
2. Схематическая запись условия
Составление по условию задачи чертежа, схемы, рисунка и т. д., т.е. интерпретация условия задачи – не самоцель. Она выполняется (учителем, или учащимися под руководством учителя, или самими учащимися – в зависимости от их подготовки, от сложности задачи) только тогда, когда ученики не могут решить данную задачу. Видов интерпретации условия: Краткая запись условия задачи, чертеж по условию задачи .
3. Поиск решения; составление плана решения.
Цель данного этапа – завершить установление связей между данными и искомыми величинами и указать последовательность использования этих связей.
Решение задач – сложная интеллектуальная деятельность. Описать ее содержание в полном объеме невозможно, даже если иметь в виду деятельность, осуществляемую младшим школьником.
На этом этапе ученики должны выделить величины, входящие в задачу, данные и искомые числа, установить связи между данными и искомым и на этой основе выбрать соответствующие арифметические действия.
Проведя анализ задачи, не всегда просто найти путь ее решения. Поиск пути решения задачи является достаточно трудным процессом, для которого нет точного предписания. Укажем некоторые приемы, которые помогают осуществлять этот этап.
Одним из приемов поиска пути решения задачи является разбор задачи по тексту или по ее вспомогательной модели. Поиск пути решения задачи можно осуществлять от вопроса задачи к данным (аналитический путь) или от данных к вопросу (синтетический путь).
При разборе задачи нового вида учитель должен в каждом отдельном случае поставить детям вопросы так, чтобы навести их на правильный или осознанный выбор арифметических действий.
Очень важно чтобы вопросы не были подсказывающими, а вели бы к самостоятельному нахождению пути решения задачи.
Разбор задачи заканчивается составлением плана решения.
План решения – это объяснение того, что узнаём, выполнив то или иное действие, и указания по порядку арифметических действий.
Часто при введении задач нового вида ученики затрудняются самостоятельно составить план решения, тогда им помогает учитель.
4. Осуществления плана решения задачи.
Назначением этапа – найти ответ на требование задачи. Немало важную роль при решении задач играет запись найденного решения.
Решение задачи может быть выполнено устно или письменно. При устном решении соответствующие арифметические действия и пояснения выполняются устно. При этом надо учить детей правильно и кратко давать пояснения к выполняемым действиям.
При письменном решении записываются действия, а пояснения к ним учащиеся либо записывают, либо проговаривают устно.
В начальных классах могут быть использованы такие основные формы записи решения:
1)составление по задаче выражения и нахождение его значения;
2)составление по задаче уравнения и его решение;
3)запись решения в виде отдельных действий.
В большинстве случаев надо отдавать предпочтение первым двум формам записи решения. При такой записи учащиеся сосредотачивают главное внимание на логической последовательности действий, а не на результатах вычисления, при этом они оперируют выражениями, что способствует формированию понятия выражения, кроме того, само по себе составление по условиям задач уравнения и выражения ценно с точки зрения приобщения детей к алгебраическому способу решения задач.
Запись решения в виде отдельных действий используется, как правило, тогда, когда уравнение или выражение очень сложно и громоздко, а иногда их составить и невозможно, и в тех случаях, когда задача включает большие числа.
5. Проверка полученного ответа.
Проверить решение задачи – значит установить, что оно правильно или ошибочно.
В начальных классах используются следующие четыре способа проверки: составление и решение обратной задачи; установление соответствия между числами, полученными в результате решения задачи, и данными числами; решение задачи другим способом; прикидка ответа.
Составление и решение обратной задачи.В этом случае детям предлагается составить и решить задачу, обратную данной. Если при решении обратной задачи в результате получится число, которое было известно в данной задаче, то можно считать, что данная задача решена правильно.
Установление соответствия между числами, полученными в результате решения задачи, и данными числами. При проверке решения задачи данным способом выполняют арифметические действия над числами, которые получатся в ответе на вопрос задачи; если при этом получатся числа, данные в условии задачи, то можно считать, что задача решена правильно.
Решение задачи другим способом. Если задачу можно решить различными способами, то получение одинаковых результатов подтверждает, что задача решена правильно.
Прикидка ответа. Применение этого способа состоит в том, что до решения задачи, устанавливается область значений искомого числа, т.е. устанавливается больше или меньше какого-то из данных чисел должно быть искомое. После решения задачи определяется, соответствует ли полученный результат установленной области значений, если он не соответствует, значит, задача решена не правильно.
Следует подчеркнуть, что в реальном процессе решения задачи, отмеченные этапы не имеют четких границ и не всегда выполняются одинаково полно. Так, иногда уже при восприятии задачи решающий может обнаружить, что данная задача - известного ему вида, и он знает, как ее решать. В том случае поиск решения не вычленяется в отдельный этап и обоснование каждого шага при выполнении первых трех этапов делает необязательной проверку после выполнения решения. Однако полное, логически завершенное решение обязательно содержит все этапы. А знание возможных приемов выполнения каждого из этапов делает процесс решения любой задачи осознанным и целенаправленным, а значит, и более успешным.
В процессе решения текстовых арифметических задач различных типов у учащихся начальной школы должны вырабатываться общие приемы решения задачи. Этой целью учитель организует работу над задачей, как правило, по одному и тому же плану. Накапливая опыт такой работы, ученики все с большей степенью самостоятельности применяют соответствующие умения.
№ 21. Задачи на нахождение неизвестных по двум разностям
Включают две переменные и одну или несколько постоянных величин, причем даны два значения одной переменной и разность соответствующих значений другой переменной, а сами значения этой переменной являются искомыми.
По отношению к каждой тройке величин, находящихся в пропорциональной зависимости, можно выделить шесть видов задач на нахождение неизвестных по двум разностям. Однако в начальных классах ограничиваются рассмотрением двух следующих видов задач.
Сначала рассматриваются задачи I вида, а затем II. Эти задачи решаются только способом нахождения значения постоянной величины.
До ознакомления с решением задач на нахождение неизвестных по двум разностям важно предусмотреть специальные подготовительные упражнения, с помощью которых раскрывается основная проблема задачи.
В качестве п о д г о т о в и т е л ь н ы х у п р а ж н е н и й к введению задач этого типа полезно предлагать задачи-вопросы и простые задачи повышенной трудности, которые помогут детям уяснить соответствие между двумя разностями, например:
1) Сестра купила 5 одинаковых тетрадей, а брат 8 таких же тетрадей. Кто из них больше уплатил денег? Почему? За сколько тетрадей брат уплатил столько же денег, сколько уплатила сестра?
2) Брат и сестра купили тетради по одинаковой цене. Брат купил на 3 тетради больше, чем сестра, и уплатил на 9 руб. больше, чем сестра. Сколько стоила одна тетрадь?
Выполняя предметную иллюстрацию, надо показать детям, что брат купил столько же тетрадей, сколько сестра, и еще 9 руб. Отсюда можно заключить, что три тетради стоят 9 руб., значит, можно узнать, сколько стоит одна тетрадь.
Такие упражнения надо включать с различными группами пропорциональных величин.
После подготовительных упражнений можно перейти к ознакомлению с решением задач на нахождение неизвестных по двум разностям. Здесь, как и при ознакомлении с задачами на пропорциональное деление, можно использовать различные пути: можно сначала составить задачу на нахождение неизвестных по двум разностям, преобразовав знакомую задачу на нахождение четвертого пропорционального, а можно сразу предложить готовую задачу. В том и в другом случае надо записать кратко в таблице или выполнить рисунок и после того коллективного составления плана записать решение (лучше отдельными действиями с пояснениями).
На этапе закрепления умения решать задачи на нахождение неизвестных по двум разностям можно использовать упражнения аналогичные тем, которые предлагались при решении задач на пропорциональное деление. После введения задач на нахождение неизвестных по двум разностям второго вида. По аналогичной методике следует провести работу по сравнению задач этих двух видов и сравнению их решении. Полезны также упражнения по сравнению задач на пропорциональное деление и задач соответствующего вида на нахождение неизвестных по двум разностям.
Итак, задачи на нахождение неизвестного по двум разностям – задачи, которые включают две переменные величины и одну постоянную, причем даны два значения одной переменной и разность соответствующих значений другой переменной, а сами значения этой переменной являются искомыми. Эти задачи решаются только способом нахождения значения постоянной величины.
№ 19. Тысяча
Нумерация в пределах 1000 и арифметические действия выделяются в особый концентр по следующим причинам:
- здесь заканчивается изучение нумерации чисел первого класса, класса единиц (сотни, десятки, единицы), что является основой для изучения нумерации многозначных чисел;
- закрепляются знания устных и письменных приемов вычислений;
- вводятся устные приемы умножения и деления;
- далее продолжается решение составных задач с новыми величинами, изучение геометрического и алгебраического материала.
В результате изучения нумерации учащиеся должны:
- уметь читать и записывать трехзначные числа;
- понимать образование чисел из сотен, десятков, единиц;
- усвоить названия разрядных единиц, их соотношение и уметь представлять число как сумму разрядных слагаемых;
- уметь применять знание нумерации при устных вычислениях.
Методика изучения нумерации в пределах 1000 аналогична методике изучения нумерации в пределах 100. Разница только в том, что здесь добавляется еще один разряд - разряд сотен.
Перед изучением нумерации в пределах 1000 учитель посвящает один урок повторению всех видов упражнений по нумерации в пределах 100, работает по общей схеме разбора числа, повторяет все термины.
С помощью наглядных пособий учащиеся отсчитывают 10 десятков и заменяют их одной сотней, затем отсчитывают 10 сотен и заменяют их одной тысячей.
При хорошо развитом восприятии и воображении достаточным оказывается и рисунок учебника. При изучении письменной нумерации в абаке появляется еще один кармашек с надписью "Сотни". Продолжается работа по нумерационной таблице. Основные виды упражнений такие, какие указаны в общей схеме разбора числа.
Для закрепления нумерации в пределах 1000 вводятся величины: километр, килограмм, грамм и соотношения между ними.
Многозначные числа
Нумерация многозначных чисел и действия над ними выделяются в особый концентр по следующим причинам:
- многозначные числа образуются, называются, записываются с опорой и на понятие разряда, и на понятие класса;
- арифметические действия, в основном, выполняются с использованием письменных вычислений.
В результате изучения нумерации многозначных чисел учащиеся должны:
- усвоить названия и последовательность чисел натурального ряда в пределах класса миллионов, понять, как они образуются, знать их десятичный состав;
- знать названия классов (класс единиц, класс тысяч, класс миллионов) и разрядов внутри каждого класса (единицы, десятки, сотни, единицы тысяч, десятки тысяч и т.д.);
- научиться читать и записывать любое число в пределах класса миллионов, представлять любое число в виде суммы его разрядных слагаемых;
- уметь переносить все приемы работы над числами, изученными в предыдущих концентрах, в данный концентр.
Изучение нумерации многозначных чисел начинают с повторения нумерации чисел в пределах 1000. Повторяются все виды упражнений по общей схеме разбора числа, повторяется работа с нумерационной таблицей, все термины, относящиеся к нумерации. Наиболее удобным наглядным пособием для изучения многозначных чисел являются русские счеты.
После ознакомления с числами 10000, 100000, учащиеся знакомятся классами: 1 класс - класс единиц, 2 класс - класс тысяч (читают по учебнику). Затем сравнивают 1 и 2 классы и устанавливают их сходство и различие: в каждом классе по три разряда, единицы каждого разряда в 10 раз больше предыдущей, но в 1 классе считают и группируют единицы, а в 2 классе - тысячи.
Далее изучаются числа 2 класса - числа вида 75000, 600000, 392000. Работа, в основном, ведется по нумерационной таблице. Выставляя соответствующие цифры учитель обращает внимание на особенности записи чисел 2 класса: три нуля в конце обозначают отсутствие единиц 1, 2, 3 разрядов, т.е. отсутствие единиц 1 класса, но не отсутствие самих разрядов или класса. Рассматривая десятичный состав чисел 2 класса, учащиеся говорят: 392000 - это 3 сотни тысяч, 9 десятков тысяч и 2 единиц тысяч. Повторяют также другие упражнения по общей схеме разбора числа.
На следующем этапе изучаются числа, состоящие из единиц первого и второго класса. Первые упражнения проводятся по нумерационной таблице, куда выставляются карточки с цифрами. Учащимся надо показать порядок чтения таких чисел, показывая это стрелкой (по табл.23):
В дальнейшем при разборе числа ограничиваются названием разрядов: 923427 - это 923427 единиц; 92342 десятка; 9234 сотни; 923 тысячи; 92 десятки тысяч; 9 сотен тысяч.
Для закрепления нумерации многозначных чисел рассматриваются, в частности, такие упражнения:
а) устное сложение и вычитание вида 17350-350, 40000+60 и т.п.;
б) во сколько раз увеличится число, когда в его записи справа приписывается один нуль? два нуля? три нуля? (аналогично: если отбросить);
в) увеличь число в 100 раз: 57, 146, 90. Уменьши в 10 раз числа: 340, 500, 9800;
г) вычислить: 60 100+309, 9800:10-80;
д) сравни числа: 38000 и 3800.
Дополнительно к упражнениям учебника можно предложить следующие задания:
1. Запишите: а) 371 ед. в 1 классе; б) 90 ед. во 2 классе; в) 250 ед. во 2 классе; г) 8 ед. во 2 классе. Прочитать числа. Прочитать числа. Объяснить их состав.
2. Запишите числа и объясните их состав: двести пять тысяч шестьдесят четыре; двести двадцать семь тысяч шестьсот; триста тысяч семь; шесть миллионов пять тысяч три; пятьсот тысяч шесть и др.
Работа по изучению нумерации завершается отработкой навыков применения общей схемы разбора числа.
Изучение нумерации многозначных чисел завершается с ознакомление учащихся классами миллиардов и триллионов.
№ 16. Задачи на кратное отношение вводятся во 2 классе после усвоения формулировки правила: чтобы узнать, во сколько раз одно число больше или меньше, чем другое, надо большее число разделить на меньшее. Этот вывод делается после выполнения ряда упражнений вида: "В одном ряду 6 треугольников, а в другом 2 треугольника. Узнайте, во сколько раз треугольников в первом ряду больше, чем во втором?". Рассуждаем: разделим 6 треугольников по 2, получится 3 раза по 2, значит в первом ряду в 3 раза больше, чем во втором, а во втором в 3 раза меньше, чем в первом".
Дальнейшее решение задач на кратное отношение все время опирается на вышеупомянутое правило.
