1.Присчитывание и отсчитывание

Первым вычислительным приемом, который осваивает первоклассник, является прием вида a ± 1. Основой данного приема является принцип образования чисел в натуральном ряду: каждое следующее число на единицу больше предыдущего.

Усвоение ребенком этого принципа являлось центральной задачей изучения нумерации первого десятка.

Следствием этого принципа является способ нахождения значений выражений вида 5 + 1;8+1;6-1;7-1ит. п. путем называния либо следующего, либо предыдущего числа. Иными словами, для нахождения значения данных выражений нет необходимости выполнять какой-то прием арифметических действий, достаточно понимать, что добавление 1 ведет к получению следующего по счету числа, а убавление 1 — к появлению предыдущего по счету числа. Именно для получения результатов в таких выражениях ребенок заучивал наизусть названия чисел в прямом и обратном порядке.

Число предыдущее стоит в ряду чисел левее данного. При счете называется непосредственно перед данным, количественно оно содержит на одну единицу меньше данного.

Число последующее (следующее) стоит в ряду чисел правее дан­ного. При счете называется непосредственно после данного, количественно оно содержит на одну единицу больше данного.

Хорошее понимание принципа построения натурального ряда чисел ведет к легкому освоению приемов присчитывания и отсчитывания по 1 и легкому выполнению вычислительной деятель­ности в случаях:7 +1 17+1 177+1 10277+1 ; 7-1 17- 1 177- 1 10 277-1

Во всех случаях ссылка на принцип построения натуральной последовательности чисел является наиболее рациональной вплоть до 4 класса (общий прием вычислений):

— прибавляя к числу 1, получаем следующее по счету;

— вычитая из числа 1, получаем предыдущее по счету.

Использование линейки в качестве наглядной опоры для запоминания последовательности чисел, а также для усвоения способа нахождения числа последующего и предыдущего создает хорошие условия для интериоризации (усвоения образа во внутреннем плане, формирования наглядно представимой мысленной модели ряда натуральных чисел) способа нахождения результатов присчитывания и отсчитывания для детей с ведущим наглядно-образным мышлением.

Для детей с ведущим восприятием, требующим обязательной поддержки словесной информации мышечным усилием, двигательным действием, следует не только допускать, но и поощрять использование пальцевого счета при изучении всех вычислительных приемов первого десятка. Естественно, этот вариант внешнего подкрепления вычислительной деятельности является более медленным, многим учителям он кажется недопустимым для школьников, а потому старательно искореняется уже при обучении вычислениям в пределах первого десятка.

2.Прибавление и вычитание по частям

Следующую группу вычислительных приемов в пределах первого десятка составляют случаи вида: a ± 2, a ± 3, a ± 4, результаты которых могут быть найдены с помощью последовательного присчитывания или отсчитывания:2 + 3 = 2+1 + 1 + 1; 7-4 = 7-1-1-1-1 или с помощью прибавления и вычитания по частям:2 + 3 = 2+1 + 2; 7-4 = 7- 2- 2

Подготовительным приемом к обучению ребенка этим случаям вычислений является прием вида: а+1 + 1 и а-1-1, в основе которого лежит последовательное отсчитывание по 1 или присчитывание по 1.

Знакомство с этим приемом является очень важным.

Во-первых, осваивая данный вычислительный прием, ребенок впервые встречается с выражением, содержащим более одного знака действий.

При выполнении действий одной ступени без скобок, действия выполняются по порядку слева направо.

В-третьих, при выполнении данного вида вычислений не нужны специальные вычислительные действия какого-то нового вида, а требуется лишь последовательное применение принципа образования чисел в натуральном ряду.

Например: Вычислите 6+1 + 1. (Прибавляя к 6 единицу, получаем число следующее — это 7; прибавляя к 7 единицу, получаем следующее число — это 8. Значит, 6 + 1 + 1 = 8.)

В качестве наглядной модели удобно использовать линейку — прибавляя единицу дважды, ребенок делает вправо от числа 6 два «шага», получая ответ наглядно (на первых порах эти «шаги» полезно прослеживать пальцем).

Аналогично ребенок действует в случае вычислений вида а - 1 - 1. В этом случае используется понимание образования числа предыдущего к данному и знание последовательности чисел в обратном порядке.

Вычислительный прием а ± 2 является случаем, объединяющим последовательное присчитывание (отсчитывание) двух единиц к числу, производимое в предыдущем случае.

При прибавлении к любому числу двух, ребенок заменяет его на сумму двух единиц и последовательно присчитывает (отсчитывает) их от числа.

В качестве наглядной модели удобно использовать линейку — прибавляя два, ребенок делает вправо от числа два «шага», получая ответ наглядно.

М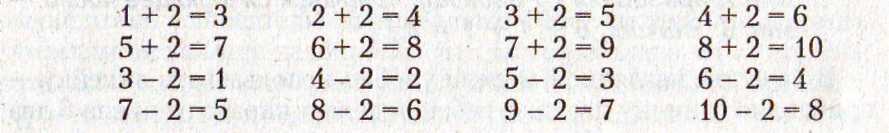 етодически ставится цель довести умение ребенка прибавлять и отнимать 2 до состояния навыка,

т. е. до запоминания результатов прибавления и вычитания двух в пределах 10 наизусть:

Таблица сложения и вычитания двух содержит самое большое количество случаев, а поскольку она изучается первой, многие дети испытывают большие трудности, пытаясь заучить этот объем.

Е сли при изучении чисел в пределах 10 (в разделе «нумерация в пределах 10»), ребенок выучил наизусть состав однозначных чисел и легко его воспроизводит, то проще всего для запоминания таблицы сложения и вычитания связать соответствующие случаи с составом однозначных чисел:

П ри опоре на состав числа имеет смысл сразу ориентировать ребенка на составление и запоминание тройки взаимосвязанных равенств:

Умение прибавлять и вычитать 2 является опорным умением для формирования дальнейшей вычислительной деятельности.

Вычислительные приемы а ± 3 и а ± 4 могут выполняться последовательным присчитыванием или отсчитыванием по 1:

8-4 = 8-1-1-1-1; 6 + 3 = 6+1 + 1 + 1

В этом случае используется ссылка на понятие числа предыдущего и последующего. Может быть использована линейка, по которой ребенок делает нужное количество «шагов» вправо или влево от заданного числа, или пальцевый счет. Методически этот способ считается менее совершенным, чем прибавление и вычитание по частям для данных вычислительных приемов.

Прибавление (или вычитание) по частям предполагает раскладывание второго слагаемого (или вычитаемого) на удобные для выполнения вычислений составные части, и последовательное их при­бавление (или вычитание):

Н апример: Приведенные примеры показывают, что с приемами а + 3 и а ± 4 легче справиться тем детям, которые помнят наизусть результаты случаев прибавления и вычитания двух, или могут достаточно быстро найти (вычислить) эти результаты.

Именно для освоения вычислений вида а + 3 и а + 4 предыдущую таблицу для случая а ± 2 учитель требовал заучивать наизусть.